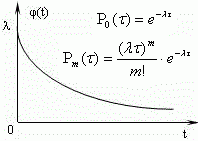Марковская цепь
Способы математических описаний марковских случайных процессов в системе с дискретными состояниями (ДС) зависят от того, в какие моменты времени (заранее известные или случайные) могут происходить переходы системы из состояния в состояние.Если переход системы из состояния в состояние возможен в заранее фиксированные моменты времени, имеем дело со случайным марковским процессом с дискретным временем. Если переход возможен в любой случайный момент времени, то имеем дело со случайным марковским процессом с непрерывным временем.
Пусть имеется физическая система S, которая может находиться в n состояниях S1, S2, …, Sn. Переходы из состояния в состояние возможны только в моменты времени t1, t2, …, tk, назовём эти моменты времени шагами. Будем рассматривать СП в системе S как функцию целочисленного аргумента 1, 2, …, k, где аргументом является номер шага.
Пример: S1 → S2 → S3 → S2.
Условимся обозначать Si(k) – событие, состоящее в том, что после k шагов система находится в состоянии Si.
При любом k события S1(k) , S2(k) ,…, Sn(k) образуют полную группу событий и являются несовместными.
Процесс в системе можно представить как цепочку событий.
Пример:S1(0), S2(1), S3(2), S5(3) ,….
Такая последовательность называется марковской цепью, если для каждого шага вероятность перехода из любого состояния Siв любое состояние Sjне зависит от того, когда и как система пришла в состояние Si.
Пусть в любой момент времени после любого k-го шага система S может находиться в одном из состояний S1, S2, …, Sn, т. е. может произойти одно событие из полной группы событий: S1(k), S2(k), …, Sn(k). Обозначим вероятности этих событий:
P1(1) = P(S1(1)); P2(1) = P(S2(1)); …; Pn(1) = P(Sn(k));
P1(2) = P(S1(2)); P2(2) = P(S2(2)); …; Pn(2) = P(Sn(2));
P1(k) = P(S1(k)); P2(k) = P(S2(k)); …; Pn(k) = P(Sn(k)).
Легко заметить, что для каждого номера шага выполняется условие
P1(k) + P2(k) +…+ Pn(k) = 1.
Назовём эти вероятности вероятностями состояний.следовательно, задача будет звучать следующим образом: найти вероятности состояний системы для любого k.
Пример.Пусть имеется какая-то система, которая может находиться в любом из шести состояний. тогда процессы, происходящие в ней, можно изобразить либо в виде графика изменения состояния системы (рис. 7.9, а), либо в виде графа состояний системы (рис. 7.9, б).
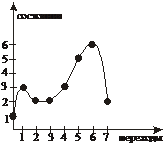
а)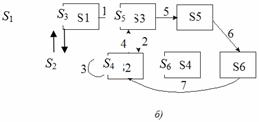 
Рис. 7.9
Также процессы в системе можно изобразить в виде последовательности состояний: S1, S3, S2, S2, S3, S5, S6, S2.
Вероятность состояния на (k + 1)-м шаге зависит только от состояния на k-м шаге.
Для любого шага k существуют какие-то вероятности перехода системы из любого состояния в любое другое состояние, назовем эти вероятности переходными вероятностями марковской цепи.
Некоторые из этих вероятностей будут равны 0, если переход из одного состояния в другое невозможен за один шаг.
Марковская цепь называется однородной, если переходные состояния не зависят от номера шага, в противном случае она называется неоднородной.
Пусть имеется однородная марковская цепь и пусть система S имеет n возможных состояний: S1, …, Sn. Пусть для каждого состояния известна вероятность перехода в другое состояние за один шаг, т.е. Pij (из Si в Sjза один шаг), тогда мы можем записать переходные вероятности в виде матрицы.
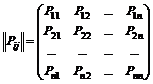. (7.1)
По диагонали этой матрицы расположены вероятности того, что система переходит из состояния Si в то же состояние Si.
Пользуясь введенными ранее событиями S1(k), S2(k),..., Sn(k) можно переходные вероятности записать как условные вероятности:
Pij=P(Sj(k)/Sik-1)
Очевидно, что сумма членов Pijk=P(Sj(k)/Sik-1) в каждой строке матрицы (1) равна единице, поскольку события S1(k), S2(k),..., Sn(k) образуют полную группу несовместных событий.
При рассмотрении марковских цепей, так же как и при анализе марковского случайного процесса, используются различные графы состояний (рис. 7.10).
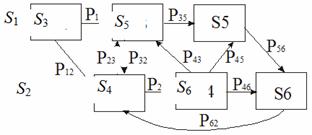
Рис. 7.10
Данная система может находиться в любом из шести состояний, при этом Pij – вероятность перехода системы из состояния Si в состояние Sj. Для данной системы запишем уравнения, что система находилась в каком-либо состоянии и из него за время t не вышла:
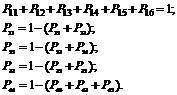
В общем случае марковская цепь является неоднородной, т. е. вероятность Pij меняется от шага к шагу. Предположим, что задана матрица вероятностей перехода на каждом шаге, тогда вероятность того, что система S на k-м шаге будет находиться в состоянии Si, можно найти по формуле
Зная матрицу переходных вероятностей и начальное состояние системы, можно найти вероятности состояний P1(k), P2(k), ..., Pn(k) после любого k-го шага. Пусть в начальный момент времени система находится в состоянии Sm. Тогда для t = 0
P1(0)=0, P2(0)=0,..., Pm(0)=1,..., Pn(0)=0
Найдем вероятности после первого шага. Из состояния Sm система перейдет в состояния S1, S2 и т.д. с вероятностями Pm1, Pm2, …, Pmm, … , Pmn. Тогда после первого шага вероятности будут равны
P1(1) = Pm1; P2(1) = Pm2, ..., Pn(1) = Pmn (7.2)
Найдем вероятности состояния после второго шага: P1(2), P2(2), ..., Pn(2). Будем вычислять эти вероятности по формуле полной вероятности с гипотезами:
.
Гипотезами будут следующие утверждения:
- после первого шага система была в состоянии S1-H1;
- после второго шага система была в состоянии S2-H2;
- после n-го шага система была в состоянии Sn-Hn.
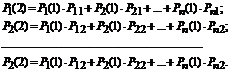
Вероятность любого состояния после второго шага:
(7.3)
В формуле (7.3) суммируются все переходные вероятности Pij, но учитываются только отличные от нуля. Вероятность любого состояния после k-го шага:
(7.4)
Таким образом, вероятность состояния после k-го шага определяется по рекуррентной формуле (7.4) через вероятности (k – 1)-го шага.
Задача 6. Задана матрица вероятностей перехода для цепи Маркова за один шаг. Найти матрицу перехода данной цепи за три шага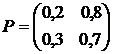
.
Решение. Матрицей перехода системы называют матрицу, которая содержит все переходные вероятности этой системы:
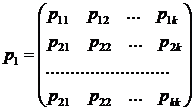
В каждой строке матрицы помещены вероятности событий (перехода из состояния i в состояние j), которые образуют полную группу, поэтому сумма вероятностей этих событий равна единице:
Обозначим через pij(n) вероятность того, что в результате n шагов (испытаний) система перейдет из состояния i в состояние j. Например p25(10) - вероятность перехода из второго состояния в пятое за десять шагов. Отметим, что при n=1 получаем переходные вероятности pij(1)=pij.
Перед нами поставлена задача: зная переходные вероятности pij, найти вероятности pij(n) перехода системы из состояния i в состояние j заn шагов. Для этого введем промежуточное (между iи j) состояние r. Другими словами, будем считать, что из первоначального состояния i за m шагов система перейдет в промежуточное состояние r с вероятностью pij(n-m), после чего, за оставшиеся n-m шагов из промежуточного состояния r она перейдет в конечное состояние j с вероятностью pij(n-m). По формуле полной вероятности получаем:
.
Эту формулу называют равенством Маркова. С помощью этой формулы можно найти все вероятности pij(n), а, следовательно, и саму матрицу Pn. Так как матричное исчисление ведет к цели быстрее, запишем вытекающее из полученной формулы матричное соотношение в общем виде Pn = P1n.
Вычислим матрицу перехода цепи Маркова за три шага, используя полученную формулу:
.
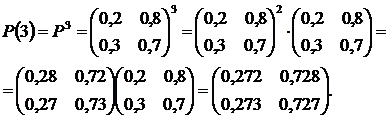
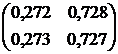Для проверка решения можно использовать калькулятор умножения матриц.
Задача №1. Матрица вероятностей перехода цепи Маркова имеет вид:
.
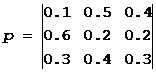Распределение по состояниям в момент времени t=0 определяется вектором:
π0=(0.5; 0.2; 0.3)
Найти:а) распределение по состояниям в моменты t=1,2,3,4.
в) стационарное распределение.
