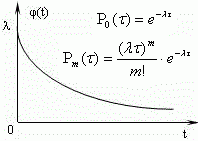Системы массового обслуживания
За последние десятилетия в самых разных областях народного хозяйства возникла необходимость решения вероятностных задач, связанных с работой систем массового обслуживания. Примерами таких систем служат телефонные станции, ремонтные мастерские, торговые предприятия, билетные кассы и т.д. работа любой системы массового обслуживания состоит в обслуживании поступающего в нее потока требований (вызовы абонентов, при ход покупателей в магазин, требования на выполнение работы в мастерской и т. д.).Математическая дисциплина, изучающая модели реальных систем массового обслуживания, получила название теории массового обслуживания. Задача теории массового обслуживания - установить зависимость результирующих показателей работы системы массового обслуживания (вероятности того, что требование будет обслужено; математического ожидания числа обслуженных требований и т. д.) от входных показателей (количество приборов в системе, параметров входящего потока требований и т. д.) установить такие зависимости в формульном виде можно только для простых систем массового обслуживания. Изучение же реальных систем проводится путем имитации, или моделирования их работы на ЭВМ с привлечением метода статистических испытаний.
Система массового обслуживания считается заданной, если определены:
1) входящий поток требований, или, иначе говоря, закон распределения, характеризующий моменты времени поступления требований в систему. Первопричину требований называют источником. В дальнейшем условимся считать, что источник располагает неограниченным числом требований и что требования однородны, т. е. различаются только моментами появления в системе;
2) система обслуживания, состоящая из накопителя и узла обслуживания. Последний представляет собой одно или несколько обслуживающих устройств, которые в дальнейшем будем называть приборами. Каждое требование должно поступить на один из приборов, чтобы пройти обслуживание. Может оказаться, что требованиям придется ожидать, пока приборы освободятся. В этом случае требования находятся в накопителе, образуя одну или несколько очередей. Положим, что переход требования из накопителя в узел обслуживания происходит мгновенно;
3) время обслуживания требования каждым прибором, которое является случайной величиной и характеризуется некоторым законом распределения;
4) дисциплина ожидания, т. е. совокупность правил, регламентирующих количество требований, находящихся в один и тот же момент времени в системе. Система, в которой поступившее требование получает отказ, когда все приборы заняты, называется системой без ожидания. Если требование, заставшее все приборы занятыми, становится в очередь и ожидает до тех пор,
пока освободиться один из приборов, то такая система называется чистой системой с ожиданием. Система, в которой требование, заставшее все приборы занятыми, становится в очередь только в том случае, когда число требований, находящихся в системе, не превышает определенного уровня (в противном случае происходит потеря требования), называется смешанной системой обслуживания;
5) дисциплина обслуживания, т. е. совокупность правил, в соответствии с которыми требование выбирается из очереди для обслуживания. Наиболее часто на практике используются следующие правила:
- заявки принимаются к обслуживанию в порядке очереди;
- заявки принимаются к обслуживанию по минимальному времени получения отказа;
- заявки принимаются к обслуживанию в случайном порядке в соответствии с заданными вероятностями;
6) дисциплина очереди, т.е. совокупность правил, в соответствии с которыми требование отдает предпочтение той или иной очереди (если их не сколько) и располагается в выбранной очереди. Например, поступившее требование может занять место в самой короткой очереди; в этой очереди оно может расположиться последним (такая очередь называется упорядоченной), а может пойти на обслуживание вне очереди. Возможны и другие варианты.
Классификация систем массового обслуживания
СМО могут быть двух видов:
♦ СМО с отказами;
♦ СМО с ожиданием (т. е. с очередью).
Обслуживание в системах с очередью может иметь различный характер:
Ø обслуживание может быть упорядоченным;
Ø обслуживание в случайном порядке;
Ø обслуживание с приоритетом, при этом приоритет может быть с прерыванием и без прерывания.
Системы с очередью делятся на:
- системы с неограниченным ожиданием, при этом поступившая в СМО задача становится в очередь и ждет обслуживания. Рано или поздно она будет обслужена;
- системы с ограниченным ожиданием, при этом на заявку в очереди накладываются ограничения, например ограниченное время пребывания в очереди, длина очереди, общее время пребывания в СМО. В зависимости от типа СМО для оценки эффективности могут быть применены разные показатели.
Для СМО с отказами используются следующие показатели эффективности:
- абсолютная пропускная способность А – среднее число заявок, которое может быть обслужено в единицу времени;
- относительная пропускная способность Q – относительное среднее число заявок. При этом относительную пропускную способность можно найти по формуле
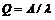
где λ – это интенсивность поступления заявок в СМО.
Для СМО с ожиданием абсолютная пропускная способность А и относительная пропускная способность Q теряют смысл, но важными становятся другие характеристики:
Ø единица времени ожидания в очереди;
Ø среднее число заявок в очереди;
Ø среднее время пребывания в системе.
Для СМО с ограниченной очередью интересны обе группы характеристик.
Имитационное моделирование систем массового обслуживания
Модель - это любой образ, аналог, мысленный или установленный, изображение, описание, схема, чертеж, и т. п. какого либо объекта, процесса или явления, который в процессе познания (изучения) замещает оригинал, сохраняя некоторые важные для данного исследования типичные свойства.Моделирование - это исследование какого-либо объекта или системы объектов путем построения и изучения их моделей. А также - это использование моделей для определения или уточнения характеристик и рационализации способов построения вновь конструируемых объектов.
Модель является средством для изучения сложных систем.
В общем случае сложная система представляется как многоуровневая конструкция из взаимодействующих элементов, объединяемых в подсистемы различных уровней. К сложным системам, в т.ч., относятся информационные системы. Проектирование таких сложных систем осуществляется в два этапа.
1 Внешнее проектирование
На этом этапе проводят выбор структуры системы, основных ее эле ментов, организация взаимодействия между элементами, учет воздействия внешней среды, оценка показателей эффективности системы.2 Внутреннее проектирование - проектирование отдельных элементов
системы
Типичным методом исследования сложных систем на первом этапе является моделирование их на ЭВМ.
В результате моделирования получаются зависимости, характеризующие влияние структуры и параметров системы на ее эффективность, надежность и другие свойства. Эти зависимости используются для получения оптимальной структуры и параметров системы.
Модель, сформулированная на языке математики с использованием математических методов называется математической моделью.
Для имитационного моделирования характерно воспроизведение явлений, описываемых математической моделью, с сохранением их логической структуры, последовательности чередования во времени. Для оценки искомых величин может быть использована любая подходящая информация, циркулирующая в модели, если только она доступна регистрации и последующей обработке.
Искомые величины при исследовании процессов методом имитационного моделирования обычно определяют как средние значения по данным большого числа реализаций процесса. Если число реализаций N, используемых для оценки искомых величин, достаточно велико, то в силу закона больших чисел получаемые оценки приобретают статистическую устойчивость и с достаточной для практики точностью могут быть приняты в качестве приближенных значений искомых величин.
Сущность метода имитационного моделирования применительно к задачам массового обслуживания состоит в следующем. Строятся алгоритмы,
при помощи которых можно вырабатывать случайные реализации заданных потоков однородных событий, а также моделировать процессы функционирования обслуживающих систем. Эти алгоритмы используются для много кратного воспроизведения реализации случайного процесса обслуживания при фиксированных условиях задачи. Получаемая при этом информация о состоянии процесса подвергается статистической обработке для оценки величин, являющихся показателями качества обслуживания
3 Формирование реализаций случайного потока заявок
При исследовании сложных систем методом имитационного моделирования существенное внимание уделяется учету случайных факторов.В качестве математических схем, используемых для формализации действия этих факторов, используются случайные события, случайные величины и случайные процессы (функции). Формирование на ЭВМ реализаций случайных объектов любой природы сводится к выработке и преобразованию случайных чисел. Рассмотрим способ получения возможных значений случайных величин с заданным законом распределения. Для формирования возможных значений случайных величин с заданным законом распределения исходным материалом служат случайные величины, имеющие равномерное распределение в интервале (0, 1). Другими словами, возможные значения xi случайной величины £, имеющей равномерное распределение в интервале (0, 1), могут быть преобразованы в возможные значения yi случайной величины г), закон распределения которой задан. Способ преобразования состоит в том, что из равномерно распределенной совокупности отбираются случайные числа, удовлетворяющие некоторому условию таким образом, чтобы отобранные числа подчинялись заданному закону распределения.
Предположим, что необходимо получить последовательность случайных чисел yi , имеющих функцию плотности 1^(у). Если область определения функции f^y) не ограничена с одной или обеих сторон, необходимо перейти к соответствующему усеченному распределению. Пусть область возможных значений для усеченного распределения равна (a, b).
От случайной величины г), соответствующей функции плотности f ^ y ), перейдем к f.
Случайная величина Ъ, будет иметь область возможных значений (0, 1) и функцию плотности f ^(z), задаваемую выражением.
Пусть максимальное значение f^(z) равно fm. Зададим равномерные распределения в интервалах (0, 1) случайных чисел x2i-1 и x2i. Процедура по лучения последовательности yi случайных чисел, имеющих функцию плотности ^(у), сводится к следующему:
1) из исходной совокупности выбираются пары случайных чисел x2i-1,
2) для этих чисел проверяется справедливость неравенства
х21<—— ^[а + (Ъ-а)х2М] (3)
m
3) если неравенство (3) выполнено, то очередное число yi определяется из соотношения
yi =a + (b-а)х21 (4)
При моделировании процессов обслуживания возникает необходимость формирования реализаций случайного потока однородных событий (заявок). Каждое событие потока характеризуется моментом времени tj, в который оно наступает. Чтобы описать случайный поток однородных событий как случайный процесс, достаточно задать закон распределения, характеризующий последовательность случайных величин tj. Для того, чтобы получить реализацию потока однородных событий t1, t2..., tk, необходимо сформировать реализацию zbz2,...,zk k-мерного случайного вектора ££2,..., Sk и вычислить значения ti в соответствии со следующими соотношениями:
t2 =
Пусть стационарный ординарный поток с ограниченным последействием задан функцией плотности f(z). В соответствии с формулой Пальма (6) найдем функцию плотности f1(z1) для первого интервала z1.
1- Jf ( u ) du
Теперь можно сформировать случайное число zb как было показано выше, соответствующее функции плотности f1(z1), и получить момент появления первой заявки t1 = z1. Далее формируем ряд случайных чисел, соответствующих функции плотности f(z), и при помощи соотношения (4) вычисляем значения величин t2, t3 ,.., tk.
4 Обработка результатов моделирования
При реализации моделирующих алгоритмов на ЭВМ вырабатывается информация о состояниях исследуемой системы. Эта информация является исходным материалом для определения приближенных значений искомых величин, или, как принято говорить, оценок для искомых величин.
Оценка вероятности события А вычисляется по формуле
p(A) = mN . (7)
Оценка среднего значения x случайной величины Ъ, вычисляется по
формуле
_ 1 n
k =1
Оценка S 2 для дисперсии случайной величины ^ вычисляется по формуле
1 N 1 ( N Л2
S 2 =1 YA xk 2—5> J (9)
Оценка корреляционного момента К^ для случайных величин Ъ, и ц с возможными значениями xk и yk соответственно вычисляется по формуле
1 N 1 NN
У>[Ух
5 Пример моделирования СМО
Рассмотрим следующую систему:
1 Требования поступают в случайные моменты времени, при этом
промежуток времени Q между любыми двумя последовательными требованиями имеет показательный закон с параметром i, т. е. функция распределения имеет вид
>0. (11)
Система обслуживания состоит из s одинаковых, пронумерованных приборов.
3 Время Тобсл - случайная величина с равномерным законом распределения на отрезке [a, b].
4 Система без ожидания, т.е. требование, заставшее все приборы занятыми, покидает систему.
5 Дисциплина обслуживания такова: если в момент поступления k - го требования первый прибор свободен, то он приступает к обслуживанию требования; если этот прибор занят, а второй свободен, то требование обслуживается вторым прибором, и т.д.
Требуется оценить математические ожидания числа требований, обслуженных системой за время Т и получивших отказ.
За начальный момент расчета выберем момент поступления первого требования Т1=0. Введем следующие обозначения: Тk- момент поступления k-го требования; ti - момент окончания обслуживания требования i-м прибором, i=1, 2, 3, ...,s.
Предположим, что в момент T 1 все приборы свободны.
Первое требование поступает на прибор 1. Время обслуживания этим прибором имеет равномерное распределение на отрезке [a, b].
Поэтому конкретное значение tобсл этого времени находим по формуле
(12)
где r- значение случайной величины R , равномерно распределенной на отрезке [0,1]. Прибор 1 будет занят в течение времени tобсл. Поэтому момент
времени
t
1 окончания обслуживания требования прибором
1 следует считать
равным:
t
1 = Т1+
t
о
бсл.
Затем следует добавить единицу в счетчик обслуженных требований и перейти к рассмотрению следующего требования.
Предположим, что k требований уже рассмотрено. Определим момент Тk+1 поступления (k+1)-го требования. Для этого найдем значение т промежутка времени
между последовательными требованиями. Так как этот про
межуток имеет показательный закон, то
12
х = — In r (13)
| Ll
где r -очередное значение случайной величины R . Тогда момент посту пления (k+1)-го требования: Т
k
+1 = Тк+Т.
Свободен ли в этот момент первый прибор? Для ответа на этот вопрос необходимо проверить условие
ti
<
Tk
+
i
- Если это условие выполнено, то к моменту Т
k
+1 первый прибор освободился и может
обслуживать требование.
В этом случае
t
1 заменяем на (Т
k
+1
+
t
обсл
), добавляем единицу в счетчик об
служенных
требований и переходим к следующему требованию. Если
t
1>Т
k
+1,
то первый
прибор в момент Т
k
+1 занят. В этом случае проверяем, свободен ли
второй прибор. Если условие
i
2<
Tk
+
i
выполнено, заменяем t2 на (Т
k
+1+
t
о
бсл),
добавляем единицу в счетчик обслуженных требований и переходим к
следующему требованию. Если
t
2>Т
k
+1, то проверяем условие 1з<Тк+1 и т. д.
Eсли
при всех
i
от 1 до
s
имеет
ti
>Т
k
+1, то в момент Т
k
+1 все приборы заняты. В этом
случае
прибавляем единицу в счетчик отказов и переходим к рассмотрению
следующего требования. Каждый раз, вычислив Т
k
+1, надо проверить еще ус
ловие окончания реализации:
Tk
+
i
<
T
. Если это условие выполнено, то одна
реализация
процесса функционирования системы воспроизведена и испыта
ние заканчивается. В счетчике обслуженных
требований и в счетчике отказов находятся
числа nобсл и nотк.
Повторив такое испытание n раз (с использованием различных r) и усреднив результаты опытов, определим оценки математических ожиданий
числа обслуженных требований и числа требований,
получивших отказ:
(14)
( Ji
n j =1
где ( nобсл ) j и ( nотк ) j - значения величин nобсл и nотк в
j
-ом опыте.
13
Список использованных источников
1 Емельянов А.А. Имитационное моделирование экономических процессов
[Текст]: Учеб. пособие для вузов / А.А. Емельянов, Е.А.
Власова, Р.В. Дума. -
М. : Финансы и статистика, 2002. - 368с.
2
Бусленко, Н.П. Моделирование сложных систем
[Текст]/ Н.П. Бусленко.-
М. : Наука, 1978. - 399с.
3
Советов Б.Я. Моделирование систем [Текст]:
Учеб. для вузов / Б.Я. Сове
тов, С.А. Яковлев. -М. : Высш. школа, 1985. - 271 с.
4
Советов Б.Я. Моделирование систем
[Текст]: Лабораторный практи
кум: Учеб. пособие для вузов по специальности:
"Автом. сист. обработ. инф.
и управл." / Б.Я. Советов, С.А. Яковлев. -М. :
Высш. шк., 1989. - 80 с.
5
Максимей И.В. Имитационное
моделирование на ЭВМ
[Текст]/
Максимей, И.В. -М : РАДИО И СВЯЗЬ, 1988. - 231с.
6
Вентцель Е.С. Теория вероятностей [ Текст ] :
учеб. для вузов / Е.С. Вент
цель.- М. : Высш. шк., 2001. - 575 с.
7
Гмурман, В.Е. Теория вероятностей
и математическая статисти
ка [ Текст ] : учеб. пособие / В.Е. Гмурман.- М. : Высш.
шк., 2001. - 479 с.
Приложение А
(обязательное)
Примерные темы расчетно-графических работ
1 На травмопункте работает один врач. Длительность лечения больного
и промежутки времени между поступлениями больных -
случайные величи
ны, распределенные по пуассоновскому закону.
По тяжести травм больные
делятся на три категории, поступление больного
любой категории - случай
ное событие с равновероятным распределением.
Врач вначале занимается
больными с максимально тяжелыми травмами (в
порядке их поступления),
затем, если таковых нет, больными средней
тяжести, и лишь затем - больны
ми с легкими травмами.
Смоделировать процесс и оценить средние времена
ожидания
в очереди больных каждой из категорий.
2 В городском автохозяйстве две ремонтные зоны. Первая обслуживает ремонты краткой и средней продолжительности, вторая - средней и долгой.
По мере поломок в автохозяйство доставляют транспорт; промежуток време ни между доставками - случайная пуассоновская величина. Продолжительности ремонта - случайная величина с нормальным законом распределения.
Смоделировать описанную систему. Оценить средние времена ожидания в очереди транспорта, требующие соответственно краткосрочного, среднесрочного и длительного ремонта.
3 Мини-маркет с одним контролером - кассиром обслуживает покупа телей, входящий поток которых подчиняется закону Пуассона с параметром 20 покупателей/час. Провести моделирование описанного процесса и определить вероятность простоя контролера - кассира среднюю длину очереди, среднее число покупателей в мини-маркете, среднее время ожидания обслуживания, среднее время пребывания покупателей в мини-маркете и дайте оценку его работы.
4 На АТС поступают заявки на междугородние переговоры. Поток зая вок является пуассоновским. В среднем за 1 час поступает 13 заявок.
Найдите среднее число заявок, поступающих за сутки, среднее время между появлением заявок. На телефонной станции появляются сбои в работе, если за полчаса на нее поступит более 50 заявок. Найдите вероятность сбоя станции.
5 На станцию технического обслуживания поступает простейший по
ток заявок с интенсивностью 1 автомобиль за 2 ч. Во дворе в очереди может находиться не более 3 машин. Среднее время ремонта - 2 часа. Дайте оценку работы СМО и разработайте рекомендации по улучшению обслуживания.
6 Одна ткачиха обслуживает группу станков, осуществляя по мере необходимости краткосрочное вмешательство, длительность которого - случайная величина. Смоделировать описанную ситуацию. Какова вероятность простоя сразу двух станков. Как велико среднее время простоя одного станка.
7 На междугородней телефонной станции две телефонистки обслуживают общую очередь заказов. Очередной заказ обслуживает та телефонистка, которая первой освободилась. Если обе в момент поступления заказа заняты, звонок аннулируется. Смоделировать процесс, считая входные потоки пуассоновскими.
8 На травмопункте работают два врача. Длительность лечения больно
го и промежутки времени между поступлениями
больных - случайные вели
чины, распределенные по
пуассоновскому закону. По тяжести травм больные
делятся на три категории, поступление
больного любой категории - случай
ное событие с равновероятным
распределением. Врач вначале занимается
больными с максимально тяжелыми
травмами (в порядке их поступления),
затем, если таковых нет, больными
средней тяжести, и лишь затем - больны
ми с легкими травмами. Смоделировать
процесс и оценить средние времена
ожидания в очереди больных каждой из
категорий.
9 На междугородней телефонной станции две телефонистки обслужи
вают общую очередь заказов. Очередной заказ обслуживает та телефонистка,
которая первой освободилась. Если обе в момент поступления заказа заняты,
то формируется очередь. Смоделировать процесс, считая входные потоки пу-
ассоновскими.
10
В системе передачи данных осуществляется
обмен пакетами данных
между узлами A и B по дуплексному каналу связи. Пакеты
поступают в
пункты
системы от абонентов с интервалами времени между ними 10 ± 3 мс.
Передача пакета занимает 10 мс. В пунктах имеются буферные регистры, ко
торые могут хранить два пакета, включая
передаваемый. В случае прихода
пакета в момент занятости регистров
пунктам системы предоставляется вы
ход на спутниковую полудуплексную
линию связи, которая осуществляет
передачу пакетов данных за 10 ± 5 мс. При занятости спутниковой линии па
кет получает отказ. Смоделировать обмен
информацией в системе передачи
данных в течение 1 мин. Определить
частоту вызовов спутниковой линии и
ее загрузку. В случае возможности
отказов определить необходимый для
безотказной работы системы объем
буферных регистров.
11
Пусть на телефонной станции с одним входом
используется обычная
система: если абонент занят, то очередь не формируется и
надо звонить сно
ва. Смоделировать ситуацию: три абонента пытаются дозвониться до одного
и того же владельца номера и в случае успеха
разговаривают с ним некоторое
(случайное по длительности) время. Какова вероятность
того, что некто, пы
тающийся дозвониться, не сможет это сделать за
определенное время Т.
12
Торговая фирма планирует выполнять заказы на
приобретение това
ров по телефону, для чего необходимо
установить соответствующую мини-
АТС с несколькими телефонными аппаратами. Если заказ
поступает, когда
все линии заняты, то клиент получает отказ. Если в момент
поступления за
явки
хотя бы одна линия свободна, то производится переключение на эту линию и
оформляется заказ. Интенсивность входящего потока заявок составляет 30 заказов
в час. Длительность оформления заявки в среднем равна 5 мин.
Определите оптимальное число каналов обслуживания,
чтобы обеспечить
условие стационарной работы СМО.
13
В магазине самообслуживание 6 контролеров - кассиров. Входящий
поток покупателей подчиняется закону
Пуассона с интенсивностью 120
чел/час. Один кассир может обслужить 40 человек в час. Определите вероят
ность простоя кассира, среднее число покупателей в
очереди, среднее время ожидания,
среднее число занятых кассиров. Дайте оценку работы СМО.
14. В магазин самообслуживания поступает
пуассоновский поток с ин
тенсивностью 200 покупателей в час. В течение
дня их обслуживают 3 кон
тролера-кассира с интенсивностью 90
покупателей в час. Интенсивность
входного потока
покупателей в часы пик возрастает до величины 400 поку
пателей в
час, а в часы спада достигает величины 100 покупателей в час. Определите
вероятность образования очереди в магазине и среднюю длину очереди в течение
дня, а также необходимое число контролеров-кассиров в часы пик и часы спада,
обеспечивающие такую же длину очереди и вероятность ее
образования, как и в номинальном режиме.
15. Среднее число покупателей, поступающих на узел расчета в магазин
самообслуживания 100 чел/час. Кассир может обслужить 60 человек в час.
Смоделируйте процесс и определите, какое число кассиров необходимо для того, чтобы вероятность появления очереди не превысила 0.6.
16. Провести моделирование очереди в магазине с одним продавцом при равновероятных законах распределения случайных величин: прихода по купателей и длительности обслуживания (при некотором фиксированном на боре параметров). Получить устойчивые характеристики: средние значения ожидания в очереди покупателем и простой продавца в ожидании прихода покупателей. Оценить их достоверность.
17. Провести моделирование очереди в магазине с одним продавцом при пуассоновских законах распределения случайных величин: прихода по купателей и длительности обслуживания (при некотором фиксированном на боре параметров). Получить устойчивые характеристики: средние значения ожидания в очереди покупателем и простой продавца в ожидании прихода покупателей. Оценить их достоверность.
18. Создайте модель бензоколонки. Найдите показатели качества обслуживания заявок. Определите количество стоек с тем, чтобы очередь не увеличивалась.
19. Среднее число покупателей, поступающих на узел расчета в магазин самообслуживания, 60 человек в час. Кассир может обслужить 35 человек в час. Смоделируйте процесс и определите, какое число кассиров необходимо для того, чтобы вероятность появления очереди не превысила 0.6.
20. Разработайте модель автобусного маршрута с n остановками. Определите показатели эффективности использования СМО.
Примеры
Задача №1. Дежурный по администрации города имеет один телефон. Телефонные звонки поступают с интенсивностью 90 заявок в час, средняя продолжительность разговора составляет 2 мин. Определить показатели СМО дежурного администратора.Примечание: выбираем λ = 90 в час.; t=2 мин.
Решение:
Исчисляем показатели обслуживания для одноканальной СМО:
Интенсивность потока обслуживания:
μ = 60/2 = 30
1. Интенсивность нагрузки.
ρ = λ • tобс = 90 • 2/60 = 3
Интенсивность нагрузки ρ=3 показывает степень согласованности входного и выходного потоков заявок канала обслуживания и определяет устойчивость системы массового обслуживания.
3. Вероятность, что канал свободен (доля времени простоя канала).
p0 = μ/(λ + μ)
p0 = 30(90 + 30) = 0.25
Следовательно, 25% в течение часа канал будет не занят, время простоя равно tпр = 15 мин.
4. Доля заявок, получивших отказ.
p1 = 1 - p0 = 1 - 0.25 = 0.75
Значит, 75% из числа поступивших заявок не принимаются к обслуживанию.
5. Относительная пропускная способность.
Доля обслуживаемых заявок, поступающих в единицу времени:
Q = p0 = 0.25
6. Абсолютная пропускная способность.
A = Q • λ = 0.25 • 90 = 22.5 заявок/час.
7. Среднее время простоя СМО.
tпр = pотк • tобс = 0.75 • 0.0333 = 0.02 час.
10. Среднее число обслуживаемых заявок.
Lобс = ρ • Q = 3 • 0.25 = 0.75 ед.
Число заявок, получивших отказ в течение час: λ • p1 = 68 заявок в час.
Номинальная производительность СМО: 1 / 0.0333 = 30 заявок в час.
Фактическая производительность СМО: 22.5 / 30 = 75% от номинальной производительности.
Пример №2. СМО представляет собой АЗС с n=5 колонками. Площадка возле АЗС позволяет ожидание в очереди не более m=2 машин. Поток автомашин на заправку простейший с интенсивностью λ = 35 машин в час. Среднее время заправки составляет 3 мин.
Решение:
Скачать решение
В магазине самообслуживания установлено, что поток покупателей является простейшим с интенсивностью λ = 1.95 покупателя в минуту. μ = 3 (t=0). Скачать решение
Пример №3. В отделении банка на обслуживании клиентов работают а1 операторов. Среднее время обслуживания одного клиента оператором а2 минуты банка. Определить характеристики работы банка и вероятность того, что не менее двух каналов простаивают. Как изменятся основные характеристики работы банка, если квалификация операторов такова, что позволяет каждому из них тратить на обслуживание одного клиента в среднем а4 минут?
Пример №4. В магазине самообслуживания установлено, что поток покупателей является простейшим с интенсивностью λ = 0.3 покупателя в минуту. μ = 2 (t=0).
В расчетном узле магазина самообслуживания работают 8 кассы. интенсивность входного потока составляет 0.0625 покупателей в минуту. интенсивность обслуживания каждого контролера-кассира составляет 0(t=72) покупателя минуту. Определить Вероятность отказа канала
Пример №5. Рассматривается круглосуточная работа пункта проведения профилактического осмотра автомашин с тремя каналами. На осмотр и выявления дефектов каждой машины затрачивается в середине 40 мин. На осмотр поступает в среднем 52 машины в сутки. Потоки заявок и обслуживаний простейшие. Если машина, прибывшая в пункт осмотра, не застает ни одного канала свободным, она уезжает. Найдите финальные вероятности, а также показатели эффективности рассматриваемой СМО.
Решите предыдущую задачу при условии неорганичной очереди и при условии двух заявок в очереди.
Решите предыдущую задачу при условии, что имеется четыре канала.
Определить число каналов обслуживания в задаче 1, чтобы относительная пропускная способность СМО была не менее 0,95.
Пример №6. Стол заказов магазина «Продукты» принимает заказы по двум телефонам. Среднее число поступающих заказов в течение часа – 80, среднее время оформления заказа – 3 минуты. Определите показатели системы массового обслуживания.
Методические рекомендации. Здесь n=2, λ = 80 в час, t = 3 мин. Перейти к решению.
Пример №7. Среднее число заказов такси, поступающих на диспетчерский пункт по двум телефонам в течение часа – 120. Среднее время оформления одного заказа – 4 минуты. Определите и дайте оценку показателям эффективности системы массового обслуживания.
Методические рекомендации. Здесь n=2, λ = 120 в час, t = 4 мин. Перейти к решению.