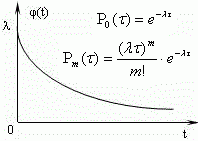Многоканальная СМО с ожиданиями
Рассмотрим многоканальную систему массового обслуживания с ожиданиями (число каналов равно n), в которой предусмотрены m мест в очереди на обслуживание. В СМО поступает поток заявок с интенсивностью λ. Интенсивность обслуживания μ одним каналом одной заявки также известна. Необходимо найти вероятности всех состояний системы и ее показатели эффективности.Пронумеруем состояния системы по числу заявок, связанных с системой, т. е. учитываем и заявки, которые уже обслуживаются, и заявки, которые только ожидают обслуживания, т. е. стоят в очереди:
- S0 – все каналы свободны и ни одной заявки не стоит в очереди;
- S1 – 1 канал занят, очереди нет;
- Sк – k каналов занято, очереди нет;
- Sn – n каналов занято, очереди нет;
- Sn+1 – n каналов занято, одна заявка стоит в очереди;
- Sn+m – n каналов занято, m заявок стоят в очереди.
Рис. 1
Таким образом, заявки будут поступать в систему массового обслуживания до тех пор, пока не будут заняты все каналы и все места в очереди. Если заявка прейдет в систему и застанет ее в состоянии Sn+m, то она покидает систему не обслуженной.
Определим показатели эффективности многоканальной СМО:
- вероятность того, что заявка получит отказ и покинет систему не обслуженной Ротк;
- абсолютную пропускную способность А;
- относительную пропускную способность Q;
- число занятых каналов k,
- среднее число заявок в очереди r,
- среднее число заявок, связанных с СМО, z.
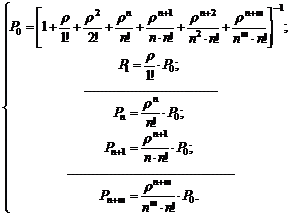 (38)
(38)
при этом ρ – это приведенная интенсивность, она равна отношению интенсивности поступления заявок λ к интенсивности обслуживания μ.
Вероятность отказа есть не что иное, как вероятность того, что поступившая в систему заявка найдет ее в состоянии Sn+m, т. е. все каналы и места в очереди заняты, следовательно, Ротк равна Pn+m, которую мы уже нашли [см. (38)].
![]() (39)
(39)
Событие, состоящее в том, что заявка, поступившая в систему, будет обслужена или хотя бы встанет в очередь на обслуживание, является противоположным событию Sn + m, следовательно, его вероятность будет равна
![]() (40)
(40)
Зная относительную пропускную способность системы, легко можно найти абсолютную пропускную способность по следующей формуле:
A = Q·λ (41)
Определим среднее число занятых каналов. Каждый канал в среднем в единицу времени обслуживает μ заявок. Вся СМО обслуживает А заявок, тогда
![]() . (42)
. (42)
Среднее число заявок в очереди можно вычислить непосредственно как математическое ожидание дискретной случайной величины, т. е.
![]()
![]() . (43)
. (43)
Среднее число заявок, связанных с системой, т. е. заявки, которые уже обслуживаются, и те, которые еще стоят в очереди и ждут обслуживания, получим как сумму числа занятых каналов k и среднего числа заявок в очереди r:
z=k + r (44)