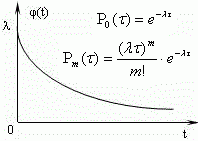СМО с отказами
Система ЭрлангаВ качестве показателей эффективности СМО с отказами будем рассматривать:
А — абсолютную пропускную способность СМО, т.е. среднее число заявок, обслуживаемых в единицу времени;
Q — относительную пропускную способность, т.е. среднюю долю пришедших заявок, обслуживаемых системой;
Pотк. — вероятность отказа, т.е. того, что заявка покинет СМО необслуженной;
Одноканальная система с отказами . Рассмотрим задачу.
Имеется один канал, на который поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ1. Найти предельные вероятности состояний системы и показатели ее эффективности.
Система S (СМО) имеет два состояния: S0 — канал свободен, S1 — канал занят. Размеченный граф состояний представлен на рис. 6.
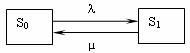
Рис. 6
В предельном, стационарном режиме система алгебраических уравнений для вероятностей состояний имеет вид.
![]()
![]() (18)
(18)
т.е. система вырождается в одно уравнение. Учитывая нормировочное условие p0+p1=1, найдем из (18) предельные вероятности состояний
![]() (19)
(19)
которые выражают среднее относительное время пребывания системы в состоянии S0 (когда канал свободен) и S1 (когда канал занят), т.е. определяют соответственно относительную пропускную способность Q системы и вероятность отказа Pотк:
![]() (20)
(20)
![]() (21)
(21)
Абсолютную пропускную способность найдем, умножив относительную пропускную способность Q на интенсивность потока отказов
![]() (22)
(22)
Задача 5. Известно, что заявки на телефонные переговоры в телевизионном ателье поступают с интенсивностью λ, равной 90 заявок в час, а средняя продолжительность разговора по телефону tоб.=2 мин. Определить показатели эффективности работы СМО (телефонной связи) при наличии одного телефонного номера.
Решение. Имеем λ=90 (1/ч), tоб.=2 мин. Интенсивность потока обслуживании μ=1/tоб=1/2=0,5 (1/мин)=30 (1/ч). По (20) относительная пропускная способность СМО (Q=30/(90+30)=0,25, т.е. в среднем только 25% поступающих заявок осуществят переговоры по телефону. Соответственно вероятность отказа в обслуживании составит Ротк.=0,75 (см. (21)).
Абсолютная пропускная способность СМО по (29) ,A=90∙0,25=22,5, т.е. в среднем в час будут обслужены 22,5 заявки на переговоры. Очевидно, что при наличии только одного телефонного номера СМО будет плохо справляться с потоком заявок.
Одноканальная СМО с отказами
Пусть в систему с одним каналом (n = 1) поступает пуассоновский поток с интенсивностью λ (в общем случае λ является функцией времени, т. е. λ = λ (t)). Заявка, заставшая канал занятым, получает отказ и покидает систему (рис. 22). Обслуживание в системе происходит в течение времени Тоб – это случайная величина, распределенная по показательному закону:F(t)=μ·e-μ·t (20)
Требуется найти:
- А – абсолютную пропускную способность СМО;
- Q – относительную пропускную способность СМО.
Рис. 22
Рассмотрим единственный канал обслуживания как физическую систему S, которая может находиться в двух состояниях:
S0 – канал свободен;
S1 – канал занят.
Поскольку события S0 и S1 образуют полную группу несовместных событий, то справедлива будет запись
Р0(t) + P1(t) = 1. (21)
Уравнения Колмогорова для данной системы массового обслуживания будут иметь вид
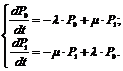 (22)
(22)
Из уравнения (21) выразим вероятность события, состоящего в том, что канал занят, в результате получим
Р1 = 1 – Р0. (23)
Подставим полученное выражение для Р1 в первое уравнение системы (22), тогда получается выражение вида
![]() .
.
Приведем подобные слагаемые для вероятности Р0:
![]() .
.
Тогда систему уравнений (22) можно записать в следующем виде:
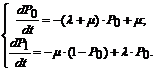 (24)
(24)
Начальными условиями будут:
- Р0(0) = 1, т. е. в начальный момент времени на входе СМО стоит заявка;
- Р1(0) = 0, при этом в начальный момент времени система свободна, следовательно, отказа не произойдет.
Проинтегрируем первое уравнение системы (24):
![]() .
.
Используя выражение (23), можно получить выражение для вычисления вероятности P1, т. е. вероятности того, что система занята. График поведения системы во времени показан на рис. 23.
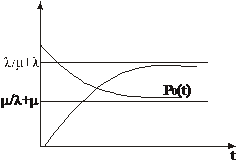
Рис. 23
После окончания переходного процесса при t→∞ вероятность Р0 будет вычисляться следующим образом: P0=M(λ+M) при t→∞.
Очевидно, что для одноканальной системы с отказами вероятность Р0 и есть относительная пропускная способность, которая рассчитывается таким образом:
Q = P0(t)=μ/(λ+μ), (25)
Зная Q, можно найти абсолютную пропускную способность А как произведение относительной пропускной способности Q на интенсивность поступления заявок λ, т. е.
А = λQ.
Подставим вместо Q выражение (25), следовательно,
A = λ·μ/(λ+μ).
Вероятность отказа есть не что иное, как средняя доля необслуженных заявок.
Ротк = 1 – Q,
при t→∞, Ротк = 1 – ![]() .
.
Пример. Пусть имеется телефонная линия, в которой интенсивность поступления заявок λ равна 0,8 вызовов/мин, время обслуживания одного разговора (заявки) tоб равно 1,5 мин. Требуется определить характеристики эффективности данной СМО.
Решение. Поскольку телефонная линия одна, система массового обслуживания относится к одноканальным СМО. Если очередная заявка, пришедшая в систему, находит систему занятой, то она получает отказ и покидает систему, следовательно, данная система является одноканальной СМО с отказами. Для данного вида СМО можно вычислить следующие характеристики:
- абсолютную пропускную способность А;
- относительную пропускную способность Q;
В первую очередь необходимо найти интенсивность обслуживания заявок в СМО μ. Для этого разделим единицу на время обслуживания одной заявки tоб
![]() .
.
Зная интенсивность поступления заявок в СМО λ и интенсивность обслуживания заявок в данной СМО μ, найдем относительную пропускную способность Q:
![]() .
.
Это значит, что в установившемся режиме система будет обслуживать 45,5 % проходящих заявок.
Теперь вычислим абсолютную пропускную способность СМО:
A=Q·λ = 0.364
Т. е. линия способна обслуживать в среднем 0,364 разговора в минуту.
Найдем вероятность отказа: единица минус относительная пропускная способность системы:
Ротк = 1 – Q = 0,545.
Вероятность того, что заявка, пришедшая в систему, найдет ее занятой, равна 54,5 %.
Кроме перечисленных выше характеристик можно также вычислить номинальную пропускную способность:
![]() .
.
Она равна 0,667 разговора в минуту, что в два раза превышает фактическую пропускную способность, полученную для случайного процесса.
Многоканальная система с отказами
Рассмотрим классическую задачу Эрланга.Имеется n каналов, на которые поступает поток заявок с интенсивностью λ. Поток обслуживаний имеет интенсивность μ. Найти предельные вероятности состояний системы и показатели ее эффективности.
Система S (СМО) имеет следующие состояния (нумеруем их по числу заявок, находящихся в системе): S0, S1, S2, …, Sk, …, Sn, где Sk — состояние системы, когда в ней находится k заявок, т.е. занято k каналов.
Граф состояний СМОсоответствует процессу гибели и размножения и показан на рис. 7.
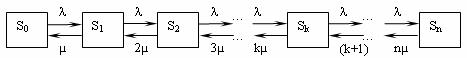
Поток заявок последовательно переводит систему из любого левого состояния в соседнее правое с одной и той же интенсивностью λ. Интенсивность же потока обслуживаний, переводящих систему из любого правого состояния в соседнее левое состояние, постоянно меняется в зависимости от состояния. Действительно, если СМО находится в состоянии S2 (два канала заняты), то она может перейти в состояние. S1 (один канал занят), когда закончит обслуживание либо первый, либо второй канал, т.е. суммарная интенсивность их потоков обслуживании будет 2μ. Аналогично суммарный поток обслуживаний, переводящий СМО из состояния S3 (три канала заняты) в S2. будет иметь интенсивность Зμ, т.е. может освободиться любой из трех каналов и т.д.
В формуле (16) для схемы гибели и размножения получим для предельной вероятности состояния
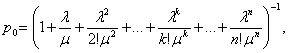 (23)
(23)
где члены разложения
называется приведенной интенсивностью потока заявок или интенсивностью нагрузки канала.Она выражает среднее число заявок, приходящее за среднее время обслуживания одной заявки. Теперь
p1=ρ·p0 (25)
Формулы (25) и (26) для предельных вероятностей получили названия формул Эрланга в честь основателя теории массового обслуживания.
Вероятность отказа СМО есть предельная вероятность того, что все n каналов системы будут заняты, т.е.
Относительная пропускная способность — вероятность того, что заявка будет обслужена:
Абсолютная пропускная способность:
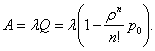 (29)
(29)
Среднее число занятых каналов k есть математическое ожидание числа занятых каналов:
где pk — предельные вероятности состояний, определяемых по формулам (25), (26).
Однако среднее число занятых каналов можно найти проще, если учесть, что абсолютная пропускная способность системы А есть не что иное, как интенсивность потока обслуженных системой заявок (в единицу времени). Так как каждый занятый канал обслуживает в среднем μ заявок (в единицу времени), то среднее число занятых каналов
или, учитывая (29), (24):
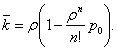 (31)
(31)