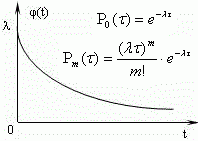Задание контрольной работы
1) Потребитель и его поведение. Для потребителя с функцией полезности u(x1,x2) :u(x1,x2)=x1 + x1x2/2 ;
P0=(1,2) ;
Q0=12 ;
k=2 ;
P3=3
1.записать математическую модель оптимального выбора потребителя
2. найти функции спроса на оба товара
3.найти точку спроса для цен P0 и дохода Q0 и дать содержательный ответ
4.пусть цена на товар k изменилась и стала равна Pk :
А)найти компенсацию дохода потребителя
Б)какой набор товаров является теперь оптимальным
В)сколько нужно средств, чтобы купить старый оптимальный набор по новой цене
Г)сравнить потребительские наборы
5.определить, на сколько % изменится спрос на товар k, если цена на другой товар увеличится на 1% при компенсации дохода.
2) Производитель и его поведение. Пусть производственная функция есть функция Кобба-Дугласа. Чтобы увеличить выпуск продукции на а%, надо увеличить основные фонды на b% или численность работников на с%. В настоящее время один работник за месяц производит продукции на М ден.ед., а численность работников- L. Основные фонды оцениваются в К ден.ед. а=1, b=3, с=3, M=104, L=103, K=105, N=3, D=10
Найти:
1. Производственную функцию фирмы
2. Величину средней фондоотдачи
3. Оптимальный размер фирмы, если период амортизации основных фондов – N месяцев, зарплата работника – D ден.ед. в месяц.
3) Модель межотраслевого баланса. Для условной экономики, состоящей из трех отраслей, известны коэффициенты прямых затрат аij
отрасли | аij | ||
1 | 2 | 3 | |
1 | 0 | 0,2 | 0 |
2 | 0,2 | 0 | 0,1 |
3 | 0 | 0,1 | 0,2 |
1.какой коэффициент продукт обеспечит валовой выпуск отраслей Xпл=(500,200,600)
2.найдите межотраслевые потоки и промежуточные продукты отраслей
3.по заданному плану непроизводственного потребления Упл=(200,100,300)
Исходные данные для своего варианта необходимо пересчитать по формулам:
(аij)3= аij + 0,005×3, (уi)3= уi + 10×3, (хi)3= хi + 10×3
Задачу решаем с помощью данного сервиса.
Скачать решение
4) Модели сетевого планирования и управления. В таблице для комплекса работ заданы очередность и порядок выполнения работ, длительность выполнения работ (в днях), количество исполнителей для каждой работы и имеющееся количество исполнителей R0 для всего комплекса работ. Требуется:
1.построить сетевой график для комплекса работ и пронумеровать события
2.рассчитать характеристики событий
3.определить, за какое минимальное время может быть выполнен весь комплекс работ
4.вычислить полные резервы времени работ
5.определить, на сколько дней можно отсрочить или растянуть во времени выполнение каждой работы, чтобы не изменилось общее время выполнения комплекса работ
6. построить линейный график работ и шкалу занятости исполнителей
8.вычислить, какое максимальное количество исполнителей требуется; равномерно ли исполнители загружены работой
9.пусть количество исполнителей равно R0 человек. При необходимости распределить исполнителей по работам так, чтобы время выполнения комплекса работ было как можно меньшим.
Событие (i) | Следующее за i событие (j) | Длительность работы t (i,j) | Количество исполнителей r (I,j) | R0 |
1 2 3 4 5 6 | 2,3 3,4,5 5 6 6 - | 5,1 2,2,3 8 1 1 - | 1,2 2,2,3 5 2 3 - | 5 |
Для решения применим сервис параметры сетевой модели. Выбираем количество равным 6 (начинать с вершины №1). Количество строк указываем – 8.
1→2 | 5 |
1→3 | 1 |
2→3 | 2 |
2→4 | 2 |
2→5 | 3 |
3→5 | 8 |
4→6 | 1 |
5→6 | 1 |
Также можно было ввести данные посредством матрицы расстояний.
Скачать решение
5) Системы массового обслуживания. Бригада рабочих из n человек обслуживает группу станков-автоматов, состоящую из m станков. Требования поступают на обслуживание в среднем с интенсивностью 2 станка в час. Обслуживание одного станка занимает у рабочего в среднем t минут. Необходимо определить:
А) среднее число станков, ожидающих обслуживания (среднюю длину очереди)
Б) коэффициент простоя станка
В) коэффициент простоя станка рабочего
Г)дать рекомендации по повышению эффективности работы системы и интерпретацию полученных ответов.
№ группы | 1,7 | 2,8 | 3,9 | 4,10 | 5,11 | 6,12 |
m | 6 | 8 | 10 | 15 | 12 | 16 |
n | 3 | 1 | 2 | 3 | 2 | 4 |
t | k | |||||
Где k=5N при N<5 ; k=N при 5≤N≤20 ; k=N/2 при N>20, (во всех случаях N=3)
Задача на многоканальные СМО. Выбираем λ = 2, μ = 1.5, m = 6, n =3.
Скачать решение
6) Статистические игры. Фирма планирует реализацию своей продукции на рынках, учитывая возможные варианты покупательского спроса Пj, j=1͞,4͞ (низкий, средний, высокий, очень высокий). На предприятии разработано три стратегии сбыта товаров A1, А2, А3. Объем товарооборота (ден.ед.), зависящий от стратегии и покупательского спроса, представлен в таблице.
Аj | Пj | |||
П1 | П2 | П3 | П4 | |
А1 | 30 +N | 10 | 20 | 25 + N/2 |
А2 | 50 | 70 - N | 10 + N/2 | 25 |
А3 | 25 – N/2 | 35 | 40 | 60 - N |
Где N=3
Известны возможные состояния покупательского спроса, которые соответственно q1=0,3, q2=0,2, q3=0,4, q4=0,1. Необходимо найти стратегию сбыта, максимизирующую средний товарооборот фирмы. При этом использовать критерии Вальда, Гурвица, Сэвиджа, Байеса.