Практикум по эконометрике
Линейное уравнение регрессии
Задание №1. По территориям Центрального района за 1995 г. имеются следующие данные:Y - средний размер назначенных ежемесячных пенсий, руб.;
Х - прожиточный минимум в среднем на одного пенсионера в месяц, руб., представленных в таблице 1.
Таблица 1. Данные за 1995 г. по территориям Центрального района
| Район | Средний размер назначенных ежемесячных пенсий, тыс. руб. У | Прожиточный минимум в среднем на одного пенсионера в месяц, тыс. руб. Х |
| Брянская область | 240 | 178 |
| Владимировская обл. | 226 | 202 |
| Ивановская обл. | 221 | 197 |
| Калужская обл. | 226 | 201 |
| Костромская обл. | 220 | 189 |
| г. Москва | 250+Ф | 302+И |
| Московская обл. | 237 | 215 |
| Орловская обл. | 232 | 166 |
| Рязанская обл. | 215 | 199 |
| Смоленская обл. | 220 | 180 |
| Тверская обл. | 222 | 181 |
| Тульская обл. | 231 | 186 |
| Ярославская обл. | 229+Ф | 250+И |
Выполнить следующий анализ связи между У и Х:
- построить поле корреляции и сформулировать гипотезу о форме связи,
- рассчитать по формулам коэффициенты линейного уравнения зависимости У от Х;
- оценить модель с помощью средней ошибки аппроксимации и критерия Фишера.
Пояснения. Все расчеты можно проверить с помощью функций Excel.
Перейти к онлайн решению своей задачи
Задание №2. В таблице 1 показаны месячные данные переменных деятельности фирмы по выпуску одного продукта:
У - объема выпуска продукции, тыс. руб.;
Х1 – время, месяцы;
Х2 – затраты на рекламу, тыс. руб.;
Х3 – цена продукции, тыс. руб.;
Х4 – цена конкурента, тыс. руб.;
Х5 индекс потребительских расходов.
Таблица 1. Варианты исходных данных для выполнения задания 2.1
| Время, месяцы, Х1 | Затраты на рекламу, тыс. руб., Х2 | Цена продукции, тыс. руб. Х3 | Цена продукции конкурента, тыс. руб. Х4 | Индекс потребительских расходов, Х5 | Объем выпуска продукции, тыс. руб. У |
| 1 | 4+0,1Ф | 15 | 17 | 100 | 126+И |
| 2 | 4,8 | 14,8 | 17,3 | 98,4 | 137 |
| 3 | 3,8 | 15,2 | 16,8 | 101,2 | 148 |
| 4 | 8,7 | 15,5 | 16,2 | 103,5 | 191 |
| 5 | 8,2 | 15,5+0,1Ф | 16 | 104,1 | 274 |
| 6 | 9,7 | 16 | 18 | 107 | 370 |
| 7 | 14,7 | 18,1 | 20,2 | 107,4 | 432+И |
| 8 | 18,7 | 13 | 15,8 | 108,5 | 445 |
| 9 | 19,8 | 15,8 | 18,2+0,1Ф | 108,3 | 367 |
| 10 | 10,6 | 16,9 | 16,8 | 109,2 | 367 |
| 11 | 8,6 | 16,3 | 17 | 110,1 | 321 |
| 12 | 6,5 | 16,1 | 18,3 | 110,7 | 307 |
| 13 | 12,6 | 15,4 | 16,4 | 110,3 | 331 |
| 14 | 6,5 | 15,7 | 16,2 | 111,8+0,1Ф | 345 |
| 15 | 5,8 | 16 | 17,7 | 112,3 | 364 |
| 16 | 5,7 | 15,1 | 16,2 | 112,9 | 384+И |
| 17 |
Где: Х1 – порядковый номер месяца: 1 – январь предыдущего года, 13- январь текущего года
Х5 - индекс потребительских расходов равен отношению значений потребительских расходов в текущем периоде к предыдущему;
Необходимо.
1. С помощью MS Excel программ Пакета анализа: Корреляция, Регрессия
- выполнить многофакторный анализ зависимости У от факторов Х1, Х2, Х3, Х4, Х5,
- получить прогнозные значения у по многофакторной модели.
Перейти к онлайн решению своей задачи
Задание №3. Основы регрессионного анализа.
1) Вычислить коэффициент корреляции
2) Составить линейное уравнение регрессии, описывающее выборочные данные.
3) Уточнить линейное уравнение регрессии. Для этого исключить из выборки несколько (не более 3) «плохих» точек.
4) Все результаты анализа представить графически и прогнозировать увеличение Y при увеличение X на 25% от заданного в таблице.
Решение проводят с использованием сервиса Линейное уравнение регрессии
. Для расчета параметров регрессии построим расчетную таблицу (табл. 1)
| x | y | x2 | y2 | x · y |
| 5.14 | 64.1 | 26.42 | 4108.81 | 329.47 |
| 9.5 | 60.5 | 90.25 | 3660.25 | 574.75 |
| 13.64 | 72.8 | 186.05 | 5299.84 | 992.99 |
| 15.12 | 80.5 | 228.61 | 6480.25 | 1217.16 |
| 16.68 | 82 | 278.22 | 6724 | 1367.76 |
| 18.24 | 94.2 | 332.7 | 8873.64 | 1718.21 |
| 19 | 112.1 | 361 | 12566.41 | 2129.9 |
| 22.6 | 108.5 | 510.76 | 11772.25 | 2452.1 |
| 23.5 | 120.2 | 552.25 | 14448.04 | 2824.7 |
| 25.78 | 110 | 664.61 | 12100 | 2835.8 |
| 26.68 | 121.4 | 711.82 | 14737.96 | 3238.95 |
| 28.12 | 134 | 790.73 | 17956 | 3768.08 |
| 224 | 1160.3 | 4733.43 | 118727.45 | 23449.88 |
Выборочные средние. x = ∑xi n = 224 12 = 18.67 y = ∑yi n = 1160.3 12 = 96.69 x·y = ∑xi·yi n = 23449.88 12 = 1954.16
Выборочные дисперсии: S2(x) = xi2 n - x2 = 4733.43 12 - 18.672 = 46.01 S2(y) = yi2 n - y2 = 118727.45 12 - 96.692 = 544.68
Среднеквадратическое отклонение S(x) = √ S2(x) = √ 46.01 = 6.78 S(y) = √ S2(y) = √ 544.68 = 23.34
Коэффициент корреляции b можно находить по формуле, не решая систему непосредственно: b = x·y - x·y S2(x) = 1954.16-18.67·96.69 46.01 = 3.2439
Рассчитываем показатель тесноты связи. Таким показателем является выборочный линейный коэффициент корреляции, который рассчитывается по формуле: rxy = x·y - x·y S(x)·S(y) = 1954.16-18.67·96.69 6.78·23.34 = 0.943
Линейный коэффициент корреляции принимает значения от –1 до +1.
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < rxy < 0.3: слабая;
0.3 < rxy < 0.5: умеренная;
0.5 < rxy < 0.7: заметная;
0.7 < rxy < 0.9: высокая;
0.9 < rxy < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X весьма высокая и прямая.
Уравнение регрессии (оценка уравнения регрессии). yx = rxy· x-x S(x) ·S(y)+y = 0.943· x-18.67 6.78 ·23.34+96.69 = 3.24·x+36.1
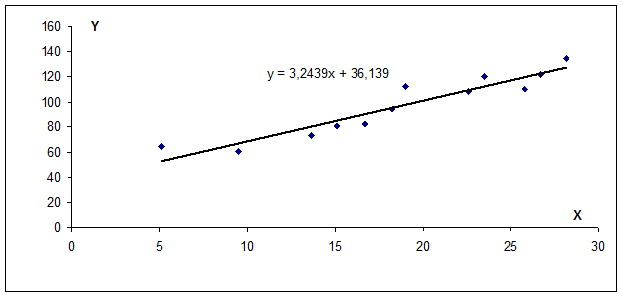
Линейное уравнение регрессии имеет вид y=3.24·x+36.14
Построим график.
Для расчета параметров регрессии построим расчетную таблицу (табл. 2)
| x | y | x2 | y2 | x·y |
| 9,5 | 60,5 | 90.25 | 3660.25 | 574.75 |
| 13,64 | 72,8 | 186.05 | 5299.84 | 992.99 |
| 15,12 | 80,5 | 228.61 | 6480.25 | 1217.16 |
| 16,68 | 82 | 278.22 | 6724 | 1367.76 |
| 18,24 | 94,2 | 332.7 | 8873.64 | 1718.21 |
| 22,6 | 108,5 | 510.76 | 11772.25 | 2452.1 |
| 23,5 | 120,2 | 552.25 | 14448.04 | 2824.7 |
| 25,78 | 110 | 664.61 | 12100 | 2835.8 |
| 26,68 | 121,4 | 711.82 | 14737.96 | 3238.95 |
| 28,12 | 134 | 790.73 | 17956 | 3768.08 |
| 199.86 | 984.1 | 4346.01 | 102052.23 | 20990.5 |
Выборочные средние. x = ∑xi n = 199.86 10 = 19.99 y = ∑yi n = 984.1 10 = 98.41 x·y = ∑xi·yi n = 20990.5 10 = 2099.05
Выборочные дисперсии: S2(x) = xi2 n - x2 = 4346.01 10 - 19.992 = 35.16 S2(y) = yi2 n - y2 = 102052.23 10 - 98.412 = 520.69
Среднеквадратическое отклонение S(x) = √ S2(x) = √ 35.16 = 5.93 S(y) = √ S2(y) = √ 520.69 = 22.82 rxy = x·y - x·y S(x)·S(y) = 2099.05-19.99·98.41 5.93·22.82 = 0.977
Коэффициент корреляции возрос.
Уравнение регрессии (оценка уравнения регрессии). yx = rxy· x-x S(x) ·S(y)+y = 0.977· x-19.99 5.93 ·22.82+98.41 = 3.76·x+23.25
Линейное уравнение регрессии имеет вид y=3.76·x+23.25
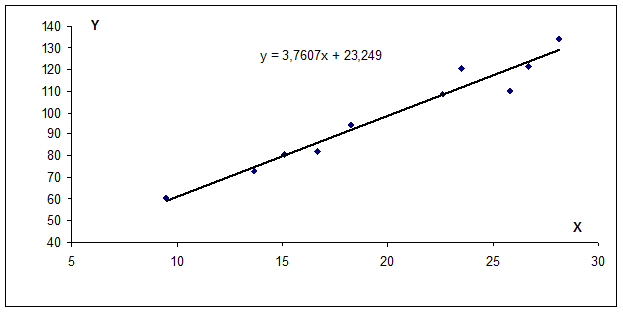
Сделаем прогноз.
Xp = 19.99 · 125% = 24.98
y(24.98) = 23.25 + 3.76*24.98 = 117.191