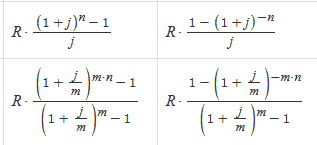Пример решения биматричной игры
Математической моделью конфликтов с двумя участниками являются биматричные игры. Такая игра 2х2 задается биматрицей (aij,bij) . В кооперативном варианте такой игры игроки могут согласованно выбирать элемент биматрицы. Если они выбрали элемент (a,b), то Первый игрок получает a , а Второй получает b . Цели игроков одинаковы - выиграть как можно больше в расчете на партию в среднем. Пусть (x,y), (a,b) - две точки из CE. Говорят, что (x,y) доминирует (a,b) если x≥a, y≥b и хотя бы одно из этих неравенств строгое. Недоминируемые точки называются оптимальными по Парето, а их множество - множеством оптимальности по Парето. Еще более узкое множество называется переговорным. Оно определяется так: пусть Vk - максимальный выигрыш, который k-й игрок может обеспечить себе при любой стратегии другого игрока, тогда переговорное множество определяется как множество тех точек множества Парето, у которых k-я координата не меньше Vk. Для нахождения Vk надо решить две задачи ЛП:V1→max, a11*x+a21*(1-x) ≥V1,a11*x+a12*(1-x)≥V1, 0≤x≤1;
V2→max, a11*y+a12*(1-y) ≥V2,a21*y+a22*(1-y)≥V2, 0≤y≤1.
Дано:
Биматрица
| 2 | 2 |
| 8 | 7 |
| 6 | 6 |
| 9 | 1 |
Нанесем на плоскость элементы биматрицы и начертим выпуклую оболочку.
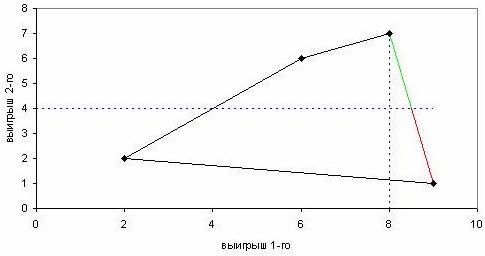
Графическое решение биматричной игры
Где красным и зеленым цветом обозначено множество оптимальности по Парето, а зеленым – та его часть, которая является переговорным множеством. V1=8, V2=4.
Цена игры первого игрока V1 находится легко, так как в матрице аij есть седловая точка а[2,1]=8. Основная теорема матричных игр утверждает, что для любой матричной игры max{min{M[P,Q]:Q}:P}=min{max{M[P,Q]:P}:Q}, т.е. во множестве смешанных стратегий есть седловая точка, дающая оптимальное решение игры. Поэтому V1= а[2,1]=8, а оптимальная стратегия 1-го игрока Р*=(0,1), так как ему выгодно выбирать все время 2-ю строку.
Для того, чтобы найти цену игры и оптимальную стратегию 2-го игрока необходимо решить задачу ЛП. Если все разделить на V2 и сделать замену переменных, то получим:
V2→max
y/V2=x1
x1 + x2 →min
2*y+6*(1-y)≥ V2, (1-y)/V2=x22*x1+6*x2≥1
7*y+1*(1-y) ≥V2, 7*x1 +1*x2≥1
0≤y≤1. x1, x2 ≥0
Решая ее находим V2=4.
Итак, цена игры 2-го игрока V2=4
Перейти к онлайн решению своей задачи
Пример. Найдите решения биматричной игры.
Решение находим с помощью калькулятора.
В каждом столбце матрицы A найдем максимальный элемент. Эти элементы подчеркнуты в матрице A. Их положение соответствует приемлемым ситуациям 1-го игрока, когда второй игрок выбрал стратегию j соответственно.
Затем в каждой строке матрицы B выберем наибольший элемент. Эти элементы подчеркнуты в матрице B. Их положение будет определять приемлемые ситуации 2-го игрока, когда первый игрок выбрал стратегию i соответственно.
Платежная матрица игрока А:
| -10 | 2 |
| 1 | -1 |
| 5 | -2 |
| -1 | 1 |
Если биматричная игра не имеет равновесных ситуаций в чистых стратегиях, то она неразрешима в чистых стратегиях. И тогда можно искать решение в смешанных стратегиях.
Итак, чтобы в биматричной игре:
А=(aij), В = (bij) пара (p,q);
определяемая равновесную ситуацию, необходимо и достаточно одновременное выполнение следующих неравенств:
(p–1)(Cq-α) ≥ 0, p(Cq-α) ≥ 0; 0 ≥ p ≥ 1
(q-1)(Dp-β) ≥ 0, q(Dp-β) ≥ 0; 0 ≥ q ≥ 1
где
C = a11 - a12 - a21 + a22
α = a22- a12
D = b11-b12-b21+b22
β = b22-b21
Проводя необходимые вычисления:
C = -10 - 2 - 1 -1 = -14
α = -1 - 2 = -3
D = 5 - (-2) - (-1) + 1 = 9
β = 1 - (-1) = 2
и рассуждения
(p–1)(-14q+3) ≥ 0
p(-14q+3) ≥ 0
(q-1)(9p-2) ≥ 0
q(9p-2) ≥ 0
получаем, что:
1) p=1,q ≥ 3/14
p=0, q ≤ 3/14
0 ≤ p ≤ 1, q=3/14
2) q=1,p ≥ 2/9
q=0, p ≤ 2/9
0 ≤ q ≤ 1, p=2/9
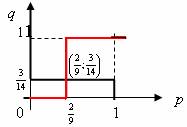
Цена игры
Ha(2/9;3/14) = -4/7
Hb(2/9;3/14) = 1/3
Ответ:
P* = (2/9;7/9); Q* = (3/14;11/14).
Выигрыш игроков в равновесной ситуации:
f(P*,Q*) = (-4/7;1/3).