Итерационный метод Брауна-Робинсона
Пусть игра задана матрицей A размерности m x n. Каждое разыгрывание игры в чистых стратегиях будет далее называться партией. Метод Брауна-Робинсон — это итеративная процедура построения последовательности пар смешанных стратегий игроков, сходящейся к решению матричной игры.В 1-ой партии оба игрока выбирают произвольную чистую стратегию. Пусть сыграно k партий, причем выбор стратегии в каждой партии запоминается. В (k + 1)-ой партии каждый игрок выбирает ту чистую стратегию, которая максимизирует его ожидаемый выигрыш, если противник играет в соответствии с эмпирическим вероятностным распределением, сформировавшимся за k партий. Оценивается интервал для цены игры и, если он достаточно мал, процесс останавливается. Полученные при этом вероятностные распределения определяют смешанные стратегии игроков.
Достоинства метода Брауна:
- Этот метод ориентирован на произвольную игру G(m×n).
- Не требует условия aij>0.
- Легко реализуем программными методами.
Недостатки метода Брауна: скорость сходимости метода быстро уменьшается с ростом размерности матрицы игры.
Рассмотрим метод на примере игры G(3×3).
| Ai \ Bj | B1 | B2 | B3 |
| A1 | 7 | 2 | 9 |
| A2 | 2 | 9 | 0 |
| A3 | 9 | 0 | 11 |
SB=(q1,q2,q3)
Строится следующая матрица:
| k | i | B1 | B2 | B3 | j | A1 | A2 | A3 | Vmin | Vmax | V* |
| 1 | 3 | 9 | 0 | 11 | 2 | 2 | 0 | 0 | 9 | 4.5 | |
| 2 | 2 | 11 | 9 | 11 | 2 | 4 | 0 | 4.5 | 9 | 6.75 | |
| 3 | 2 | 13 | 18 | 11 | 3 | 13 | 11 | 3.67 | 6 | 4.84 | |
| 4 | 2 | 13 | 18 | 11 | 3 | 18 | … | … | … | ||
| 5 | … | … | … | … | … | … | … | … | … | … | … |
| … | … | … | … | … | … | … | … | … | … | … | … |
k – номер партии.
i – номер стратегии, выбираемой игроком A.
j – номер стратегии, выбираемой игроком В.
Bi– накопленный игроком А выигрыш за k партий, при условии, что в данной партии B выбирает стратегию Bi.
Аj – накопленный игроком В проигрыш за k партий, при условии, что в данной партии A выбирает стратегию Аj.
Vmin – нижняя оценка игры = min (накопленный выигрыш)/k.
Vmax – верхняя оценка игры = max (накопленный проигрыш)/k.
Доказано, что
V*=(Vmin+Vmix)/2, V* à V при k à ¥ и
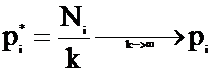
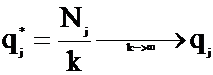
Ni - сколько раз выбирается Аi стратегия.
Nj - сколько раз выбирается Bj стратегия.
Итерационный процесс метода Брауна-Робинсон не является, вообще говоря, монотонным. Кроме того, скорость сходимости метода быстро уменьшается с ростом размерности матрицы игры. Однако он обладает одним неоспоримым преимуществом, которое заключается в исключительной простоте программирования метода.
Пример.
1. Проверяем, имеет ли платежная матрица седловую точку. Если да, то выписываем решение игры в чистых стратегиях.
Считаем, что игрок I выбирает свою стратегию так, чтобы получить максимальный свой выигрыш, а игрок II выбирает свою стратегию так, чтобы минимизировать выигрыш игрока I.
| Игроки | B1 | B2 | B3 | a = min(Ai) |
| A1 | 6 | 1 | 4 | 1 |
| A2 | 2 | 4 | 2 | 2 |
| A3 | 4 | 3 | 5 | 3 |
| b = max(Bi) | 6 | 4 | 5 |
Верхняя цена игры b = min(bj) = 4.
Что свидетельствует об отсутствии седловой точки, так как a ≠ b, тогда цена игры находится в пределах 3 <= y <= 4. Находим решение игры в смешанных стратегиях. Объясняется это тем, что игроки не могут объявить противнику свои чистые стратегии: им следует скрывать свои действия. Игру можно решить, если позволить игрокам выбирать свои стратегии случайным образом (смешивать чистые стратегии).
| k | i | B1 | B2 | B3 | j | A1 | A2 | A3 | Vmin | Vmax | Vср |
| 1 | 1 | 6 | 1 | 4 | 2 | 1 | 4 | 3 | 1 | 4 | 5/2 |
| 2 | 2 | 8 | 5 | 6 | 2 | 2 | 8 | 6 | 5/2 | 4 | 13/4 |
| 3 | 2 | 10 | 9 | 8 | 3 | 6 | 10 | 11 | 8/3 | 11/3 | 19/6 |
| 4 | 3 | 14 | 12 | 13 | 2 | 7 | 14 | 14 | 3 | 7/2 | 13/4 |
| 5 | 2 | 16 | 16 | 15 | 3 | 11 | 16 | 19 | 3 | 19/5 | 17/5 |
| 6 | 3 | 20 | 19 | 20 | 2 | 12 | 20 | 22 | 19/6 | 11/3 | 41/12 |
| 7 | 3 | 24 | 22 | 25 | 2 | 13 | 24 | 25 | 22/7 | 25/7 | 47/14 |
| 8 | 3 | 28 | 25 | 30 | 2 | 14 | 28 | 28 | 25/8 | 7/2 | 53/16 |
| 9 | 2 | 30 | 29 | 32 | 2 | 15 | 32 | 31 | 29/9 | 32/9 | 61/18 |
| 10 | 2 | 32 | 33 | 34 | 1 | 21 | 34 | 35 | 16/5 | 7/2 | 67/20 |
| 11 | 3 | 36 | 36 | 39 | 1 | 27 | 36 | 39 | 36/11 | 39/11 | 75/22 |
| 12 | 3 | 40 | 39 | 44 | 2 | 28 | 40 | 42 | 13/4 | 7/2 | 27/8 |
| 13 | 3 | 44 | 42 | 49 | 2 | 29 | 44 | 45 | 42/13 | 45/13 | 87/26 |
| 14 | 3 | 48 | 45 | 54 | 2 | 30 | 48 | 48 | 45/14 | 24/7 | 93/28 |
| 15 | 2 | 50 | 49 | 56 | 2 | 31 | 52 | 51 | 49/15 | 52/15 | 101/30 |
| 16 | 2 | 52 | 53 | 58 | 1 | 37 | 54 | 55 | 13/4 | 55/16 | 107/32 |
| 17 | 3 | 56 | 56 | 63 | 1 | 43 | 56 | 59 | 56/17 | 59/17 | 115/34 |
| 18 | 3 | 60 | 59 | 68 | 2 | 44 | 60 | 62 | 59/18 | 31/9 | 121/36 |
| 19 | 3 | 64 | 62 | 73 | 2 | 45 | 64 | 65 | 62/19 | 65/19 | 127/38 |
| 20 | 3 | 68 | 65 | 78 | 2 | 46 | 68 | 68 | 13/4 | 17/5 | 133/40 |
P(A1) = 1/20 = 1/20
NA2 = 7
P(A2) = 7/20 = 7/20
NA3 = 12
P(A3) = 12/20 = 3/5
NB1 = 4
P(B4) = 4/20 = 1/5
NB2 = 14
P(B4) = 14/20 = 7/10
NB3 = 2
P(B4) = 2/20 = 1/10
Цена игры, W = 133/40
p = (1/20, 7/20, 3/5)
q = (1/5, 7/10, 1/10)