Формализация игры. Матрица игры

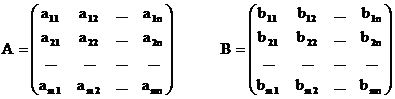
Итак, математической моделью антагонистической игры является матричная игра с матрицей A, в которой ходы (стратегии) игрока A расположены по строкам, а ходы (стратегии) игрока B расположены по столбцам. В самой матрице записаны выигрыши игрока A при соответствующих ходах игроков A и B (отрицательный выигрыш - это проигрыш).

Пример 1. Рассмотрим антагонистическую игру, в которой участвуют два игрока, каждый из которых имеет две стратегии. Выигрыши каждого из игроков определены следующими правилами: если оба из игроков выбирают стратегии с одинаковыми номерами, то первый выигрывает одну условную единицу. Если игроки выбирают разные стратегии, то выигрывает второй игрок условную единицу. В этом случае платёжная матрица имеет вид:
А =

Пример 2. Игроки A и B играют в следующую игру. Игрок A записывает одно из чисел 6, 7, 9, а игрок B записывает одно из чисел 4, 5. Если сумма чисел четная, то это выигрыш игрока А. Если сумма чисел нечётная, то это выигрыш игрока В (проигрыш игрока А). Найти платёжную матрицу игры А.
Имеем три стратегии первого игрока. А₁ = 6, А₂ = 7, А₃ = 9, В₁ = 4, В₂ = 5. Матрица игры:
А =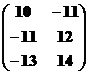

Оптимальные стратегии

Определение 1. Нижней ценой игры V_* называется величина, являющаяся максиминным значением платёжной матрицы:
V_* = max min a_ij
(сначала находится минимум в каждой строке, а затем из полученных минимумов находят максимум). Нижняя цена игры - это гарантированный выигрыш первого игрока А при любой стратегии игрока В.

Определение 2. Верхней ценой игры V^* называется величина, являющаяся минимаксным значением платёжной матрицы:
V^* = min max a_ij
(сначала находится максимум в каждом столбце, а затем из полученных максимумов находят минимум). Верхняя цена игры - это гарантированный проигрыш второго игрока B при любой стратегии игрока A.
В силу того, что игра антагонистическая, всегда V_* ≤ V^*. Если V_* = V^* = V, то просто говорят о цене игры, такая игра называется вполне определённой, игрой с седловой точкой, поскольку значение элемента платёжной матрицы, равное V = V_* = V^* является минимальным в своей строке и максимальным в своём столбце. Соответствующие этой цене игры стратегии называются оптимальными, поскольку второй игрок не может понизить нижнюю цену игры, а первый игрок не может повысить верхнюю цены игры.

Пример 3. Платёжная матрица игры:
А = .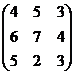

Определим, существует ли седловая точка. Для этого находим минимум в каждой строке матрицы. Минимальным числом в первой строке будет 3, во второй -- 4 и в третьей -- 2. Из полученных минимумов находим максимум:
V_* = max(3,4,2) = 4
Находим максимум в каждом столбце. Это числа 6, 7, 4 соответственно. Из полученных максимумов находим минимум:
V^* = min(6,7,4) = 4
Следовательно, исходя из данного выше определения цены игры, в данном случае цена игры V = V_* = V^* = 4, седловая точка существует, и это есть элемент платёжной матрицы a₂₃ = 4. Ей соответствуют единственная оптимальная стратегии - A₂ первого игрока и единственная оптимальная стратегия - B₃ второго игрока.
В общем случае в игре может быть несколько седловых точек и, следовательно, несколько оптимальных стратегий (решений) игровой задачи.

Пример 4. Задана платёжная матрица игры, необходимо найти оптимальное решение игры.
А =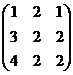
Определим, существует ли седловая точка. Для этого находим минимумы в каждой строке матрицы. Минимальным числом в первой строке будет 1, во второй это 2 и в третьей тоже 2. Из полученных минимумов находим максимум:
V_* = max(1,2,2) = 2
Находим максимум в каждом столбце. Это числа 4, 2, 2 соответственно. Из полученных максимумов находим минимум:
V^*=min(4,2,2) = 2
Следовательно, исходя из данного выше определения цены игры, в данном случае цена игры V = V_* = V^* = 2. Ей соответствуют стратегии A₂ , А₄ первого игрока, и стратегии В₂, B₃второго игрока (так как a₂₂= а₂₃ = а₃₂ = а₃₃ = 2). Из приведённого анализа следует, что в рассматриваемой платёжной матрице A существуют четыре седловых точек a₂₂ , а₂₃ , а₃₂ , а₃₃, поскольку каждый из этих элементов является минимальным элементом в своей строке и максимальным элементом в своём столбце.
Данная игра будет иметь четыре оптимальных решения, которыми являются следующие пары стратегий:

• 2-я стратегия первого игрока и 2-я стратегия второго игрока, которым соответствует элемент а₂₂;
• 2-я стратегия первого игрока и 3-я стратегия второго игрока, которым соответствует элемент а₂₃;
• 3-я стратегия первого игрока и 2-я стратегия второго игрока, которым соответствует элемент а₃₂;
• 3-я стратегия первого игрока и 3-я стратегия второго игрока, которым соответствует элемент а₃₃.

Пример 5. Задана платёжная матрица игры A, необходимо найти решение игры.
A =
В данной игре
V_* = max (min a_ij)= 3a_ij

V^* = min (max a_ij) = 4
Поскольку V_* < V^* - выполняется соотношение строгого неравенства, следовательно, седловая точка в игре отсутствует, ситуации равновесия не существует. Очевидно, что для данной игры рассмотренный выше подход к нахождению оптимального решения неприменим, а максиминная и минимаксная стратегия игроков не являются решением игры.

Приведённые выше примеры иллюстрируют тот факт, что антагонистические игры делятся на два класса:

1. вполне определённые игры, т.е. те, в которых существует седловая точка, ситуация равновесия и решение игры в чистых стратегиях;
2. не вполне определенные игры, т.е. те, в которых не существует седловой точки, ситуации равновесия и решения игры в чистых стратегиях. Для не вполне определённых игр принцип решения в той форме, для которой он изложен для вполне определённых игр, неприменим.