Задача принятия решений в условиях неопределенности
Предположим, что ЛПР (лицо, принимающее решения) рассматривает несколько возможных решений: i = 1,…,m. Ситуация, в которой действует ЛПР, является неопределенной. Известно лишь, что наличествует какой-то из вариантов: j = 1,…, n. Если будет принято i-e решение, а ситуация есть j-я , то фирма, возглавляемая ЛПР, получит доход qij. Матрица Q = (qij) называется матрицей последствий (возможных решений). Какое же решение нужно принять ЛПР? В этой ситуации полной неопределенности могут быть высказаны лишь некоторые рекомендации предварительного характера. Они не обязательно будут приняты ЛПР. Многое будет зависеть, например, от его склонности к риску. Но как оценить риск в данной схеме?Допустим, мы хотим оценить риск, который несет i-e решение. Нам неизвестна реальная ситуация. Но если бы ее знали, то выбрали бы наилучшее решение, т.е. приносящее наибольший доход. Т.е. если ситуация есть j-я , то было бы принято решение, дающее доход qij.
Значит, принимая i-e решение мы рискуем получить не qj, а только qij, значит принятие i-го решения несет риск недобрать rij = qj - qij. Матрица R = (rij) называется матрицей рисков.
Пример №1. Пусть матрица последствий есть
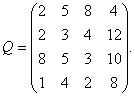
Составим матрицу рисков. Имеем q1 = max(qi1) = 8, q2 = 5, q3 = 8, q4 = 12.. Следовательно, матрица рисков есть
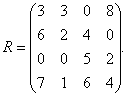
Принятие решений в условиях полной неопределенности
Не все случайное можно "измерить" вероятностью. Неопределенность – более широкое понятие. Неопределенность того, какой цифрой вверх ляжет игральный кубик отличается от неопределенности того, каково будет состояние российской экономики через 15 лет. Кратко говоря, уникальные единичные случайные явления связаны с неопределенностью, массовые случайные явления обязательно допускают некоторые закономерности вероятностного характера.Ситуация полной неопределенности характеризуется отсутствием какой бы то ни было дополнительной информации. Какие же существуют правила-рекомендации по принятию решений в этой ситуации?
Правило Вальда (правило крайнего пессимизма). Рассматривая i-e решение будем полагать, что на самом деле ситуация складывается самая плохая, т.е. приносящая самый малый доход ai Но теперь уж выберем решение i0 с наибольшим ai0. Итак, правило Вальда рекомендует принять решение i0, такое что ![]()
Так, в вышеуказанном примере, имеем a1 = 2, a2 = 2, a3 = 3, a4 = 1. Из этих чисел максимальным является число 3. Значит, правило Вальда рекомендует принять 3-е решение.
Правило Сэвиджа (правило минимального риска). При применении этого правила анализируется матрица рисков R = (rij). Рассматривая i-e решение будем полагать, что на самом деле складывается ситуация максимального риска bi = max [rij]
Но теперь уж выберем решение i0 с наименьшим bi0. Итак, правило Сэвиджа рекомендует принять решение i0, такое что ![]()
В рассматриваемом примере имеем b1 = 8, b2 = 6, b3 = 5, b4 = 7. Минимальным из этих чисел является число 5. Т.е. правило Сэвиджа рекомендует принять 3-е решение.
Правило Гурвица (взвешивающее пессимистический и оптимистический подходы к ситуации). Принимается решение i, на котором достигается максимум
![]() , где
, где 0 ≤ λ ≤ 1.
Значение λ выбирается из субъективных соображений. Если λ приближается к 1, то правило Гурвица приближается к правилу Вальда, при приближении λ к 0, правило Гурвица приближается к правилу "розового оптимизма" (догадайтесь сами, что это значит). В вышеуказанном примере при λ= 1/2 правило Гурвица рекомендует 2-е решение.
Принятие решений в условиях частичной неопределенности
Предположим, что в рассматриваемой схеме известны вероятности pj того, что реальная ситуация развивается по варианту j. Именно такое положение называется частичной неопределенностью. Как здесь принимать решение? Можно выбрать одно из следующих правил.Правило максимизации среднего ожидаемого дохода. Доход, получаемый фирмой при реализации i-го решения, является случайной величиной Qi с рядом распределения
qi1 | qi2 | … | qin |
p1 |
p2 | … |
pn |
Математическое ожидание M[Qi] и есть средний ожидаемый доход, обозначаемый
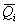 . Правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.
. Правило рекомендует принять решение, приносящее максимальный средний ожидаемый доход.
Предположим, что в схеме из предыдущего примера вероятности есть (1/2, 1/6, 1/6, 1/6). Тогда Q1=29/6, Q2=25/6, Q3=7, Q4=17/6. Максимальный средний ожидаемый доход равен 7, соответствует третьему решению.
Правило минимизации среднего ожидаемого риска. Риск фирмы при реализацииi-го решения, является случайной величиной Riс рядом распределения
ri1 | ri2 | … | rin |
p1 |
p2 | … |
pn |
Математическое ожидание M[Ri] и есть средний ожидаемый риск, обозначаемый также Ri. Правило рекомендует принять решение, влекущее минимальный средний ожидаемый риск.
Вычислим средние ожидаемые риски при указанных выше вероятностях. Получаем R1=20/6, R2=4, R3=7/6, R4=32/5. Минимальный средний ожидаемый риск равен 7/6, соответствует третьему решению.
Анализ принимаемых решений по двум критериям: среднему ожидаемому доходу и среднему ожидаемому риску и нахождение решений, оптимальных по Парето, аналогично анализу доходности и риска финансовых операций. В примере множество решений, оптимальных по Парето операций, состоит только из одного 3-его решения.
В случае, если количество Парето-оптимальных решений больше одного, то для определения лучшего решения применяется взвешивающая формула f(Q)=2Q-R.
Правило Лапласа
Иногда в условиях полной неопределенности применяют правило Лапласа, согласно которому все вероятности pj считают равными. После этого можно выбрать какое-нибудь из двух приведенных выше правил-рекомендаций принятия решений.Пример №2. Рассмотрим пример решения статистической игры в экономической задаче.
Сельскохозяйственное предприятие может реализовать некоторую продукцию:
А1) сразу после уборки;
А2) в зимние месяцы;
А3) в весенние месяцы.
Прибыль зависит от цены реализации в данный период времени, затратами на хранение и возможных потерь. Размер прибыли, рассчитанный для разных состояний-соотношений дохода и издержек (S1, S2 и S3), в течение всего периода реализации, представлен в виде матрицы (млн. руб.)
| S1 | S2 | S3 | |
| A1 | 2 | -3 | 7 |
| A2 | -1 | 5 | 4 |
| A3 | -7 | 13 | -3 |
Решение
Результаты расчетов будем заносить в таблицу:
| S1 | S2 | S3 | Б | НО | ММ | П-О | Х-Л | |
| А1 | 2 | -3 | 7 | 1 | 2 | -3 | 3 | -0,6 |
| А2 | -1 | 5 | 4 | 3,5 | 2,7 | -1 | 2,6 | 1,7 |
| А3 | -7 | 13 | -3 | 4,2 | 1 | -7 | 5 | -0,28 |
| pj | 0,2 | 0,5 | 0,3 | А3 | А2 | А2 | А3 | А2 |
1. Критерий Байеса (максимального математического ожидания)
Расчет осуществляется по формуле:W1 = 2∙0,2 + (-3) ∙0,5 + 7∙0,3 = 0,4 – 1,5 + 2,1 = 1
W2 = -1∙0,2 + 5 ∙0,5 + 4∙0,3 = -0,2 + 2,5 + 1,2 = 3,5
W3 = -7∙0,2 + 13 ∙0,5 + (-3)∙0,3 = -1,2 + 6,5 - 0,9 = 4,2
Найденные значения заносим в первый столбец (Б) и выбираем максимальное
W = max{1;3.5;4.2} = 4.2,
значит оптимальной по данному критерию является стратегия А3 – продавать в весенние месяцы.
2. Критерий недостаточного основания Лапласа (НО)
Находим среднее значение элементов каждой строки:Найденные значения заносим во второй столбец (НО) и выбираем максимальное W = max{2; 2.7; 1} = 2.7, значит оптимальной по данному критерию является стратегия А2 – продавать в зимние месяцы.
3. Максиминный критерий Вальда (ММ)
В каждой строке находим минимальный элемент:W1 = min{2; -3; 7} = -3
W2 = min{-1; 5; 4} = -1
W3 = min{-7; 13; -3} = -7
Найденные значения заносим в третий столбец (ММ) и выбираем максимальное W= max{-3; -1; -7} = -1, значит оптимальной по данному критерию является стратегия А2 – продавать в зимние месяцы.
4. Критерий пессимизма-оптимизма Гурвица (П-О)
Для каждой строки рассчитываем значение критерия по формуле:W1 = 0,4∙min{2; -3; 7} + (1-0,4) ∙ max{2; -3; 7} = 0,4∙(-3) + 0,6∙7 = -1,2 + 4,2 = 3
W2 = 0,4∙min{-1; 5; 4} + (1-0,4) ∙ max{-1; 5; 4} = 0,4∙(-1) + 0,6∙5 = -0,4 + 3 = 2,6
W3 = 0,4∙min{-7; 13; -3} + (1-0,4) ∙ max{-7; 13; -3} = 0,4∙(-7) + 0,6∙13 = -2,8 + 7,2 = 5
Найденные значения заносим в четвертый столбец (П-О) и выбираем максимальное W = max{3; 2.6 5} = 5, значит оптимальной по данному критерию является стратегия А3 – продавать в весенние месяцы.
5. Критерий Ходжа-Лемана (Х-Л)
Для каждой строки рассчитываем значение критерия по формуле:W1 = 0,6∙1 + (1-0,6) ∙(-3) = 0,6 – 1,2 = -0,6
W2 = 0,6∙3,5 + (1-0,6) ∙(-1) = 2,1 – 0,4 = 1,7
W3 = 0,6∙4,2 + (1-0,6) ∙(-7) = 2,52 – 2,8 = -0,28
Найденные значения заносим в пятый столбец (Х-Л) и выбираем максимальное W = max{-0.6; 1.7; -0.28} = 1.7, значит оптимальной по данному критерию является стратегия А2 – продавать в зимние месяцы.
5. Критерий минимаксного риска Сэвиджа
Рассчитаем матрицу рисков. Заполнять ее лучше по столбцам. В каждом столбце находим максимальный элемент и вы читаем из него все остальные элементы столбца, результаты записываем на соответствующих местах.Вот как рассчитывается первый столбец. Максимальный элемент в первом столбце: a11 = 2, значит по формуле
r11 = 2 – a11 = 2 -2 = 0
r21 = 2 – a21 = 2 –(-1) = 3
r31 = 2 – a31 = 2 –(-7) = 9
Рассчитаем второй столбец матрицы рисков. Максимальный элемент во втором столбце: a32 = 13, значит:
r12 = 13 – a12 = 13 –(-3) = 16
r22 = 13 – a22 = 13 –5 = 8
r32 = 13 – a32 = 13 –13 = 0
Рассчитаем третий столбец матрицы рисков. Максимальный элемент в третьем столбце: a13 = 7, значит:
r13 = 7 – a13 = 7 –7 = 0
r23 = 7 – a23 = 7 –4 = 3
r33 = 7 – a33 = 7 –(-3) = 10
Таким образом, матрица рисков имеет вид (в каждом столбце на месте максимального элемента платежной матрицы должен стоять ноль):
| Wi | |||
| 0 | 16 | 0 | 16 |
| 3 | 8 | 3 | 8 |
| 9 | 0 | 10 | 10 |
W1 = max{0; 16; 0} = 16
W2 = max{3; 8; 3} = 8
W3 = max{9; 0; 10} = 10
Найденные значения заносим в столбец (Wi) и выбираем минимальное W = min{16,8,10} = 8, значит оптимальной по данному критерию является стратегия А2 – продавать в зимние месяцы.
Вывод:
- Стратегия А1 (продавать сразу после уборки) не является оптимальной ни по одному из критериев.
- Стратегия А2 (продавать в зимние месяцы) является оптимальной согласно критериям недостаточного основания Лапласа, максиминного критерия Вальда и минимаксного критерия Сэвиджа.
- Стратегия А3 (продавать в весенние месяцы) является оптимальной согласно критериям Байеса, пессимизма-оптимизма Гурвица, Ходжа-Лемана.
Пример №2. В обычной стратегической игре каждый игрок предпринимает именно те действия, которые наиболее выгодны ему и менее выгодны противнику. При этом предполагается, что игроки – разумные и антагонистические противники. Однако очень часто присутствует неопределенность, которая не связана с сознательным противодействием противника, а зависит от некоторой объективной действительности.
Сельскохозяйственное предприятие имеет три участка земли: влажный, средней влажности и сухой. Один из этих участков предполагается использовать для выращивания картофеля, остальные – для посева зеленой массы. Для получения хорошего урожая картофеля требуется определенное количество влаги в почве в период вегетации. При излишней влажности посаженый картофель на некоторых участках может гнить, а при недостаточном количестве осадков будет плохо развиваться, что приводит к снижению урожайности. Определить, на каком участке сеять картофель, чтобы получить хороший урожай его, если известна средняя урожайность картофеля на каждом участке в зависимости от погодных условий. На участке A1 урожайность составляет 200, 100 и 250 ц с 1 га при выпадении соответственно нормального количества осадков, больше и меньше нормы. Аналогично на участке A2 – 230, 120 и 200 ц, а на участке A3 – 240, 260 и 100 ц.
Используем игровой подход. С/х предприятие – игрок A, у которого три стратегии: A1 – сеять картофель на влажном участке, A2 – на участке средней влажности, A3 – на сухом участке. Игрок П – природа, у которого три стратегии: П1 соответствует количеству осадков меньше нормы, П2 – норме, П3 – больше нормы. Выигрыш с/х предприятия при каждой паре стратегий (Ai, Пj) задается урожайностью картофеля с 1 га.
| П A | П1 | П2 | П3 |
| A1 | 250 | 200 | 100 |
| A2 | 200 | 230 | 120 |
| A3 | 100 | 240 | 260 |
Может показаться, что игра с природой проще стратегической игры, поскольку природа не противодействует игроку A. На самом деле это не так, поскольку в неопределенной ситуации труднее принять обоснованное решение. Хотя выиграет A, скорее всего, больше, чем в игре против сознательного противника.
Пример 9. Фирма производит пользующиеся спросом детские платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение августа-сентября на единицу продукции составили: платья – 7 ден. ед., костюмы – 28 ден. ед. Цена реализации составляет 15 и 50 ден. ед. соответственно. По данным наблюдений за несколько предыдущих лет, фирма может реализовать в условиях теплой погоды 1 950 платьев и 610 костюмов, а при прохладной погоде – 630 платьев и 1 050 костюмов.
Составить платежную матрицу.
Решение. У фирмы две стратегии: A1: выпустить продукцию, считая, что погода будет теплой; A2: выпустить продукцию, считая, что погода будет прохладной.
У природы две стратегии: B1: погода теплая; B2: погода прохладная.
Найдем элементы платежной матрицы:
1) a11 – доход фирмы при выборе стратегии A1 при условии B1:
a11=(15-7)·1950+(50-28)·610=29020.
2) a12 – доход фирмы при выборе A1 при условии B2. Фирма выпустит 1 950 платьев, а продаст 630, доход от реализации платьев
(15-7)·630-7·(1950-630)=5040-9240
a12=5040-9240+22·610=9220.
3) аналогично при стратегии A2 в условиях B1 фирма выпустит 1 050 костюмов, а продаст 610;
a21=8·630+22·610-28·(1050-610)=6140
4) a22=8·630+22·1050=28140
Платежная матрица:
| 20 020 | 9 220 |
| 6 140 | 28 140 |
Пример 2. Объединение производит разведку полезных ископаемых на трех месторождениях. Фонд средств объединения составляет 30 ден. ед. Деньги в первое месторождение M1 могут быть вложены в количестве, кратном 9 ден. ед., во второе M2 – 6 ден. ед., в третье M3 – 15 ден. ед. Цены на полезные ископаемые в конце планового периода могут оказаться в двух состояниях: C1 и C2. Эксперты установили, что в ситуации C1 прибыль от месторождения M1 составит 20 % от количества вложенных ден. ед. на разработку, на M2 – 12 % и на M3 – 15 %. В ситуации C1 на конец планового периода прибыль составит 17 %, 15 %, 23 % на месторождениях M1, M3, M3 соответственно.
Игрок A – объединение. Игрок П (природа) – совокупность внешних обстоятельств, которые обуславливают ту или иную прибыль на месторождениях. У игрока A имеется четыре возможности, полностью использующие имеющиеся средства. Первая стратегия, A1, состоит в том, что A вложит в M1 9 ден. ед., в M2 – 6 ден. ед., в M3 – 15 ден. ед. Вторая стратегия A2: в M1 – 18 ден. ед., в M2 – 12 ден. ед., в M3 деньги не вкладывать. Третья стратегия, A3: 30 ден. ед. вложить в M3. Четвертая стратегия, A4:. 30 ден. ед. вложить в M2. Кратко можно записать A1 (9, 6, 15), A2 (18, 12, 0), A3 (0, 0, 30), A4 (0, 30, 0).
Природа может реализовать одно из двух своих состояний, характеризующихся различными ценами на полезные ископаемые в конце планового периода. Обозначим состояния природы П1 (20 %, 12 %, 15 %), П2 (17 %, 15 %, 23 %).
Элементы aij платежной матрицы имеют смысл суммарной прибыли, получаемой объединением в различных ситуациях (Ai, Пj) (i=1, 2, 3, 4, j = 1, 2). Например, вычислим a12, отвечающий ситуации (A1, П2), т. е. случаю, когда объединение вкладывает в месторождения M1, M2, M3, соответственно 9 ден. ед., 6 ден. ед., 15 ден. ед., и на конец планового периода цены оказались в состоянии C2:
a12 = 9·0,17+6·0,15+15·0,23 = 5,88 ден. ед.
Пример 3. Ожидается наступление наводнения, которое может иметь категорию с первой по пятую. Величина ущерба от наводнения:
| Категория наводнения | 1 | 2 | 3 | 4 | 5 |
| Ущерб, ден. ед. | 5 | 10 | 13 | 16 | 20 |
Затраты на строительство дамбы:
| Высота дамбы | h1 | h2 | h3 | h4 | h5 |
| Затраты, ден. ед. | 2 | 4 | 6 | 8 | 10 |
Получаем матрицу потерь:
| П / A | П0 | П1 | П2 | П3 | П4 | П5 |
| A0 | 0 | 5 | 10 | 13 | 16 | 20 |
| A1 | 2 | 2 | 12 | 15 | 18 | 22 |
| A2 | 4 | 4 | 4 | 17 | 20 | 24 |
| A3 | 6 | 6 | 6 | 6 | 22 | 26 |
| A4 | 8 | 8 | 8 | 8 | 8 | 28 |
| A5 | 10 | 10 | 10 | 10 | 10 | 10 |
Чтобы из матрицы потерь (bij) получить матрицу выигрышей, достаточно у всех элементов поменять знак и прибавить любую константу C (в данном случае C можно интерпретировать как сумму, выделенную на строительство дамбы, тогда выигрыш aij=C-bij представляет собой сэкономленную сумму). Например, при C=30 матрица выигрышей:
| П / A | П0 | П1 | П2 | П3 | П4 | П5 |
| A0 | 30 | 25 | 20 | 17 | 14 | 10 |
| A1 | 28 | 28 | 18 | 15 | 12 | 8 |
| A2 | 26 | 26 | 26 | 13 | 10 | 6 |
| A3 | 24 | 24 | 24 | 24 | 8 | 4 |
| A4 | 22 | 22 | 22 | 22 | 22 | 2 |
| A5 | 20 | 20 | 20 | 20 | 20 | 20 |
Игры с "природой"
Термин "природа" в теории игр понимается в широком смысле. Это могут быть действительные природные физические (климатические), биологические, химические, социальные и т.п. процессы, которые сопровождают экономическую деятельность. Под "природой" может также пониматься рынок, противостоящий предпринимателю, конкурирующая среда, монополия и т.п. "Природа" может выступать как антагонистическая сторона, а может как кооперативная среда. "Природа" в виде природных процессов, как часть экономики, не стремиться "специально" навредить предпринимателю, но она несёт определённый урон от его экономической деятельности и этот "проигрыш"для неё должен быть минимален, если, вообще, без него для окружающей среды нельзя обойтись. Игрок A в таких играх - это экономические субъекты, а игрок B - это "природа". Откуда средства у физической "природы"? Проигрыш игрока B, физической "природы", должен компенсироваться из вне, например, государственными дотациями либо заложенными в инвестиционные проекты средствами на возобновление природных ресурсов. Знание оптимальных стратегий "природы" позволяет определить наиболее неблагоприятные условия для игрока A (предпринимателя), которые его ожидают ("надейся на лучшее, но готовься к худшему"), и оценить необходимые ресурсы на восстановление природных ресурсов, дающих ему возможность получить гарантированный доход.Если "природа" подразумевает конкурентную среду - то проигрыш второго игрока есть цена борьбы с конкурентами на рынке.
Перейдём к примерам содержательных постановок задач игры с "природой".
1. Антагонистические игры
Пример 1. (Планирование посевов). Фермер, имеющий ограниченный участок земельных угодий, может его засадить тремя различными культурами A1, A2, A3. Урожай этих культур зависит главным образом от погоды ("природы"), которая может находиться в трёх различных состояниях: B1, B2, B3. Фермер имеет информацию (статистические данные) о средней урожайности этих культур (количество центнеров культуры, получаемого в одного гектара земли) при трёх различных состояниях погоды, которая отражена в таблице:
| Виды культур | Возможные состояния погоды | Цены | ||
| Засуха B1 | Нормальная B2 | Дождливая B3 | ||
| A1 | 20 | 15 | 10 | 5 |
| A2 | 7 | 15 | 5 | 7 |
| A3 | 0 | 5 | 10 | 10 |
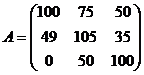
Элемент матрицы A - (aij) показывает, какой доход может получить фермер с одного гектара земли, если он посеет культуру i (i =1, 2, 3), а погода будет находиться в состоянии j (j = 1, 2, 3).
Необходимо определить пропорции, в которых фермер должен засеять имеющийся участок земли, чтобы получить максимальный гарантированный доход вне зависимости от того, какие погодные условия будут реализованы.
Данная задача может быть сведена к антагонистической игре. В данном случае в качестве первого игрока выступает фермер, а в качестве второго игрока - природа. Будем предполагать, что природа, как игрок, может вести себя таким образом, чтобы максимально навредить фермеру, преследуя тем самым противоположные интересы (эти предположения позволяют оценить тот доход, который он может получить в том случае, если погодные условия будут для него максимально неблагоприятные). В этом случае фермер имеет в своём распоряжении три чистые стратегии:
- первая чистая стратегия предполагает, что весь участок земли буде засеян культурой A1;
- вторая чистая стратегия предполагает, что весь участок земли будет засеян культурой A2;
- третья чистая стратегия предполагает, что весь участок будет засеян культурой A3.
- засушливую погоду, которая соответствует первой чистой стратегии B1;
- нормальную погоду, которая соответствует второй чистой стратегии B2;
- дождливую погоду, которая соответствует третьей чистой стратегии B3.
1. Проанализируем платёжную матрицу A.
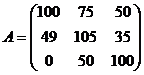
Матрица A не имеет доминируемых стратегий и не может быть упрощена.
2. Проверим, имеет ли данная игра седловую точку.
Найдём нижнюю и верхнюю цену игры:
V*=maxi minjaij = 50.
V*=minjmaxiaij = 100.
Поскольку V* ≠V*, то данная антагонистическая игра не имеет седловой точки и решения в чистых стратегиях.
3. Решение игры следует искать в смешанных стратегиях. Сведём игровую задачу к задаче линейного программирования. Если первый игрок - фермер - применяет свою оптимальную смешанную стратегию P*, а второй игрок - природа - применяет последовательно свои чистые стратегии, то математическое ожидание дохода, который фермер может получить со своего участка, будет не меньше цены игры V. Следовательно, должна выполняться следующая система неравенств:
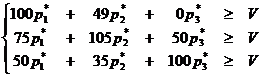
Разделим каждое из неравенств, входящих в систему на V и введём новые переменные:
В результате получим новую систему неравенств:
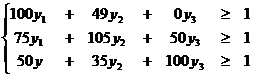
Разделим равенство:
p*1 + p*2 + p*3 = 1
на V, получим, что новые переменные y1, y2, y3 удовлетворяют условию:
y1 + y2 + y3 = 1/V
Поскольку цель первого игрока - максимизация его выигрыша, а математическое ожидание его выигрыша не меньше цены игры, то первый игрок будет стремиться максимизировать цену игры, которая эквивалентна минимизации величины 1/V.
Итак, для первого игрока (фермера) задача об определении оптимальной стратегии поведения свелась к задаче линейного программирования:
найти минимум функции F = y1 + y2 + y3
при следующих функциональных ограничениях:
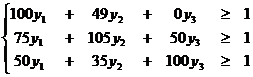
и прямых ограничениях:
y1 ≥ 0, y2≥ 0, y3≥ 0
Переходим ко второму игроку, к природе. Если второй игрок - природа - будет применять свою оптимальную смешанную стратегию Q*,а первый игрок - фермер будет последовательно применять свои чистые стратегии, то математическое ожидание проигрыша второго игрока будет не больше цены игры. Следовательно, должна выполняться следующая система неравенств:
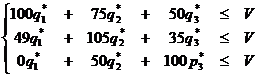
Разделим каждое из неравенств, входящих в систему на V и введём новые переменные:
В результате получим новую систему неравенств:
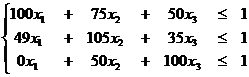
Разделим равенство:
q*1 + q*2 + q*3 = 1
на V, получим, что новые переменные q1 , q2 , q3 удовлетворяют условию:
q1 + q2 + q3 = 1/V
Поскольку цель второго игрока - природы - минимизация его проигрыша, а математическое ожидание его проигрыша не больше цены игры, то второй игрок будет стремиться минимизировать цену игры, которая эквивалентна максимизации величины 1/V.
Итак, для второго игрока (природы) задача об определении оптимальной стратегии поведения свелась к задаче линейного программирования:
найти максимум функции F/ = x1 + x2 + x3
при следующих функциональных ограничениях:
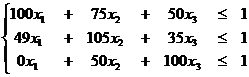
и прямых ограничениях:
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0
Таким образом, для того чтобы найти оптимальную смешенную стратегию второго игрока, необходимо также решить задачу линейного программирования.
Задачи обоих игроков свелись к паре двойственных задач линейного программирования:
| Задача второго игрока минимизация проигрыша V | Задача первого игрока максимизация выигрыша V |
| Целевая функция | |
F/= x1+x2+x3= 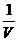  → max → max | F = y1+y2+y3 = 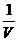 → min → min |
| Функциональные ограничения | |
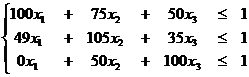 | 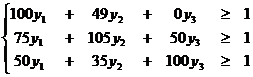 |
| Прямые ограничения | |
x1≥ 0, x2≥ 0, x3≥ 0 | y1≥ 0, y2≥ 0, y3≥ 0 |
Задача первого игрока решается симплекс-методом. Результаты счёта:
| у1 = | 0,01 | p1 = | 0,67 |
| у2 = | 0 | p2 = | 0,00 |
| у3 = | 0,005 | p3 = | 0,33 |
| F = | 0,015 | V = | 66,67 |
Задача второго игрока решается также симплекс-методом. Результаты счёта:
| x1 = | 0,005 | p1 = | 0,33 |
| x2 = | 0 | p2 = | 0,00 |
| x3 = | 0,01 | p3 = | 0,67 |
| F = | 0,015 | V = | 66,67 |
Выводы. В соответствии с полученными результатами фермеру гарантирован средний доход в размере 66,67 единицс каждого гектара используемой под культурами земли при самых неблагоприятных условиях. Оптимальная стратегия для него - выращивание двух культур, A1и A3, причём, под первую культуруему следует отвести 0,67 часть всей земли, а под третью культуру 0,33 часть всей земли.
Природа "грозит" фермеру жарой 0,33 часть сезона возделывания культур и 0,67 часть сезона дождями.
Пример. Планирование выпуска продукции при разных состояниях природы - рынка спроса.
Предприятие может выпускать 4 вида продукции: A1, A2, A3, A4, получая при этом прибыль. Её величина определяется состоянием спроса (природой рынка), который может находиться в одном из четырёх возможных состояний: B1, B2, B3, B4. Зависимость величины прибыли от вида продукции и состояния рынка представлено в таблице:
| Виды продукции | Возможные состояния рынка спроса | |||
| B1 | B2 | B3 | B4 | |
| A1 | 4 | 3 | 5 | 6 |
| A2 | 2 | 6 | 1 | 5 |
| A3 | 3 | 0 | 7 | 2 |
| A4 | 3 | 5 | 1 | 3 |
Платёжная матрица имеет вид:
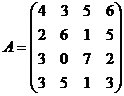
Элемент матрицы A - {aij} характеризует, какую прибыль может получить предприятие, если оно будет выпускать i- й вид продукции(i =1, 2, 3, 4) при j-м спросе(j = 1, 2, 3, 4).
Необходимо определить оптимальные пропорции выпускаемых предприятием видов продукции, продажа которой обеспечила бы ему максимально возможную выручку вне зависимости от того, какое состояние спроса будет реализовано
Эта задача может быть сведена к антагонистической игре.
В данном случае в качестве первого игрока выступает предприятие, а в качестве второго игрока - природа, которая влияет на состояние спроса и может сделать его максимально неблагоприятным для предприятия. Будем предполагать, что природа, как игрок, будет вести себя таким образом, чтобы максимально навредить предприятию, преследуя тем самым противоположные интересы.
В этом случае конфликт двух сторон может характеризоваться, как антагонистический, а использование модели этого конфликта позволяет предприятию. оценить выручку, которую оно может получить вне зависимости от того, какое состояние спроса будет реализовано.
Выступая в качестве первого игрока, предприятие может использовать четыре стратегии:
· первую чистую стратегию, соответствующую выпуску предприятием только продукции A1
· вторую чистую стратегию, соответствующую выпуску предприятием только продукции A2
· третью чистую стратегию, соответствующую выпуску предприятием только продукции A3
· четвёртую чистую стратегию, соответствующую выпуску предприятием только продукции A4
Выступая в качестве второго игрока, природа может использовать также четыре стратегии:
· первую чистую стратегию, при которой реализуется состояние спроса B1;
· вторую чистую стратегию, при которой реализуется состояние спроса B2;
· третью чистую стратегию, при которой реализуется состояние спроса B3;
· четвёртую чистую стратегию, при которой реализуется состояние спроса B4.
Решение
1. Проанализируем платёжную матрицу A.
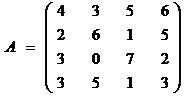
Матрица A не имеет доминируемых стратегий и не может быть упрощена.
2. Проверим, имеет ли данная игра седловую точку.
Найдём нижнюю и верхнюю цену игры:
V*=maxi minj aij = 3.
V*=minj maxiaij = 4.
Поскольку V* ≠V*, то данная антагонистическая игра не имеет седловой точки и решения в чистых стратегиях.
Решение игры следует искать в смешанных стратегиях. Сведём рассматриваемый антагонистический конфликт к прямой и двойственной задаче линейного программирования.
Если первый игрок - предприятие - применяет свою оптимальную смешанную стратегию P*, а второй игрок - природа - применяет последовательно свои чистые стратегии, то математическое ожидание дохода, который предприятие может получить, будет не меньше цены игры V.
И наоборот, если второй игрок - природа - будет применять свою оптимальную смешанную стратегию Q*,а первый игрок - предприятие будет последовательно применять свои чистые стратегии, то математическое ожидание проигрыша второго игрока будет не больше цены игры. Следовательно, должна выполняться следующая система неравенств:
| Задача второго игрока минимизация проигрыша V | Задача первого игрока максимизация выигрыша V |
| Целевая функция | |
|
F/ = x1+x2+x3+x4 = |
F = y1+y2+y3+y4
= |
| Функциональные ограничения | |
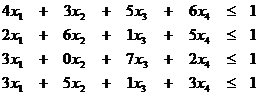 |
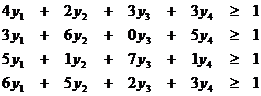 |
| Прямые ограничения | |
|
x1 ≥ 0, x2 ≥ 0, x3 ≥ 0, x4 ≥ 0 |
y1 ≥ 0, y2 ≥ 0, y3 ≥ 0, y4 ≥ 0 |
Y*= (y1* = 0,182; y2* = 0; y3* = 0; y4* =0,091)
F= y1*+ y2*+ y3*+y4*= 0,273
Из соотношения y1*+ y2*+ y3*+y4*=1/V найдём V:
Из соотношений:
Найдём:
p*1 = y*1V = 0,67 , p*2 = y*2V = 0 , p*3 = y*3V = 0 , p*4 = y*4V =0,33
Окончательно имеем:
Р*= (р*1 =0,67; р*2= 0; р*3=0; р*4 = 0,33), V = 3.67
На основании решения, найденного для двойственной задачи линейного программирования, найдём решение исходной задачи - задачи второго игрока:
X*= (x1* = 0,121; x2* =0,121; x3* = 0,03; x4* = 0)
F/ = x1*+ x2*+ x3*+x4*= 0,273
Из соотношения x1*+ x2*+ x3*+x4* = 1/V найдём V:
Из соотношений:
Найдём:
q*1 = x*1V = 0,445 , q*2 = x*2V = 0,444 , q*3 = x*3V = 0,111 , q*4 = x*4V = 0.
Окончательно имеем:
Q*= (q*1= 0,445; q*2=0,444; q*3= 0,111; q*4= 0), V = 3.67
Пример. Фирма планирует реализацию своей продукции на рынках, учитывая возможные варианты покупательского спроса Пj, j=1,4 (низкий, средний, высокий, очень высокий). На предприятии разработано три стратегии сбыта товаров A1, А2, А3. Объем товарооборота (ден.ед.), зависящий от стратегии и покупательского спроса, представлен в таблице.
| Аj | Пj | |||
| П1 | П2 | П3 | П4 | |
| А1 | 30 +N | 10 | 20 | 25 + N/2 |
| А2 | 50 | 70 - N | 10 + N/2 | 25 |
| А3 | 25 – N/2 | 35 | 40 | 60 - N/2 |
Известны возможные состояния покупательского спроса, которые соответственно q1=0,3, q2=0,2, q3=0,4, q4=0,1. Необходимо найти стратегию сбыта, максимизирующую средний товарооборот фирмы. При этом использовать критерии Вальда, Гурвица, Сэвиджа, Байеса.
Решение находим с помощью калькулятора.
Критерий Байеса.
По критерию Байеса за оптимальные принимается та стратегия (чистая) Ai, при которой максимизируется средний выигрыш a или минимизируется средний риск r.
Считаем значения ∑(aijpj)
∑(a1,jpj) = 33•0.3 + 10•0.2 + 20•0.4 + 26.5•0.1 = 22.55
∑(a2,jpj) = 50•0.3 + 67•0.2 + 11.5•0.4 + 25•0.1 = 35.5
∑(a3,jpj) = 23.5•0.3 + 35•0.2 + 40•0.4 + 58.5•0.1 = 35.9
| Ai | П1 | П2 | П3 | П4 | ∑(aijpj) |
| A1 | 9.9 | 2 | 8 | 2.65 | 22.55 |
| A2 | 15 | 13.4 | 4.6 | 2.5 | 35.5 |
| A3 | 7.05 | 7 | 16 | 5.85 | 35.9 |
| pj | 0.3 | 0.2 | 0.4 | 0.1 |
Критерий Лапласа.
Если вероятности состояний природы правдоподобны, для их оценки используют принцип недостаточного основания Лапласа, согласно которого все состояния природы полагаются равновероятными, т.е.:
q1 = q2 = ... = qn = 1/n.
qi = 1/4
| Ai | П1 | П2 | П3 | П4 | ∑(aij) |
| A1 | 8.25 | 2.5 | 5 | 6.63 | 22.38 |
| A2 | 12.5 | 16.75 | 2.88 | 6.25 | 38.38 |
| A3 | 5.88 | 8.75 | 10 | 14.63 | 39.25 |
| pj | 0.25 | 0.25 | 0.25 | 0.25 |
Критерий Вальда.
По критерию Вальда за оптимальную принимается чистая стратегия, которая в наихудших условиях гарантирует максимальный выигрыш, т.е.
a = max(min aij)
Критерий Вальда ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
| Ai | П1 | П2 | П3 | П4 | min(aij) |
| A1 | 33 | 10 | 20 | 26.5 | 10 |
| A2 | 50 | 67 | 11.5 | 25 | 11.5 |
| A3 | 23.5 | 35 | 40 | 58.5 | 23.5 |
Критерий Севиджа.
Критерий минимального риска Севиджа рекомендует выбирать в качестве оптимальной стратегии ту, при которой величина максимального риска минимизируется в наихудших условиях, т.е. обеспечивается:
a = min(max rij)
Критерий Сэвиджа ориентирует статистику на самые неблагоприятные состояния природы, т.е. этот критерий выражает пессимистическую оценку ситуации.
Находим матрицу рисков.
Риск – мера несоответствия между разными возможными результатами принятия определенных стратегий. Максимальный выигрыш в j-м столбце bj = max(aij) характеризует благоприятность состояния природы.
1. Рассчитываем 1-й столбец матрицы рисков.
r11 = 50 - 33 = 17; r21 = 50 - 50 = 0; r31 = 50 - 23.5 = 26.5;
2. Рассчитываем 2-й столбец матрицы рисков.
r12 = 67 - 10 = 57; r22 = 67 - 67 = 0; r32 = 67 - 35 = 32;
3. Рассчитываем 3-й столбец матрицы рисков.
r13 = 40 - 20 = 20; r23 = 40 - 11.5 = 28.5; r33 = 40 - 40 = 0;
4. Рассчитываем 4-й столбец матрицы рисков.
r14 = 58.5 - 26.5 = 32; r24 = 58.5 - 25 = 33.5; r34 = 58.5 - 58.5 = 0;
| Ai | П1 | П2 | П3 | П4 |
| A1 | 17 | 57 | 20 | 32 |
| A2 | 0 | 0 | 28.5 | 33.5 |
| A3 | 26.5 | 32 | 0 | 0 |
| Ai | П1 | П2 | П3 | П4 | max(aij) |
| A1 | 17 | 57 | 20 | 32 | 57 |
| A2 | 0 | 0 | 28.5 | 33.5 | 33.5 |
| A3 | 26.5 | 32 | 0 | 0 | 32 |
Критерий Гурвица.
Критерий Гурвица является критерием пессимизма - оптимизма. За (оптимальную принимается та стратегия, для которой выполняется соотношение:
max(si)
где si = y min(aij) + (1-y)max(aij)
При y = 1 получим критерий Вальде, при y = 0 получим – оптимистический критерий (максимакс).
Критерий Гурвица учитывает возможность как наихудшего, так и наилучшего для человека поведения природы. Как выбирается y? Чем хуже последствия ошибочных решений, тем больше желание застраховаться от ошибок, тем y ближе к 1.
Рассчитываем si.
s1 = 0.5•10+(1-0.5)•33 = 21.5
s2 = 0.5•11.5+(1-0.5)•67 = 39.25
s3 = 0.5•23.5+(1-0.5)•58.5 = 41
| Ai | П1 | П2 | П3 | П4 | min(aij) | max(aij) | y min(aij) + (1-y)max(aij) |
| A1 | 33 | 10 | 20 | 26.5 | 10 | 33 | 21.5 |
| A2 | 50 | 67 | 11.5 | 25 | 11.5 | 67 | 39.25 |
| A3 | 23.5 | 35 | 40 | 58.5 | 23.5 | 58.5 | 41 |
Таким образом, в результате решения статистической игры по различным критериям чаще других рекомендовалась стратегия A3.
Руководство компании принимает решение о размещении производства нового продукта в некотором месте. Чтобы сформировать представление о ситуации на рынке нового продукта на момент освоения производства, ему необходимо учесть затраты на доставку готовой продукции до потребителя, развитость транспортной и социальной инфраструктуры региона, конкуренцию на рынке, соотношение спроса и предложения, курсы валют и многое другое. Возможные варианты решений, инвестиционная привлекательность которых определяется как процент прироста дохода по отношению к сумме капитальных вложений, представлены в таблице.
Выбрать:
1) место для размещения производства, если руководитель предприятия уверен в том, что на рынке сложится ситуация 4;
2) место для размещения производства, если руководство оценивает вероятность ситуации 1 в 0,2; ситуации 2 в 0,1; ситуации 3 в 0,25;
3) провести выбор варианта в условиях неопределенности по критерию: максимакс, максимин, критерий Лапласа, критерий Сэведжа, критерий Гурвица (y = 0,3);
4) изменится ли наилучший вариант решения по критерию Гурвица если величину a увеличить до 0,5?
5) предположив, что данные таблицы представляют затраты предприятия, определить выбор, который сделает предприятие при использовании каждого из следующих критериев: максимин; максимакс; критерий Гурвица(? = 0,3); критерий Сэведжа; критерий Лапласа
Типовые задания
- Выбрать оптимальный проект для строительства используя критерии Лапласа, Вальда, максимального оптимизма, Сэвиджа и Гурвица при a=0.58. Матрица затрат имеет вид:
0.07 0.26 0.11 0.25 0.1 0.21 68 45 54 79 47 99 56 89 42 56 74 81 72 87 56 40 62 42 65 48 75 89 52 80 69 93 93 56 45 43 73 94 79 68 67 46 66 100 64 89 94 49 70 42 97 42 42 50 - Розничное торговое, предприятие разработало несколько вариантов плана продажи товаров на предстоящей ярмарке с учетом меняющейся конъюнктуры рынка и спроса покупателей, получающиеся от их возможных сочетаний величины прибыли представлены в виде матрицы выигрышей. Определить оптимальный план продажи товаров.
x=0,7Величина прибыли, тыс. руб. План продажи Состояние конъюнктуры рынка E1 E2 E3 E4 I1 5,0 4,5 5,1 4,0 I2 4,2 5,6 3,9 4,3 I3 3,6 4,1 4,7 4,0 I4 3,5 3,9 4,6 3,8 - Фирма планирует реализацию своей продукции на рынках, учитывая возможные варианты покупательского спроса Пj, j=1͞,4͞ (низкий, средний, высокий, очень высокий). На предприятии разработано три стратегии сбыта товаров A1, А2, А3. Объем товарооборота (ден.ед.), зависящий от стратегии и покупательского спроса, представлен в таблице.
Аj Пj П1 П2 П3 П4 А1 30 +N 10 20 25 + N/2 А2 50 70 - N 10 + N/2 25 А3 25 – N/2 35 40 60 - N
Где N=3
Известны возможные состояния покупательского спроса, которые соответственно q1=0,3, q2=0,2, q3=0,4, q4=0,1. Необходимо найти стратегию сбыта, максимизирующую средний товарооборот фирмы. При этом использовать критерии Вальда, Гурвица, Сэвиджа, Байеса.
Решение - Затраты фабрики в течение апреля — мая на единицу продукции составили: платья — 8 денежных единиц, костюмы — 27, а цена реализации равняется соответственно 16 и 48. По данным наблюдений за прошлое время, фабрика может реализовать в течение этих месяцев в условиях теплой погоды 600 костюмов и 1975 платьев, а при прохладной погоде — 625 платьев и 1000 костюмов.
Решение