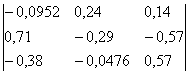Нахождение обратной матрицы методом Жордано-Гаусса
Назначение сервиса. С помощью онлайн-калькулятора вычисляется обратная матрица посредством алгоритма Жордано-Гаусса. Обратную матрицу также можно вычислить посредством нахождения алгебраических дополнений (перейти). Результаты вычислений оформляются в отчете формата Word. Для проверки вычислений создается шаблон решения в формате Excel.Возьмём две матрицы: саму A и единичную E. Приведём матрицу A к единичной матрице методом Гаусса—Жордана.
После применения каждой операции к первой матрице применим ту же операцию ко второй. Когда приведение первой матрицы к единичному виду будет завершено, вторая матрица окажется равной A-1.
Запишем систему в виде:
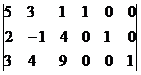
Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен 5.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
НЭ = СЭ - (А*В)/РЭ
РЭ - разрешающий элемент (5), А и В - элементы матрицы, образующие прямоугольник с элементами СТЭ и РЭ.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | x4 | x5 | x6 |
| 5 / 5 = 1 | 3 / 5 = 0.6 | 1 / 5 = 0.2 | 1 / 5 = 0.2 | 0 / 5 = 0 | 0 / 5 = 0 |
Представим расчет каждого элемента в виде таблицы:
Посмотреть таблицу
Обратная матрица A-1:
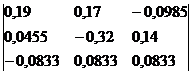
Пример №2.
Запишем систему в виде:

Последовательно будем выбирать разрешающий элемент РЭ, который лежит на главной диагонали матрицы.
Разрешающий элемент равен 4.
На месте разрешающего элемента получаем 1, а в самом столбце записываем нули.
Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника.
Представим расчет каждого элемента в виде таблицы:
| x1 | x2 | x3 | x4 | x5 | x6 |
| 4 / 4 = 1 | 3 / 4 = 0.75 | 2 / 4 = 0.5 | 1 / 4 = 0.25 | 0 / 4 = 0 | 0 / 4 = 0 |
| | | | | | |
| |
| |
| |
|
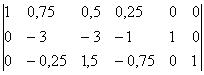
Разрешающий элемент равен -3. На месте разрешающего элемента получаем 1, а в самом столбце записываем нули. Все остальные элементы матрицы, включая элементы столбца B, определяются по правилу прямоугольника. Для этого выбираем четыре числа, которые расположены в вершинах прямоугольника и всегда включают разрешающий элемент РЭ.
Представим расчет каждого элемента в виде таблицы:
Посмотреть таблицу
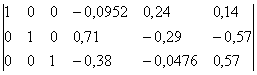
Обратная матрица A-1: