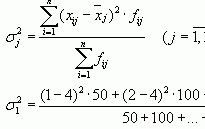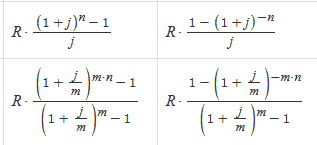Децили
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9.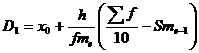
, 
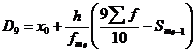
По заданному вариационному ряду найдем децили с помощью калькулятора.
| Группы | x | Кол-во f | x·f | S | (x-x)·f | (x-x)2·f | (x-x)3·f | (x-x)4·f | Частота |
| 0.06 - 0.27 | 0.16 | 2 | 0.33 | 2 | 0.72 | 0.26 | -0.0926 | 0.0333 | 0.1 |
| 0.27 - 0.47 | 0.37 | 7 | 2.59 | 9 | 1.08 | 0.17 | -0.0255 | 0.0039 | 0.35 |
| 0.47 - 0.68 | 0.58 | 7 | 4.03 | 16 | 0.36 | 0.0184 | 0.0009 | 0 | 0.35 |
| 0.68 - 0.88 | 0.78 | 3 | 2.34 | 19 | 0.77 | 0.2 | 0.0506 | 0.013 | 0.15 |
| 0.88 - 1.09 | 0.99 | 0 | 0 | 19 | 0 | 0 | 0 | 0 | 0 |
| 1.09 - 1.29 | 1.19 | 1 | 1.19 | 20 | 0.67 | 0.44 | 0.3 | 0.2 | 0.05 |
| 20 | 10.47 | 0 | 3.59 | 1.08 | 0.23 | 0.25 | 1 |
Показатели центра распределения.
Средняя взвешенная
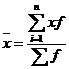
Мода
Выбираем в качестве начала интервала 0.2672, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 0.47
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
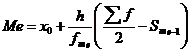
Таким образом, 50% единиц совокупности будут меньше по величине 0.5
Квартили
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1 и Q2; 25% - между Q2 и Q3; остальные 25% превосходят Q3
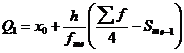
Таким образом, 25% единиц совокупности будут меньше по величине 0.36
Q2 совпадает с медианой, Q2 = 0.5
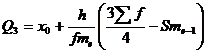
Остальные 25% превосходят значение 0.65.
Квартильный коэффициент дифференциации.
k = Q1 / Q3
k = 0.36 / 0.65 = 0.55
Расчет децили
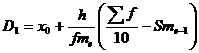
Таким образом, 10% единиц совокупности будут меньше по величине 0.27
Остальные 10% превосходят 0.81
Показатели вариации.
Размах вариации
R = Xmax - Xmin
R = 1.29 - 0.062 = 1.23
Среднее линейное отклонение
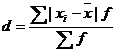
Каждое значение ряда отличается от другого не более, чем на 0.18
Дисперсия
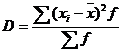
Несмещенная оценка дисперсии.
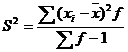
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 0.52 не более, чем на 0.23
Оценка среднеквадратического отклонения.
Коэффициент вариации
Поскольку v>30% ,но v<70%, то вариация умеренная.
Показатели формы распределения.
Коэффициент осцилляции
Относительное линейное отклонение
Относительный показатель квартильной вариации
Степень асимметрии
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Положительная величина указывает на наличие правосторонней асимметрии
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Ex > 0 - островершинное распределение
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего
Поскольку n<=30, то определяем значение tkp по таблице распределения Стьюдента
По таблице Стьюдента находим Tтабл
Ф(tkp) = 1- p = 1- 0.954 = 0.05
Tтабл (n-1;α) = (19;0.05) = 1.729
(0.52 - 0.09;0.52 + 0.09) = (0.43;0.61)
С вероятностью 0.954 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
