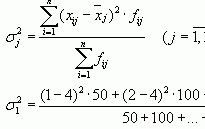Виды дисперсий
Наряду с изучением вариации признака по всей по всей совокупности в целом часто бывает необходимо проследить количественные изменения признака по группам, на которые разделяется совокупность, а также и между группами. Такое изучение вариации достигается посредством вычисления и анализа различных видов дисперсии.Выделяют дисперсию общую, межгрупповую и внутригрупповую.
Общая дисперсия σ2 измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию,
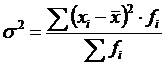 .
.
Межгрупповая дисперсия (δ) характеризует систематическую вариацию, т.е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки. Она рассчитывается по формуле:
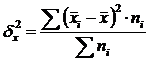 .
.
Внутригрупповая дисперсия (σ) отражает случайную вариацию, т.е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. Она вычисляется по формуле:
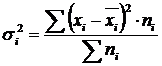 .
.
Средняя из внутригрупповых дисперсий: 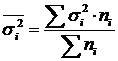 .
.
σ=σ²i+δ²i.
Данное соотношение называют правилом сложения дисперсий.
В анализе широко используется показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии. Он носит название эмпирического коэффициента детерминации (η2): 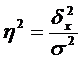 .
.
Корень квадратный из эмпирического коэффициента детерминации носит название эмпирического корреляционного отношения (η):
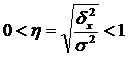 .
.
Оно характеризует влияние признака, положенного в основание группировки, на вариацию результативного признака. Эмпирическое корреляционное отношение изменяется в пределах от 0 до 1.
Покажем его практическое использование на следующем примере (табл. 1).
Пример №1. Таблица 1 - Производительность труда двух групп рабочих одного из цехов НПО «Циклон»
| Производительность труда рабочих | |||||||||
| прошедших техническое обучение
(деталей за смену) | не прошедших техническое обучение (деталей за смену) | ||||||||
| 84 | 93 | 95 | 101 | 102 | 62 | 68 | 82 | 88 | 105 |
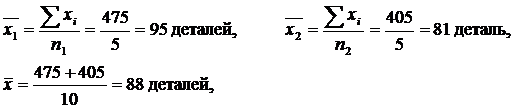
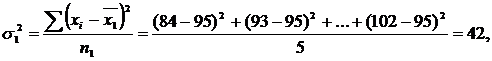
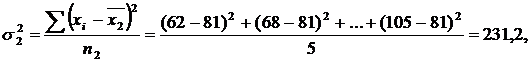
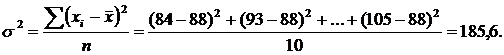
Исходные данные для вычисления средней из внутригрупповых и межгрупповой дисперсии представлены в табл. 2.
Таблица 2
Расчет и δ2 по двум группам рабочих.
|
Группы рабочих | Численность рабочих, чел. | Средняя, дет./смен. | Дисперсия |
| Прошедшие техническое обучение | 5 | 95 | 42,0 |
| Не прошедшие техническое обучение | 5 | 81 | 231,2 |
| Все рабочие | 10 | 88 | 185,6 |
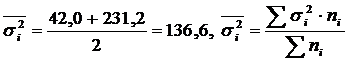
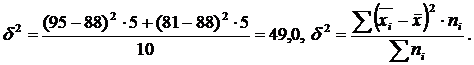
Таким образом, эмпирическое корреляционное соотношение: .
Наряду с вариацией количественных признаков может наблюдаться и вариация качественных признаков. Такое изучение вариации достигается посредством вычисления следующих видов дисперсий:
Внутригрупповая дисперсия доли определяется по формуле:
σ²pi=pi(1-pi) (1)
Средняя из внутригрупповых дисперсий рассчитывается так:
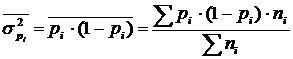 (2)
(2)
Формула межгрупповой дисперсии имеет вид:
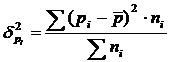 , (3)
, (3)
где ni – численность единиц в отдельных группах.
Доля изучаемого признака во всей совокупности, которая определяется по формуле:
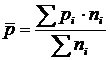 (4)
(4)
Три вида дисперсии связаны между собой следующим образом:
σ²p=σ²pi+δpi²
Это соотношение дисперсий называется теоремой сложения дисперсий доли признака.
Пример №2. Имеются следующие данные об удельном весе основных рабочих в трех цехах фирмы (табл. 2).
Таблица 2 - Удельный вес основных рабочих фирмы
| Цех | Удельный вес основных рабочих, в %, pi | Численность всех рабочих, человек, ni |
| 1 | 80 | 100 |
| 2 | 75 | 200 |
| 3 | 90 | 150 |
| Итого | — | 450 |
2) Общая дисперсия доли основных рабочих по всей фирме в целом будет равна σ2p=0.81·(1-0.81)=0.154.
3) Внутрицеховые дисперсии рассчитаем, применив формулу (1): σ²p1=0.8·0.2=0.16; σ²p2=0.75·0.25=0.19; σ²p3=0.9·0.1=0.09.
4) Средняя из внутригрупповых дисперсий будет равна (формула 5.2):
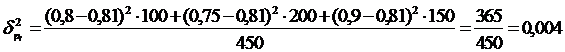
5) Межгрупповую дисперсию определим по формуле (5.3):
Проверка вычислений показывает: 0,154 = 0,15 + 0,004.
Дисперсионный анализ
| Регионы | Затраты на удобрения, тыс. руб. | Урожайность картофеля, ц/га |
| Республика Коми | 50 | 96 |
| Ленинградская область | 75 | 92 |
| Республика Хакасия | 25 | 102 |
| Архангельская область | 95 | 115 |
| Сахалинская область | 60 | 90 |
| Удмуртская республика | 70 | 92 |
| Камчатская область | 85 | 95 |
| Кировская область | 170 | 108 |
| Курганская область | 120 | 95 |
| Чувашская республика. | 160 | 99 |
| Тамбовская область | 50 | 97 |
| Республика Бурятия | 80 | 102 |
| Брянская область | 20 | 95 |
| Республика Алтай | 55 | 90 |
| Республика Адыгея | 70 | 101 |
| Республика Марий- Эл | 80 | 104 |
| Ивановская область | 100 | 120 |
| Республика Мордовия | 60 | 101 |
| Республика Северная Осетия | 50 | 95 |
| Республика Дагестан | 70 | 98 |
| Еврейская автономная область | 160 | 108 |
| Итого | 1705 | 2095 |
Среднее значение
Групповая дисперсия
Внутригрупповая дисперсия
Общая дисперсия
Межгрупповая дисперсия
Свойства дисперсии
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных): ,
,
 ,
,
среднее квадратическое отклонение (σ):
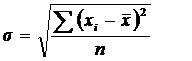 (простое среднеквадратическое отклонение),
(простое среднеквадратическое отклонение),
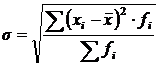 (взвешенное среднеквадратическое отклонение).
(взвешенное среднеквадратическое отклонение).
Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах, что и признак.
Расчет дисперсии может быть упрощен. В случае равных интервалов в вариационном ряду распределения используется способ отсчета от условного нуля (способ моментов). Для его понимания необходимо знать следующие свойства дисперсии:
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. Уменьшение всех значений признака на одну и ту же величину A не меняет величины дисперсии σ²(X-A)=σ²X. Значит, средний квадрат отклонений можно вычислить не по заданным значениям признака, а по отклонениям их от какого-либо постоянного числа.
Свойство 3. Уменьшение всех значений признака в K раз уменьшает дисперсию в K2 раз, а среднее квадратическое отклонение в K раз ![]() . Значит, все значения признака можно разделить на какое-то постоянное число, например, на величину интервала ряда, исчислить среднее квадратическое отклонение, а затем умножить его на постоянное число: σX=σX/K·K.
. Значит, все значения признака можно разделить на какое-то постоянное число, например, на величину интервала ряда, исчислить среднее квадратическое отклонение, а затем умножить его на постоянное число: σX=σX/K·K.
Свойство 4. Если вычислить средний квадрат отклонений от любой величины A, в той или иной степени отличающейся от средней арифметической (x), то он всегда будет больше среднего квадрата отклонений, вычисленного от средней арифметической σ²A>σ²X. Средний квадрат отклонений при этом будет больше на величину (x–A)2 :
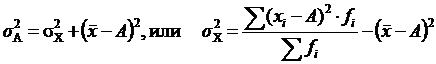
см. также свойства дисперсии для дискретной случайной величины
Рассмотрим расчет дисперсии и среднего квадратического отклонения по данным таблицы.
Таблица - Вычисление σ2 и σ по несгруппированным данным.
| Хозяйство | Валовой сбор, ц, x | xi–x | (xi–x)2 |
| А | 1 | 2 | 3 |
| 1 | 600 | 100 | 10 000 |
| 2 | 520 | 20 | 400 |
| 3 | 400 | -100 | 10 000 |
| 4 | 600 | 100 | 10 000 |
| 5 | 500 | 0 | 0 |
| 6 | 380 | -120 | 14 400 |
| ИТОГО | 3000 | 0 | 44 800 |
1) Определим среднюю величину по исходным данным (гр.1) по формуле средней арифметической простой:
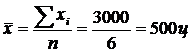 .
.
2) Находим отклонения xi от и записываем их в гр. 2. Возводим отклонения во вторую степень, отводим для них гр. 3. Их сумма – 44 800.
3) Разделив ее на число единиц совокупности, получаем дисперсию:
![]() .
.
4) Извлекая корень из второй степени получаем среднее квадратичное отклонение равное 86,4099.
Степень вариации в данной совокупности не велика, т.к. средняя величина равна 500 ц. Это говорит об однородности рассматриваемой нами совокупности.
Рассмотрим вычисление дисперсии и среднеквадратического отклонения по сгруппированным данным табл. 5.3.
Таблица 5.3 - Расчет σ2 и σ в двух вариационных рядах с разным распределением частот.
| НПО “Платан” | НПО “Исток” | ||||||||
| тариф, разряд xi | число работников, fi | xi–x | (xi–x)2 | (xi–x)2fi | тариф, разряд xi | число работников, fi | xi–x | (xi–x)2 | (xi–x)2fi |
| 12 | 1 | -3 | 9 | 9 | 12 | 30 | -3 | 9 | 270 |
| 13 | 5 | -2 | 4 | 20 | 13 | 20 | -2 | 4 | 80 |
| 14 | 30 | -1 | 1 | 30 | 14 | 10 | -1 | 1 | 10 |
| 15 | 60 | 0 | 0 | 0 | 15 | 50 | 0 | 0 | 0 |
| 16 | 30 | 1 | 1 | 30 | 16 | 10 | 1 | 1 | 10 |
| 17 | 5 | 2 | 4 | 20 | 17 | 20 | 2 | 4 | 80 |
| 18 | 1 | 3 | 9 | 9 | 18 | 30 | 3 | 9 | 270 |
| Итого | 132 | — | — | 118 | — | 170 | — | — | 720 |
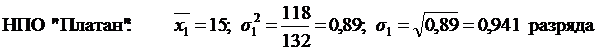 .
. На математических свойствах дисперсии основываются способы, которые позволяют упростить ее вычисление. Например, расчет дисперсии по способу моментов или способу отсчета от условного нуля применяется в вариационных рядах с равными интервалами. Расчет производится по формуле:
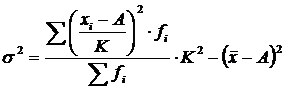 ,
,
где K – ширина интервала;
A – условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
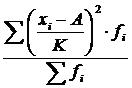 – момент второго порядка.
– момент второго порядка.
Между средним линейным и средним квадратическим отклонениями существует примерное соотношение σ=12.5·d, если фактическое распределение близко к нормальному.
В условиях нормального распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений:
1) в пределах ± 1σ располагается 68,3 % количества наблюдений;
2) в пределах ± 2σ – 95,4 %;
3) в пределах ± 3σ – 99,7 %;
В действительности, на практике почти не встречаются отклонения, которые превышают ±3σ. Отклонение 3σ может считаться максимально возможным. Это положение называют «правилом трех сигм».
Пример. Межгрупповая дисперсия равна 340, общая - 380. Определите среднюю внутригрупповую и эмпирическое корреляционное отношение.
Решение.
общая дисперсия (σ) = Межгрупповая дисперсия (δ) + средняя внутригрупповая
средняя внутригрупповая = общая дисперсия (σ) - Межгрупповая дисперсия(δ) = 380-340=40
Эмпирическое корреляционное отношение: ![]()