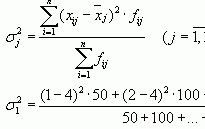Изучение формы распределения

Из математической статистики известно, что если увеличить объем совокупности и уменьшить интервал группировки, изобразить эти данные графически, по полигон (гистограмма) распределения все более приближается к некоторой плавной линии, являющейся для него пределом и носящей название кривой распределения.

Под кривой распределения понимается графическое изображение в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариант.
Получение кривой распределения на основе полигона или гистограммы можно представить лишь для гипотетического случая, соответствующего бесконечно большому числу единиц совокупности и бесконечно малой ширине интервала ряда. Только при этих идеализированных условиях кривая распределения представляет теоретическое распределение.

Теоретической кривой распределения называется кривая, выражающая общую закономерность данного типа распределения в чистом виде, исключающего влияние случайных для него закономерностей факторов. Но получение кривой распределения из эмпирических данных (полигон, гистограмма) возможно лишь для описанного идеального случая. Поэтому при проведении анализа вариационных рядов целесообразно свести эмпирическое распределение к одному из хорошо исследованных видов теоретического распределения.

Различают следующие разновидности кривых распределения:
1) одновершинные кривые: симметричные, умеренно асимметричные и крайне асимметричные;
2) многовершинные кривые.

Для однородных совокупностей, как правило, характерны одновершинные распределения. Многовершинность свидетельствует о неоднородности изучаемой совокупности. Появление двух и более вершин делает необходимой перегруппировку данных с целью выделения более однородных групп.

Выяснение общего характера распределения предполагает оценку его однородности и вычисление показателей асимметрии и эксцесса. Для симметричных распределений частоты любых двух вариант, равноотстоящих в обе стороны от центра распределения, равны между собой. Рассчитанные для таких распределений средняя, мода и медиана так же равны.
При изучении асимметрии нескольких распределений с разными единицами измерения вычисляется относительный показатель асимметрии (A_s) 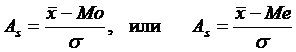, где Mo, Me – модальное (медианное) значение переменной x.
Его величина может быть положительной и отрицательной. В первом случае речь идет о правосторонней асимметрии (рис. 1), а во втором – о левосторонней (рис. 2).

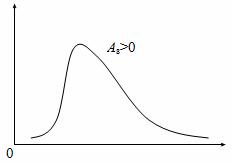
Рис. 1. Правосторонняя асимметрия

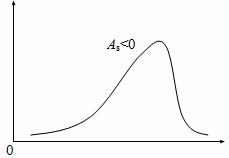
Рис. 2. Левосторонняя асимметрия

Центральными называются моменты распределения, при вычислении которых за исходную величину принимаются отклонения вариантов от средней арифметической данного ряда.
Наиболее широко в качестве показателя асимметрии применяется отношение центрального момента третьего порядка к среднему квадратическому отклонению данного ряда в кубе, т.е.:
.

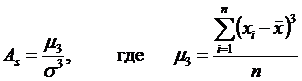Применение данного показателя дает возможность определить не только величину асимметрии, но и проверить ее наличие в генеральной совокупности. Принято считать, что асимметрия выше 0,5 (независимо от знака) считается значительной, если она меньше 0,25, то – незначительной.
Оценка существенности A_s производится коэффициента асимметрии σ_As, которая зависит от числа наблюдений n и рассчитывается по формуле:
.
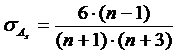В случае |A_s| / σ_As > 3 асимметрия существенна и распределение признака в генеральной совокупности несимметрично. В противном случае асимметрия несущественна, и ее наличие может быть вызвано случайными обстоятельствами.
Для симметричных распределений может быть рассчитан показатель эксцесса (E_k). Наиболее точно он определяется по формуле с использованием центрального момента четвертого порядка:
.

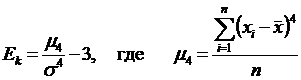Среднеквадратическая ошибка эксцесса (σ_Ek) рассчитывается по формуле:
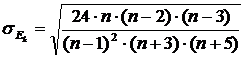, где п – число наблюдений
Для определения асимметрии и эксцесса можно пользоваться упрощенными формулами, предложенными Линдбергом:
A_s = p – 50, где p – удельный вес (в процентах) количества тех вариант, которые превосходят среднюю арифметическую, в общем количестве вариант данного ряда;
E_k = p – 38,29, где p – доля (в процентах) количества вариант, лежащих в интервале, равном половине среднего квадратического отклонения.
Хотя показатели асимметрии и эксцесса характеризуют непосредственно лишь форму распределения признака в пределах изучаемой совокупности, но их определение имеет не только описательное значение. Часто асимметрия и эксцесс дают определенные указания для дальнейшего исследования социально-экономических явлений. Так появление значительного отрицательного эксцесса может указывать на качественную неоднородность исследуемой совокупности. Кроме того, эти показатели позволяют сделать вывод о возможности применения данного эмпирического распределения к типу кривых нормального распределения.