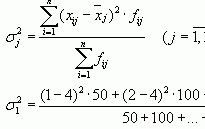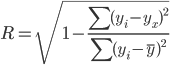Гипотеза о равенстве двух средних значений
- Гипотеза о генеральном среднем значении нормального распределения при не известной дисперсии. Предполагаем, что генеральная совокупность имеет нормальное распределение, её среднее и дисперсия неизвестны, но есть основания полагать, что генеральное среднее равно а. При уровне значимости a нужно проверить гипотезу Н0: x=a. В качестве альтернативной можно использовать одну из трёх рассмотренных выше гипотез. В данном случае статистикой служит случайная величина
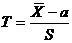 ,
,
имеющая распределение Стьюдента с n – 1 степенями свободы. Определяется соответствующее экспериментальное (наблюдаемое) значение tэкс. Из таблицы критических точек распределения Стьюдента находится критическое значение tкр. При альтернативной гипотезе Н1: x > a оно находится по уровню значимости a и числу степеней свободы n – 1. Если tэкс < tкр, то нулевая гипотеза принимается, в противоположном случае – отвергается. При альтернативной гипотезе Н1: x=a критическое значение находится по уровню значимости α/2 и том же числе степеней свободы. Нулевая гипотеза принимается, если |tэкс| < tкр. - Гипотеза о равенстве двух средних значений произвольно распределённых генеральных совокупностей (большие независимые выборки). При уровне значимости α нужно проверить гипотезу Н0: x=y. Если объём обеих выборок велик, то можно считать, что выборочные средние имеют нормальное распределение, а их дисперсии известны. В этом случае в качестве статистики можно использовать случайную величину
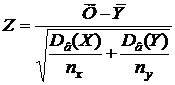 ,
,
имеющую нормальное распределение, причём M(Z) = 0, D(Z) = 1. Определяется соответствующее экспериментальное значение zэкс. Из таблицы функции Лапласа находится критическое значение zкр. При альтернативной гипотезе Н1: x > y оно находится из условия F(zкр) = 0,5 – a. Если zэкс < zкр, то нулевая гипотеза принимается, в противоположном случае – отвергается. При альтернативной гипотезе Н1: x ≠ y критическое значение находится из условия F(zкр) = 0,5×(1 – a). Нулевая гипотеза принимается, если |zэкс| < zкр. - Гипотеза о равенстве двух средних значений нормально распределённых генеральных совокупностей, дисперсии которых неизвестны и одинаковы (малые независимые выборки). При уровне значимостиaнужно проверить основную гипотезу Н0: x=y. В качестве статистики используем случайную величину
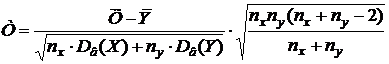 ,
,
имеющую распределение Стьюдента с (nх + nу – 2) степенями свободы. Определяется соответствующее экспериментальное значение tэкс. Из таблицы критических точек распределения Стьюдента находится критическое значение tкр. Всё решается аналогично гипотезе (I).
Пример. Доходы аптек одного из микрорайонов города за некоторый период составили 128; 192; 223; 398; 205; 266; 219; 260; 264; 98 (условных единиц). В соседнем микрорайоне за то же время они были равны 286; 240; 263; 266; 484; 223; 335.
Для обеих выборок вычислите среднее, исправленную дисперсию и среднее квадратическое отклонение. Найдите размах варьирования, среднее абсолютное (линейное) отклонение, коэффициент вариации, линейный коэффициент вариации, коэффициент осцилляции.
Предполагая, что данная случайная величина имеет нормальное распределение, определите доверительный интервал для генеральной средней (в обоих случаях).
По критерию Фишера проверьте гипотезу о равенстве генеральных дисперсий. По критерию Стьюдента проверьте гипотезу о равенстве генеральных средних (альтернативная гипотеза – об их неравенстве).
Во всех расчётах уровень значимости α = 0,05.
Решение проводим с помощью калькулятора Проверка гипотезы о равенстве дисперсий
.
1. Находим показатели вариации для первой выборки.
Проранжируем ряд. Для этого сортируем его значения по возрастанию.
Таблица для расчета показателей.
| x | |x - xср| | (x - xср)2 |
| 98 | 127.3 | 16205.29 |
| 128 | 97.3 | 9467.29 |
| 192 | 33.3 | 1108.89 |
| 205 | 20.3 | 412.09 |
| 219 | 6.3 | 39.69 |
| 223 | 2.3 | 5.29 |
| 260 | 34.7 | 1204.09 |
| 264 | 38.7 | 1497.69 |
| 266 | 40.7 | 1656.49 |
| 398 | 172.7 | 29825.29 |
| 2253 | 573.6 | 61422.1 |
Показатели центра распределения.
Простая средняя арифметическая
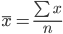
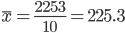
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin = 398 - 98 = 300
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
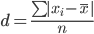
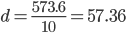
Каждое значение ряда отличается от другого в среднем на 57.36
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
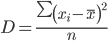
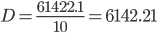
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).
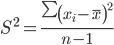
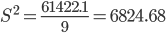
Среднее квадратическое отклонение.
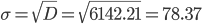
Каждое значение ряда отличается от среднего значения 225.3 в среднем на 78.37
Оценка среднеквадратического отклонения.
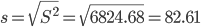
Относительные показатели вариации.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
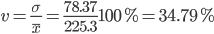
Поскольку v>30% ,но v< 70%, то вариация умеренная.
Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.
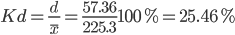
Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней.
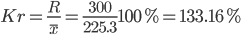
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего.
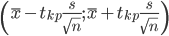
Определяем значение tkp по таблице распределения Стьюдента
По таблице Стьюдента находим:
Tтабл(n-1;α/2) = Tтабл(9;0.025) = 2.262
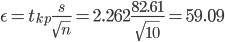
(225.3 - 59.09;225.3 + 59.09) = (166.21;284.39)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
2. Находим показатели вариации для второй выборки.
Проранжируем ряд. Для этого сортируем его значения по возрастанию.
Таблица для расчета показателей.
| x | |x - xср| | (x - xср)2 |
| 223 | 76.57 | 5863.18 |
| 240 | 59.57 | 3548.76 |
| 263 | 36.57 | 1337.47 |
| 266 | 33.57 | 1127.04 |
| 286 | 13.57 | 184.18 |
| 335 | 35.43 | 1255.18 |
| 484 | 184.43 | 34013.9 |
| 2097 | 439.71 | 47329.71 |
Простая средняя арифметическая
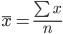
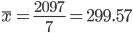
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 484 - 223 = 261
Среднее линейное отклонение - вычисляют для того, чтобы учесть различия всех единиц исследуемой совокупности.
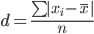
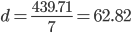
Каждое значение ряда отличается от другого в среднем на 62.82
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
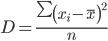
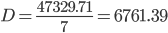
Несмещенная оценка дисперсии - состоятельная оценка дисперсии (исправленная дисперсия).
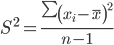
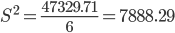
Среднее квадратическое отклонение.
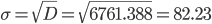
Каждое значение ряда отличается от среднего значения 299.57 в среднем на 82.23
Оценка среднеквадратического отклонения.
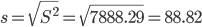
Относительные показатели вариации.
К относительным показателям вариации относят: коэффициент осцилляции, линейный коэффициент вариации, относительное линейное отклонение.
Коэффициент вариации - мера относительного разброса значений совокупности: показывает, какую долю среднего значения этой величины составляет ее средний разброс.
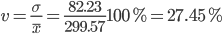
Поскольку v ≤ 30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Линейный коэффициент вариации или Относительное линейное отклонение - характеризует долю усредненного значения признака абсолютных отклонений от средней величины.
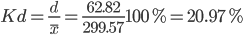
Коэффициент осцилляции - отражает относительную колеблемость крайних значений признака вокруг средней.
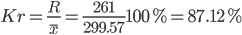
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего.
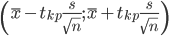
Определяем значение tkp по таблице распределения Стьюдента
По таблице Стьюдента находим:
Tтабл(n-1;α/2) = Tтабл(6;0.025) = 2.447
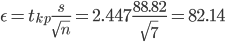
(299.57 - 82.14;299.57 + 82.14) = (217.43;381.71)
С вероятностью 0.95 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Проводим проверку гипотезы о равенстве дисперсий:
H0: Dx = Dy;
H1: Dx< Dy;
Найдём наблюдаемое значение критерия Фишера:
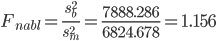
Поскольку sy2> sx2, то sб2 = sy2, sм2 = sx2
Числа степеней свободы:
f1 = nу – 1 = 7 – 1 = 6
f2 = nx – 1 = 10 – 1 = 9
По таблице критических точек распределения Фишера–Снедекора при уровне значимости α = 0.05 и данным числам степеней свободы находим Fкр(6;9) = 3.37
Т.к. Fнабл< Fкр, то нет оснований отвергать нулевую гипотезу (т.е. можно считать, что дисперсии двух выборок равны).
Проводим проверку гипотезы о равенстве генеральных средних:
H0: x=y
H1: x≠y
Найдём экспериментальное значение критерия Стьюдента:
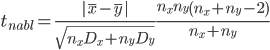

Число степеней свободы f = nх + nу – 2 = 10 + 7 – 2 = 15
Определяем значение tkp по таблице распределения Стьюдента
По таблице Стьюдента находим:
Tтабл(f;α/2) = Tтабл(15;0.025) = 2.131
По таблице критических точек распределения Стьюдента при уровне значимости α = 0.05 и данному числу степеней свободы находим tкр = 2.131
Т.к. tнабл< tкр, то нулевая гипотеза принимается, генеральные средние двух выборок равны.