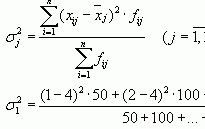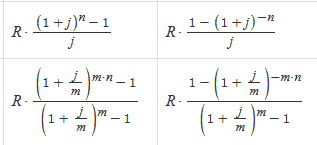Проверка гипотезы о виде распределения
назначение сервиса. С помощью онлайн-калькулятора проводится проверка статистической гипотезы по критерию согласия Пирсона
о том, что ряд имеет форму:
- нормального распределения, распределение Пуассона, биномиального распределения;
- показательного распределения (экспоненциального), равномерного распределения.
Инструкция. Чтобы провести анализ ряда, выберите вид ряда, укажите количество строк. Полученное решение сохраняется в файле Word. Иногда потребуется предварительно сгруппировать ряд, поэтому используйте калькулятор
Группировка ряда.
Для вариационного ряда:
Для интервального ряда:
Характеристики распределений
Основная задача анализа вариационных рядов – это выявление подлинной закономерности распределения, которая достигается увеличением объема исследуемой совокупности при одновременном уменьшении интервала ряда.Равномерное распределение
Графическое представление
Функция плотности равномерного распределения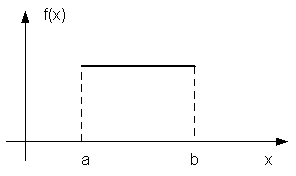 
| Математическое ожидание: M[X] = (a+b)/2
Дисперсия: 
|
Нормальное распределение
Графическое представление
Плотность распределения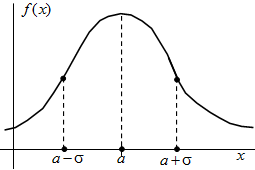 
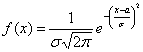
| Математическое ожидание: M[X]=a
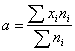
Дисперсия: D[X] = σ2
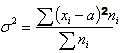
Запись Х ~ N(a; σ) означает, что случайная величина Х распределена по нормальному закону с параметрами a и σ. |
Показательное распределение
Графическое представление
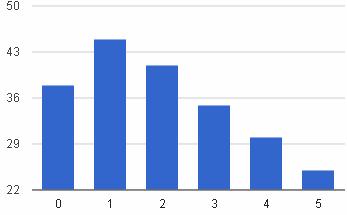
Плотность распределения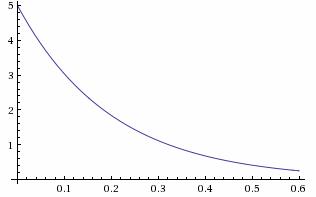 
| Математическое ожидание: M[X] = 1/λ
Дисперсия: D[X] = 1/λ2
|
Распределение Пуассона
Графическое представление
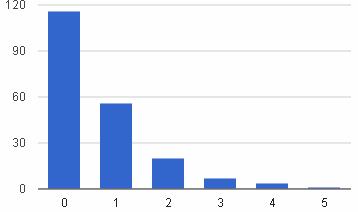
Плотность распределения Pn(i) = λie-λ/i!
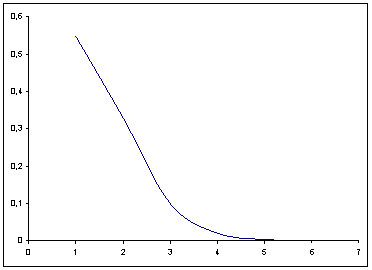
| Математическое ожидание
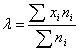
Дисперсия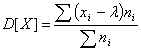 
|
Биномиальное распределение
Графическое представление
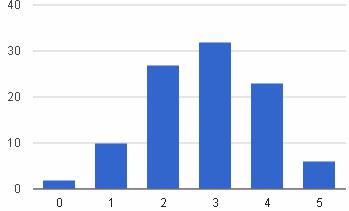
Плотность распределения биномиального распределения pi = CNipiqN-i (схема Бернулли)
| Математическое ожидание биномиального распределения
M[X] = np Дисперсия биномиального распределения D[X] = npq |
| Границы отклонений | Число деталей |
| -3..-2 | 3 |
| -2 -1 | 10 |
| -1 0 | 15 |
| 0-1 | 24 |
| 1-2 | 25 |
| 2-3 | 13 |
| 3-4 | 7 |
| 4-5 | 3 |
Пример. Имеются следующие данные о количестве заявок на автомобили технической помощи по дням. Помимо общего задания, требуется построить теоретическую кривую нормального распределения и проверить соответствие эмпирического и теоретического распределений по критерию Пирсона.
Скачать решение
Пример. Дана выборка.
10 3 7 -2 6 5 5 4 6 2 6 7 5 9 8 0 -1 9
3 2 5 5 2 1 6 9 2 4 1 7 6 -1 -5 4 2 7
3 5 5 2 11 9 7 7 4 10 5 5 6 5 7 1 6 4
2 8 4 8 5 3 6 6 8 3 7 5 8 5 6 -2 7 4
3 7 5 10 4 6 6 5 4 9 4 10 3 2 9 5 1 10
3 3 5 8 3 6 3 3 5 7
- Провести группировку данных. Число интервалов k вычислить по формуле (10*n)1/3, где n – объем выборки. Записать сгруппирированный статистический ряд распределения выборки.
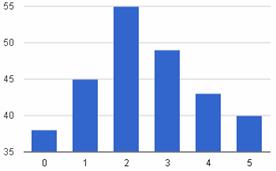
- Построить гистограмму относительных частот и выдвинуть гипотезу о законе распределения изучаемого признака Х.
- Провести проверку нулевой гипотезы, используя χ2 - критерий Пирсона при уровне значимости α=0.05. После принятия гипотезы построить график плотности распределения.
k = (10*100)1/3 = 10.
Ширина интервала составит:
h =(Xmax - Xmin)/n = (11 - (-5))/10 = 1.6
Xmax - максимальное значение группировочного признака в совокупности.
Xmin - минимальное значение группировочного признака.
Определим границы группы. Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| Номер группы | Нижняя граница | Верхняя граница |
| 1 | -5 | -3.4 |
| 2 | -3.4 | -1.8 |
| 3 | -1.8 | -0.2 |
| 4 | -0.2 | 1.4 |
| 5 | 1.4 | 3 |
| 6 | 3 | 4.6 |
| 7 | 4.6 | 6.2 |
| 8 | 6.2 | 7.8 |
| 9 | 7.8 | 9.4 |
| 10 | 9.4 | 11 |
Результаты группировки оформим в виде таблицы:
| Группы | № совокупности | Частота fi |
| -5 - -3.4 | 1 | 1 |
| -3.4 - -1.8 | 2,3 | 2 |
| -1.8 - -0.2 | 4,5 | 2 |
| -0.2 - 1.4 | 6,7,8,9,10 | 5 |
| 1.4 - 3 | 11,12,13,14,15,16,17,18,19,20,21, 22,23,24,25,26,27,28,29,30 | 20 |
| 3 - 4.6 | 31,32,33,34,35,36,37,38,39,40 | 10 |
| 4.6 - 6.2 | 41,42,43,44,45,46,47,48,49,50,51, 52,53,54,55,56,57,58, 59,60,61,62,63, 64,65,66,67,68,69,70,71 | 31 |
| 6.2 - 7.8 | 72,73,74,75,76,77,78,79,80,81,82 | 11 |
| 7.8 - 9.4 | 83,84,85,86,87,88,89,90,91,92,93,94 | 12 |
| 9.4 - 11 | 95,96,97,98,99,100 | 6 |
Таблица для расчета показателей.
| Группы | Середина интервала, xi | Кол-во, fi | xi * fi | Накопленная частота, S | (x - xср) * f | (x - xср)2 * f |
| -5 - -3.4 | -4.2 | 1 | -4.2 | 1 | 9.02 | 81.43 |
| -3.4 - -1.8 | -2.6 | 2 | -5.2 | 3 | 14.85 | 110.23 |
| -1.8 - -0.2 | -1 | 2 | -2 | 5 | 11.65 | 67.84 |
| -0.2 - 1.4 | 0.6 | 5 | 3 | 10 | 21.12 | 89.21 |
| 1.4 - 3 | 2.2 | 20 | 44 | 30 | 52.48 | 137.71 |
| 3 - 4.6 | 3.8 | 10 | 38 | 40 | 10.24 | 10.49 |
| 4.6 - 6.2 | 5.4 | 31 | 167.4 | 71 | 17.86 | 10.29 |
| 6.2 - 7.8 | 7 | 11 | 77 | 82 | 23.94 | 52.08 |
| 7.8 - 9.4 | 8.6 | 12 | 103.2 | 94 | 45.31 | 171.1 |
| 9.4 - 11 | 10.2 | 6 | 61.2 | 100 | 32.26 | 173.41 |
| 100 | 482.4 | 238.72 | 903.78 |
Показатели центра распределения.
Средняя взвешенная
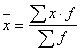
Показатели вариации.
Абсолютные показатели вариации.
Размах вариации - разность между максимальным и минимальным значениями признака первичного ряда.
R = Xmax - Xmin
R = 11 - (-5) = 16
Дисперсия - характеризует меру разброса около ее среднего значения (мера рассеивания, т.е. отклонения от среднего).
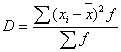
Несмещенная оценка дисперсии - состоятельная оценка дисперсии.
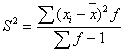
Каждое значение ряда отличается от среднего значения 4.82 не более, чем на 3.01
Оценка среднеквадратического отклонения.
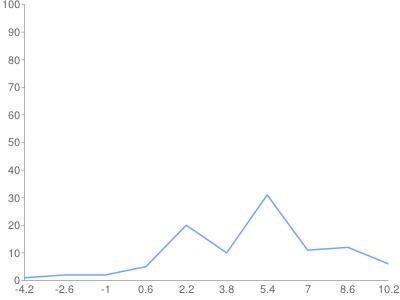
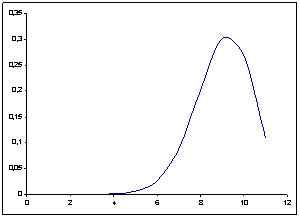
Гистограмма относительных частот (в %).
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
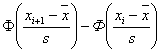
| Интервалы группировки | Наблюдаемая частота ni | Ф(xi) | Ф(xi+1) | Вероятность pi попадания в i-й интервал | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| -5 - -3,4 | 1 | 0.5 | 0.5 | 0,00276 | 0.28 | 1.9 |
| -3,4 - -1,8 | 2 | 0.49 | 0.5 | 0,0108 | 1.08 | 0.78 |
| -1,8 - -0,2 | 2 | 0.45 | 0.49 | 0,0336 | 3.36 | 0.55 |
| -0,2 - 1,4 | 5 | 0.37 | 0.45 | 0,0796 | 7.96 | 1.1 |
| 1,4 - 3 | 20 | 0.23 | 0.37 | 0,14 | 14.38 | 2.2 |
| 3 - 4,6 | 10 | 0.0319 | 0.23 | 0,2 | 19.72 | 4.79 |
| 4,6 - 6,2 | 31 | 0.18 | 0.0319 | 0,15 | 14.53 | 18.67 |
| 6,2 - 7,8 | 11 | 0.34 | 0.18 | 0,16 | 16.17 | 1.65 |
| 7,8 - 9,4 | 12 | 0.44 | 0.34 | 0,0968 | 9.68 | 0.56 |
| 9,4 - 11 | 6 | 0.48 | 0.44 | 0,0446 | 4.46 | 0.53 |
| 100 | 32.73 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = 14.06714; Kнабл = 32.73
Наблюдаемое значение статистики Пирсона попадает в критическую область: Кнабл > Kkp, поэтому есть основания отвергать основную гипотезу. Данные выборки распределены не по нормальному закону.
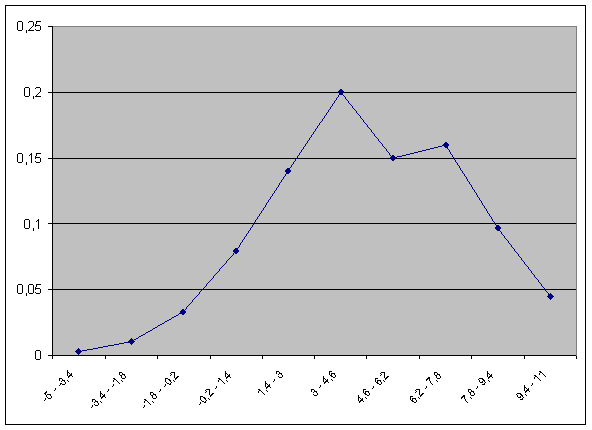
Пример
1. Нормальным или гауссовым распределением называется непрерывное распределение, плотность которого имеет вид
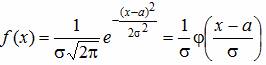
φ(x)– функция Гаусса (таблица),
Параметры a и σ имеют смысл математического ожидания и среднего квадратичного отклонения.
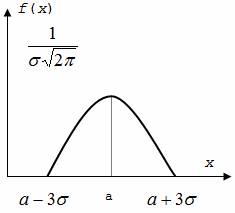
2. Справедливы формулы:
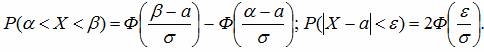
Обратим внимание, что Ф(-x)=–Ф(x), Ф(x)=0.5 при x>5.
3. Правило трех сигм: P(|X-a|>3ε)=0.0027 – т.е. вероятность отклонения нормально распределенной величины от математического ожидания более чем на 3σ практически равна нулю.
Главная особенность, выделяющая нормальный закон среди других законов распределения, состоит в том, что он является предельным, к которому приближаются другие законы при весьма часто встречающихся условиях.
Задание. Сгруппировать ряд, образовав группы с равными интервалами. Проверить ряд на нормальный закон распределения.
Решение находим с помощью калькулятора Проверка гипотезы о виде распределения
. Число групп приближенно определяется по формуле Стэрджесса
n = 1 + 3,2log n = 1 + 3,2log 57 = 7
Тогда ширина интервала составит: 
| Группы | x | Кол-во f | x * f | S | (x - x ср) * f | (x - x ср)2* f | (x - x ср)3* f | (x - x ср)4* f | Частота |
| 5.59 - 5.75 | 5.67 | 5 | 28.35 | 5 | 2.05 | 0.84 | -0.34 | 0.14 | 0.09 |
| 5.75 - 5.91 | 5.83 | 14 | 81.62 | 19 | 3.5 | 0.87 | -0.22 | 0.05 | 0.25 |
| 5.91 - 6.07 | 5.99 | 7 | 41.93 | 26 | 0.63 | 0.06 | -0.01 | 0 | 0.12 |
| 6.07 - 6.23 | 6.15 | 15 | 92.25 | 41 | 1.05 | 0.07 | 0.01 | 0 | 0.26 |
| 6.23 - 6.39 | 6.31 | 9 | 56.79 | 50 | 2.07 | 0.48 | 0.11 | 0.03 | 0.16 |
| 6.39 - 6.55 | 6.47 | 5 | 32.35 | 55 | 1.95 | 0.76 | 0.3 | 0.12 | 0.09 |
| 6.55 - 6.71 | 6.63 | 2 | 13.26 | 57 | 1.1 | 0.61 | 0.33 | 0.18 | 0.04 |
| 57 | 346.55 | 0 | 12.35 | 3.69 | 0.18 | 0.52 | 0 |
Для оценки ряда распределения найдем следующие показатели:
Показатели центра распределения.
Средняя взвешенная
Мода
Выбираем в качестве начала интервала 6.07, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 6.16
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
Таким образом, что 50% единиц совокупности будут меньше по величине 6.1
Квартили
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1 и Q2; 25% - между Q2 и Q3; остальные 25% превосходят Q3
Таким образом, что 25% единиц совокупности будут меньше по величине 5.86
Q2 совпадает с медианой, Q2 = 6.1
Остальные 25% превосходят 6.26
Децили (децентили)
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9
Таким образом, что 10% единиц совокупности будут меньше по величине 5.76
Остальные 10% превосходят 6.43
Показатели вариации.
Размах вариации
R = X max - X min
R = 6.65 - 5.59 = 1.06
Среднее линейное отклонение
Каждое значение ряда отличается от другого не более, чем на 0.22
Дисперсия
Среднее квадратическое отклонение
Каждое значение ряда отличается от среднего значения 6.08 не более, чем на 0.25
Коэффициент вариации
Поскольку v<30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять
Показатели формы распределения.
Коэффициент осцилляции
Относительное линейное отклонение
Относительный показатель квартильной вариации
Степень асимметрии
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой
Положительная величина указывает на наличие правосторонней асимметрии
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Ex > 0 - островершинное распределение
Интервальное оценивание центра генеральной совокупности
Доверительный интервал для генерального среднего
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа
В этом случае 2Ф(tkp) = 1 - γ
Ф(tkp) = γ/2 = (1- 0.05)/2 = 0.475
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 57
tkp (n-1;a) = (57;0.475) = 5
(6.08 - 0.48;6.08 + 0.48) = (5.6;6.56)
Проверка гипотез о виде распределения
Проверим это предположение с помощью критерия согласия Пирсона
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
| Интервалы группировки | Наблюдаемая частота ni | Ф(xi) | Ф(xi+1) | pi | n pi | Слагаемые статистики Пирсона Ki |
| 5.59 - 5.75 | 5 | 0.4032 | 0.4732 | 0.07 | 3.99 | 0.2556 |
| 5.75 - 5.91 | 14 | 0.2486 | 0.4032 | 0.1546 | 8.8122 | 3.0540 |
| 5.91 - 6.07 | 7 | 0.016 | 0.2486 | 0.2326 | 13.2582 | 2.9540 |
| 6.07 - 6.23 | 15 | 0.2224 | 0.016 | 0.2064 | 11.7648 | 0.8896 |
| 6.23 - 6.39 | 9 | 0.3883 | 0.2224 | 0.1659 | 9.4563 | 0.0220 |
| 6.39 - 6.55 | 5 | 0.4678 | 0.3883 | 0.0795 | 4.5315 | 0.0484 |
| 6.55 - 6.71 | 2 | 0.4934 | 0.4678 | 0.0256 | 1.4592 | 0.2004 |
| 57 | 7.424 |
Определим границу критической области. Так как статистика Пирсона измеряет разницу между эмпирическим и теоретическим распределениями, то чем больше ее наблюдаемое значение Kнабл, тем сильнее довод против основной гипотезы.
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;a) находим по таблицам распределения «хи-квадрат» и заданным значениям a, k (число интервалов), r=2 (параметры x и σ оценены по выборке).
Kkp = 9.5; Kнабл = 7.42
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.
Перейти к онлайн решению своей задачи
Пример. Длина переднего рога у африканского белого носорога описывается случайной величиной X, распределенной по нормальному закону с параметрами a=1,8 и σ2=1. Найти математическое ожидание M(5X-0,8).
см. примеры проверки гипотезы о нормальном распределении.
