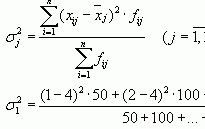Показатели вариации
Назначение сервиса. С помощью сервиса в онлайн режиме определяются следующие показатели:- средняя взвешенная, дисперсия, среднеквадратическое отклонение, мода, медиана, размах вариации;
- квартили, децили, квартильный коэффициент дифференциации, линейный коэффициент вариации, коэффициент вариации;
- среднее линейное отклонение, коэффициент осцилляции;
- характеристики формы и многие другие.
Инструкция. Чтобы рассчитать показатели вариации, выберите вид ряда, укажите количество исходных данных. Полученное решение сохраняется в файле Word. Если предварительно требуется сгруппировать ряд (т.е. построить вариационный ряд), то необходимо воспользоваться онлайн-калькулятором Группировка.
Проверка гипотезы о виде распределения ряда осуществляется через калькулятор Изучение формы распределения ряда.
Классификация показателей вариации
- К абсолютным показателям вариации относятся размах вариации, среднее линейное отклонение, дисперсия и среднеквадратическое отклонение. Вторая группа показателей вычисляется, как отношение абсолютных показателей к средней арифметической (медиане).
- Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.
| Показатель | Формула |
| Средняя арифметическая простая |  |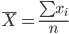
| Средняя арифметическая взвешенная |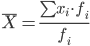 
|
| Средняя гармоническая простая |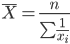 
|
| Средняя гармоническая взвешенная |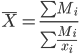 
|
| Мода |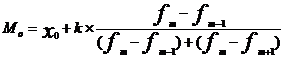 
|
| Медиана |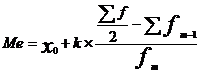 
|
| Размах вариации | R=Xmax-Xmin |
| Среднее линейное отклонение |  ;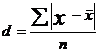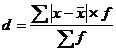 
|
| Дисперсия, Var(x) |  ;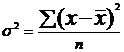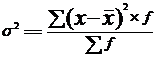 
|
| Среднее квадратическое отклонение |  |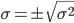
| Коэффициент вариации | 
|
| Коэффициент осцилляции | 
|
| Линейный коэффициент вариации |  |
Числовые характеристики вариационного ряда
Числовые характеристики вариационных рядов вычисляют по данным, полученным в результате наблюдений (статистическим данным), поэтому их называют также статистическими характеристиками или оценками. На практике часто оказывается достаточным знание сводных характеристик вариационных рядов: средних или характеристик положения (центральной тенденции); характеристик рассеяния или вариации (изменчивости); характеристик формы (асимметрии и крутости распределения).Самой известной и наиболее употребляемой характеристикой любого вариационного ряда является его средняя арифметическая, называемая также выборочным средним. Средняя арифметическая характеризует значения признака, вокруг которого концентрируются наблюдения, т.е. центральную тенденцию распределения. В статистическом анализе кроме средней арифметической, называемой аналитической средней, широко применяют структурные, или порядковые, средние, к которым относятся медиана и мода.
Достоинство медианы как меры центральной тенденции заключается в том, что на нее не влияет изменение крайних членов вариационного ряда, если любой из них, меньший медианы, остается меньше ее, а любой, больший медианы, продолжает быть большее ее. Медиана предпочтительнее средней арифметической для ряда, у которого крайние варианты по сравнению с остальными оказались чрезмерно большими или малыми. Особенность моды как меры центральной тенденции заключается в том, что она также не изменяется при изменении крайних членов ряда, т.е. обладает определенной устойчивостью к вариации признака.
Относительные показатели вариации
Рассмотрим показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Чаще всего относительные показатели выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % (для распределений, близких к нормальному).Различают следующие относительные показатели вариации (V):
Коэффициент осцилляции (VR):
.
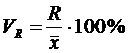Линейный коэффициент вариации (V):
.
Коэффициент вариации (Vσ):
.
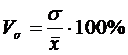Таблица - Числовые характеристики вариационного ряда
| Характеристики положения | Среднее арифметическое (выборочное среднее) | 
|
| Мода | Mo = xj, если mj = mmax | |
| Медиана | Me = xk+1, если n = 2k+1;
Me = (xk + xk+1)/2, если n = 2k | |
| Характеристики рассеяния | Выборочная дисперсия | 
|
| Выборочное среднее квадратичное отклонение |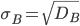 
| |
| Исправленная дисперсия |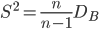 
| |
| Исправленное среднее квадратичное отклонение |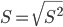 
| |
Коэффициент вариации | 
| |
| Среднее абсолютное отклонение | 
| |
| Вариационный размах | R = xmax - xmin | |
| Квартильный размах | RQ = Qв – Qн | |
| Характеристики формы | Коэффициент асимметрии | 
|
| Коэффициент эксцесса | 
|
Но наибольший интерес представляют меры вариации (рассеяния) наблюдений вокруг средних величин, в частности, вокруг средней арифметической. К таким оценкам относятся выборочная дисперсия и среднее квадратичное отклонение. Выборочная дисперсия обладает одним существенным недостатком: если среднее арифметическое выражается в тех же единицах, что и значения случайной величины, то, согласно определению, дисперсия выражается уже в квадратных единицах. Этого недостатка можно избежать, если использовать в качестве меры вариации признака среднее квадратичное отклонение. При малых объемах выборки дисперсия является смещенной оценкой, поэтому при объемах n≤30 используют исправленную дисперсию и исправленное среднее квадратичное отклонение.
Другой часто используемой характеристикой меры рассеяния признака является коэффициент вариации. Достоинством коэффициента вариации является то, что это безразмерная характеристика, позволяющая сравнивать варьирование несоизмеримых вариационных рядов. Кроме того, чем меньше значение коэффициента вариации, тем однороднее совокупность по изучаемому признаку и типичнее средняя. Совокупности с коэффициентом вариации V > 30-35% принято считать неоднородными.
Наряду с дисперсией используют и среднее абсолютное отклонение. Достоинством среднего линейного отклонения является его размерность, т.к. выражается в тех же единицах, что и значения случайной величины. Дополнительным и простым показателем рассеяния значений признака является квартильный размах. Квартильный размах включает в себя медиану и 50% наблюдений, отражающих центральную тенденцию признака, исключая наименьшие и наибольшие значения.
К характеристикам формы относят коэффициент асимметрии и эксцесс. Если коэффициент асимметрии равен нулю, то распределение имеет симметричную форму. Если распределение асимметрично, одна из ветвей полигона частот имеет более пологий спуск, чем другая. Если асимметрия правосторонняя, то справедливо неравенство: xB > Me > Mo, что означает преимущественное появление в распределении более высоких значений признака. Если асимметрия левосторонняя, то выполняется неравенство: xB < Me < Mo, означающее, что в распределении чаще встречаются более низкие значения. Чем больше значение коэффициента асимметрии, тем более асимметрично распределение (до 0,25 асимметрия незначительная; от 0,25 до 0,5 умеренная; свыше 0,5 – существенная).
Эксцесс является показателем крутости (островершинности) вариационного ряда по сравнению с нормальным распределением. Если эксцесс положителен, то полигон вариационного ряда имеет более крутую вершину. Это говорит о скоплении значений признака в центральной зоне ряда распределения, т.е. о преимущественном появлении в данных значений, близких к средней величине. Если эксцесс отрицателен - то полигон имеет более пологую вершину по сравнению с нормальной кривой. Это означает, что значения признака не концентрируются в центральной части ряда, а достаточно равномерно рассеяны по всему диапазону от минимального до максимального значения. Чем больше абсолютная величина эксцесса, тем существеннее распределение отличается от нормального.
Пример №1. 1. При выборочном изучении численности жителей в поселках городского типа получены следующие данные:
| Группы поселков с числом жителей, тыс. чел | До 3 | 3-5 | 5-10 | 10-15 | 15 и более | Итого |
| Число поселков | 26 | 25 | 35 | 11 | 13 | 100 |
Решение. В разделе «Вид статистического ряда» выбираем Интервальный ряд (рис. 1).
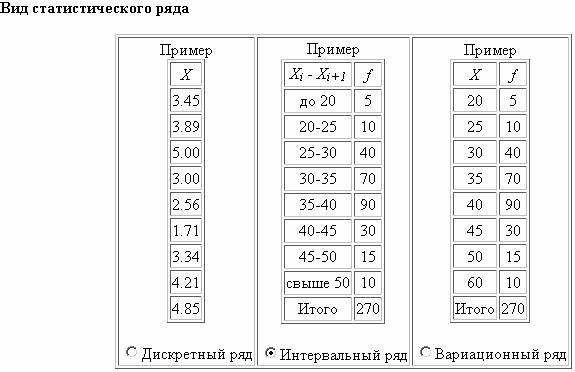
2. Поскольку в задании пять исходных строк (столбцов), то в поле Количество строк указываем 5. Нажимаем кнопку Далее.
3. На странице ввода данных заполняем исходные данные (рис. 2). При этом открытые интервалы корректируем на закрытые: из открытого интервала «до 3» формируем закрытый [1-3], из интервала «15 и более» создаем интервал [15-20].
Рисунок 3 - Гистограмма
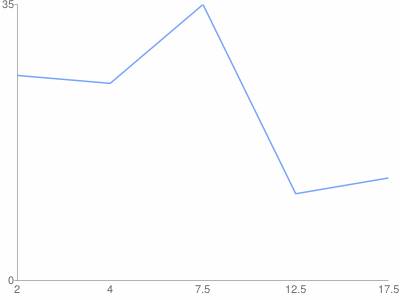
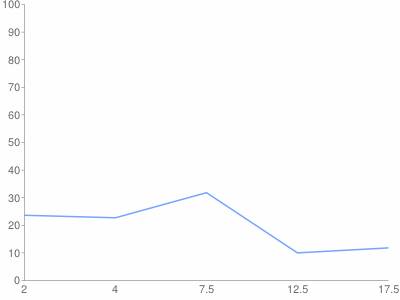
4. Нажимаем кнопку Далее. Получаем решение в формате Word (скачать) и графики (гистограмма, полигон и полигон частот).
Сводная таблица результатов имеет вид:
| Группы | x | Кол-во f | x * f | S | (x - xср) * f | (x - xср)2* f | (x - xср)3* f | (x - xср)4* f | Частота |
| 1 - 3 | 2 | 26 | 52 | 26 | 132.25 | 672.65 | -3421.33 | 17402.15 | 0.24 |
| 3 - 5 | 4 | 25 | 100 | 51 | 77.16 | 238.14 | -734.99 | 2268.45 | 0.23 |
| 5 - 10 | 7.5 | 35 | 262.5 | 86 | 14.48 | 5.99 | 2.48 | 1.02 | 0.32 |
| 10 - 15 | 12.5 | 11 | 137.5 | 97 | 59.55 | 322.38 | 1745.26 | 9448.2 | 0.1 |
| 15 - 20 | 17.5 | 13 | 227.5 | 110 | 135.38 | 1409.77 | 14680.83 | 152880.81 | 0.12 |
| 110 | 779.5 | 418.81 | 2648.93 | 12272.24 | 182000.64 | 1 |
- Второй столбец x рассчитывается как среднее значение от границ интервалов. Например, (1 + 3)/2 = 2, (3 + 5)/2 = 4.
- Пятый столбец S (кумулята) – накопленное количество f.
- Итоговое значение столбца (x-xср)*f предназначен для расчета средней взвешенной.
- Итоговое значение столбца (x-xср)2*f используется при подсчете дисперсии.
- Столбец (x-xср)3*f - для показателей асимметрии.
- Столбец (x-xср)4*f – для расчета эксцесса.
- Последний столбец (частота) рассчитывается на основании третьего столбца: 26/110 = 0.24, 25/110 = 0.23 и т.д.
По умолчанию в отчет включается расчет следующих показателей вариации:
средняя взвешенная, мода, медиана, абсолютные показатели вариации (размах вариации, среднее линейное отклонение, дисперсия, среднее квадратическое отклонение), относительные показатели вариации (коэффициент вариации, линейный коэффициент вариации).
Примечание: несмещенная оценка дисперсии и оценка среднеквадратического отклонения используются при проверке гипотезы о виде распределения, определении относительной ошибки выборки, и в случаях, когда это непосредственно требуется в задании. Во всех остальных случаях данные показатели можно исключить из отчета.
Пример №2. Для задач, где требуется предварительно сгруппировать данные, используют сервис Группировка данных
.
Число групп приближенно определяется по формуле Стэрджесса
n = 1 + 3,2log n = 1 + 3,2log 50 = 7
Тогда ширина интервала составит:
| Группы | x | Кол-во f | x * f | S | (x - x ср) * f | (x - x ср)2 * f | (x - x ср)3 * f | (x - x ср)4 * f | Частота |
| 32.11 - 37.01 | 34.56 | 1 | 34.56 | 1 | 17.35 | 300.88 | -5219.13 | 90531.01 | 0.02 |
| 37.01 - 41.91 | 39.46 | 5 | 197.31 | 6 | 62.23 | 774.51 | -9639.61 | 119974.57 | 0.1 |
| 41.91 - 46.81 | 44.36 | 6 | 266.17 | 12 | 45.28 | 341.65 | -2578.11 | 19454.43 | 0.12 |
| 46.81 - 51.71 | 49.26 | 12 | 591.14 | 24 | 31.75 | 84.02 | -222.31 | 588.22 | 0.24 |
| 51.71 - 56.61 | 54.16 | 11 | 595.78 | 35 | 24.79 | 55.89 | 125.97 | 283.93 | 0.22 |
| 56.61 - 61.51 | 59.06 | 10 | 590.62 | 45 | 71.54 | 511.8 | 3661.4 | 26193.63 | 0.2 |
| 61.51 - 66.41 | 63.96 | 5 | 319.81 | 50 | 60.27 | 726.49 | 8757.17 | 105558.87 | 0.1 |
| 50 | 2595.39 | 0 | 313.21 | 2795.24 | -5114.63 | 362584.66 | 1 |
Для оценки ряда распределения найдем следующие показатели:
Показатели центра распределения.
Средняя взвешенная
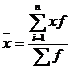
Мода
Выбираем в качестве начала интервала 46.81189, так как именно на этот интервал приходится наибольшее количество
Наиболее часто встречающееся значение ряда – 51.01
Медиана
Медиана делит выборку на две части: половина вариант меньше медианы, половина — больше
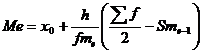
Таким образом, 50% единиц совокупности будут меньше по величине 52.16
Квартили
Квартили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 25% единиц совокупности будут меньше по величине Q1; 25% будут заключены между Q1 и Q2; 25% - между Q2 и Q3; остальные 25% превосходят Q3
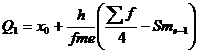
Таким образом, 25% единиц совокупности будут меньше по величине 47.02
Q2 совпадает с медианой, Q2 = 52.16
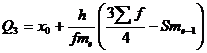
Остальные 25% превосходят значение 57.84.
Квартильный коэффициент дифференциации.
k = Q1 / Q3
k = 47.02 / 57.84 = 0.81
Децили (децентили)
Децили – это значения признака в ранжированном ряду распределения, выбранные таким образом, что 10% единиц совокупности будут меньше по величине D1; 80% будут заключены между D1 и D9; остальные 10% превосходят D9
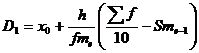
Таким образом, 10% единиц совокупности будут меньше по величине 40.93
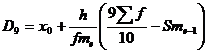
Остальные 10% превосходят 61.51
Расчет показателей вариации
Размах вариацииR = Xmax - Xmin
R = 66.39923 - 32.11189 = 34.29
Среднее линейное отклонение
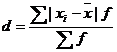
Каждое значение ряда отличается от другого не более, чем на 6.26
Дисперсия
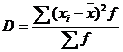
Несмещенная оценка дисперсии.
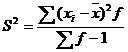
Среднее квадратическое отклонение.
Каждое значение ряда отличается от среднего значения 51.91 не более, чем на 7.48
Оценка среднеквадратического отклонения.
Коэффициент вариации
Поскольку v<30%, то совокупность однородна, а вариация слабая. Полученным результатам можно доверять.
Показатели формы распределения.
Коэффициент осцилляции
Относительное линейное отклонение
Относительный показатель квартильной вариации
Степень асимметрии
Симметричным является распределение, в котором частоты любых двух вариантов, равностоящих в обе стороны от центра распределения, равны между собой.
Отрицательный знак свидетельствует о наличии левосторонней асимметрии
Для симметричных распределений рассчитывается показатель эксцесса (островершинности). Эксцесс представляет собой выпад вершины эмпирического распределения вверх или вниз от вершины кривой нормального распределения.
Ex > 0 - островершинное распределение
Интервальное оценивание центра генеральной совокупности.
Доверительный интервал для генерального среднего
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа
В этом случае 2Ф(tkp) = 1 - γ
Ф(tkp) = (1 - γ)/2 = 0.954/2 = 0.477
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.477
tkp (γ) = (0.477) = 2
(51.91 - 2.13;51.91 + 2.13) = (49.77789;54.03789)
С вероятностью 0.954 можно утверждать, что среднее значение при выборке большего объема не выйдет за пределы найденного интервала.
Доверительный интервал для дисперсии.
Вероятность выхода за нижнюю границу равна 0.05 / 2 = 0.025. Для количества степеней свободы k = 49, по таблице распределения хи-квадрат находим:
χ2(49) = 46.97924
Случайная ошибка дисперсии:
(57.05 – 7,87; 57.05 + 7,87)
(49.18; 64.92)
Интервальное оценивание генеральной доли (вероятности события).
Доверительный интервал для генеральной доли.
Поскольку n>30, то определяем значение tkp по таблицам функции Лапласа
В этом случае 2Ф(tkp) = 1 - γ
Ф(tkp) = (1 - γ)/2 = 0.954/2 = 0.477
По таблице функции Лапласа найдем, при каком tkp значение Ф(tkp) = 0.477
tkp (γ) = (0.477) = 2
| Доля i-ой группы fi / ∑f | Средняя ошибка выборки для генеральной доли, ε | Нижняя граница доли, p* + ε | Верхняя граница доли, p* + ε |
| 0.02 | 
| 0.0002 | 0.0398 |
| 0.1 | 
| 0.0576 | 0.14 |
| 0.12 | 
| 0.074 | 0.17 |
| 0.24 | 
| 0.18 | 0.3 |
| 0.22 | 
| 0.16 | 0.28 |
| 0.2 | 
| 0.14 | 0.26 |
| 0.1 |
| 0.0576 | 0.14 |
Проверка гипотез о виде распределения.
1. Проверим гипотезу о том, что Х распределено по нормальному закону с помощью критерия согласия Пирсона.
где pi — вероятность попадания в i-й интервал случайной величины, распределенной по гипотетическому закону
Для вычисления вероятностей pi применим формулу и таблицу функции Лапласа
| Интервалы группировки | Наблюдаемая частота ni | Ф(xi) | Ф(xi+1) | Вероятность pi попадания в i-й интервал | Ожидаемая частота npi | Слагаемые статистики Пирсона Ki |
| 32.11 - 37.01 | 1 | 0.48 | 0.5 | 0.0198 | 0.99 | 0.0001 |
| 37.01 - 41.91 | 5 | 0.41 | 0.48 | 0.0679 | 3.4 | 0.76 |
| 41.91 - 46.81 | 6 | 0.25 | 0.41 | 0.16 | 7.83 | 0.43 |
| 46.81 - 51.71 | 12 | 0.012 | 0.25 | 0.24 | 11.99 | 0 |
| 51.71 - 56.61 | 11 | 0.24 | 0.012 | 0.22 | 11.19 | 0.003 |
| 56.61 - 61.51 | 10 | 0.4 | 0.24 | 0.16 | 8.2 | 0.4 |
| 61.51 - 66.41 | 5 | 0.47 | 0.4 | 0.0735 | 3.68 | 0.48 |
| 0 | 50 | 0 | 0 | 0 | 0 | 2.06 |
Поэтому критическая область для этой статистики всегда правосторонняя: [Kkp;+∞).
Её границу Kkp = χ2(k-r-1;α) находим по таблицам распределения «хи-квадрат» и заданным значениям s, k (число интервалов), r=2 (параметры xcp и s оценены по выборке).
Kkp = 9.5; Kнабл = 2.06
Наблюдаемое значение статистики Пирсона не попадает в критическую область: Кнабл < Kkp, поэтому нет оснований отвергать основную гипотезу. Справедливо предположение о том, что данные выборки имеют нормальное распределение.
Пример №3. Для изучения явления проведена 5%-ная механическая выборка. Определить;
- по выборке:
- среднее значение;
- моду и медиану;
- показатели вариации: размах вариации, среднее линейное отклонение, среднее квадратическое отклонение, коэффициент вариации;
- с вероятностью 0.954 пределы, в которых можно ожидать среднюю и долю более 1,5 лет;
- необходимую численность выборки при определении средней, чтобы с вероятностью 0.997 предельная ошибка выборки не превысила 3.
Типы вариации
Вариация – колеблемость или изменяемость величин признака у единиц совокупности.Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям.
Под вариацией во времени подразумевают изменение значений признака в различные моменты времени. Так, со временем изменяются средняя продолжительность жизни, мнения людей и т.д.
Меры вариации
Колеблемость или изменяемость величин признака у единиц совокупности называется вариацией.Вариация порождается комплексом условий, действующих на совокупность и ее единицы. Например, вариация оценок на экзамене в вузе порождается различными способностями студентов, неодинаковым временем, затрачиваемым на самостоятельную работу, различием социально-бытовых условий и т.д.
Вариация существует и в пространстве и во времени.
Под вариацией в пространстве понимается колеблемость значений признака по отдельным территориям.
Под вариацией во времени подразумевают изменение значений признака в различные моменты времени. Так, со временем изменяются средняя продолжительность жизни, мнения людей и т.д.
Показатели вариации делятся на две группы: абсолютные и относительные.
К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднеквадратическое отклонение. Вторая группа показателей вычисляется, как отношение абсолютных показателей к средней арифметической (медиане).
Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.
Простой абсолютный показатель - размах вариации (R). Размах вариации рассчитывается как разность между наибольшим (Xmax) и наименьшим (Xmin) значениями варьирующего признака, т.е. R=Xmax-Xmin..
Прежде, чем определить величину размаха вариации необходимо очистить совокупность от аномальных наблюдений.
Например, нельзя вычислять размах вариации работников какого-либо частного предприятия, если наряду с заработками его работников включен заработок его владельца.
Размах вариации – важный показатель колеблемости признака, но не исчерпывающий его характеристику.
Рассмотрим среднее линейное отклонение. Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант xi от по формуле:
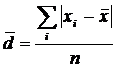(простая средняя),
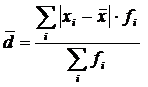(взвешенная средняя).
Покажем расчет среднего линейного отклонения на следующем примере (табл.).
Таблица - Группировка промышленных фирм по вооруженности работников промышленно-производственными основными фондами одного из регионов России.
| Группы фирм по величине ППОФ на одного работника, млн. руб., x | Среднегодовая численность ППП в % к итогу, fi | Середина интервалов, x | x·f | |x-x| | |x-x|·fi |
| А | 1 | 2 | 3 | 4 | 5 |
| До 1,0 | 7,8 | 0,5 | 3,90 | 6,16 | 48,048 |
| 1,1 – 2,0 | 12,2 | 1,5 | 18,30 | 5,16 | 62,952 |
| 2,1 – 3,0 | 14,9 | 2,5 | 37,25 | 4,16 | 61,984 |
| 3,1 – 5,0 | 23,3 | 4,0 | 93,20 | 2,66 | 61,978 |
| 5,1 – 10,0 | 24,3 | 7,5 | 182,25 | 0,84 | 20,413 |
| 10,1 –20,0 | 10,6 | 15,0 | 159,00 | 8,34 | 88,404 |
| 20,1 и более | 25,0 | 25,0 | 172,50 | 18,34 | 126,546 |
| ИТОГО | 100,0 | — | 666,40 | — | 470,324 |
Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности. Если возведем все отклонения признака во вторую степень, то получим меру вариации, которая называется дисперсией, а корень квадратный из дисперсии
– средним квадратическим отклонением (σ). Эти показатели являются общепринятыми мерами вариации.
Принципы определения показателей вариации
Для ранжированного ряда показатели вариации определяются по простым формулам (например, средняя величина определяется по формуле средней арифметической простой). Для вариационных рядов показатели вариации определяются по агрегатным формулам (с использованием частот). В этом случае показатели вариации являются взвешенными (например, взвешенная средняя).Пример №4. Средние величины и показатели вариации имеют в статистике важное значение. Они широко применяются для характеристики статистических совокупностей по варьирующим признакам.
В задачах контрольных работ могут приводиться так называемые открытые интервалы, то есть, интервалы, у которых верхняя или нижняя границы точно не определены, а сама граница остается как бы открытой. В этом случае за величину открытого интервала условно принимается величина смежного закрытого интервала. Например, дан вариационный ряд распределения работников магазина:
| Группы работающих по величине заработка (руб. в месяц) | Число работающих (чел.) |
| до 8000 | 6 |
| от 8000 до 9000 | 10 |
| от 9000 до 10000 | 14 |
| и т.д. |
При определении среднего квадратического отклонения при достаточно большом объеме изучаемой совокупности (n > 30) применяются формулы:
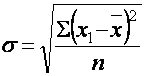(2) – среднее квадратическое отклонение простое (или невзвешенное);
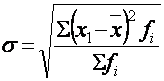(3) – среднее квадратическое отклонение взвешенное, где:
xi – значения изучаемого признака (варианты);
n – объем статистической совокупности;
x – средняя арифметическая величина.