Интервальное оценивание генеральной доли
Интервальное оценивание вероятности события. Формулы расчета численности выборки при собственно-случайном способе отбора.Для определения вероятностей интересующих нас событий мы применяем выборочный метод: проводим n независимых экспериментов, в каждом из которых может произойти (или не произойти) событие А (вероятность р появления события А в каждом эксперименте постоянна). Тогда относительная частота p* появлений событий А в серии из n испытаний принимается в качестве точечной оценки для вероятности p появления события А в отдельном испытании. При этом величину p* называют выборочной долей появлений события А, а р — генеральной долей.
В силу следствия из центральной предельной теоремы (теорема Муавра-Лапласа) относительную частоту события при большом объеме выборки можно считать нормально распределенной с параметрами M(p*)=p и 
Поэтому при n>30 доверительный интервал для генеральной доли можно построить, используя формулы:
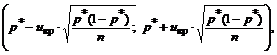
где uкр находится по таблицам функции Лапласа с учетом заданной доверительной вероятности γ: 2Ф(uкр)=γ.
При малом объеме выборки n≤30 предельная ошибка ε определяется по таблице распределения Стьюдента:
где tкр=t(k; α) и число степеней свободы k=n-1 вероятность α=1-γ (двустороння область).
Формулы справедливы, если отбор проводился случайным повторным образом (генеральная совокупность бесконечна), в противном случае необходимо сделать поправку на бесповторность отбора (таблица).
Средняя ошибка выборки для генеральной доли
| Генеральная совокупность | Бесконечная | Конечная объема N |
| Тип отбора | Повторный | Бесповторный |
| Средняя ошибка выборки | 
| 
|
Формулы расчета численности выборки при собственно-случайном способе отбора
| Способ отбора | Формулы определения численности выборки | ||
| для средней | для доли | ||
| Повторный | 
| 
| |
| Бесповторный | 
| 
| |
Задачи о генеральной доле
На вопрос «Накрывает ли доверительный интервал заданное значение p0?» — можно ответить, проверив статистическую гипотезу H0:p=p0. При этом предполагается, что опыты проводятся по схеме испытаний Бернулли (независимы, вероятность p появления события А постоянна). По выборке объема n определяют относительную частоту p* появления события A:
где m — количество появлений события А в серии из n испытаний. Для проверки гипотезы H0 используется статистика, имеющая при достаточно большом объеме выборки стандартное нормальное распределение (табл. 1).
Таблица 1 - Гипотезы о генеральной доле
Гипотеза | H0:p=p0 | H0:p1=p2 |
| Предположения | Схема испытаний Бернулли | Схема испытаний Бернулли |
| Оценки по выборке |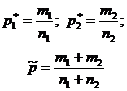 
| 
|
| Статистика K |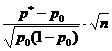 
| 
|
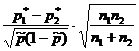
| Распределение статистики K | Стандартное нормальное N(0,1) | Стандартное нормальное N(0,1) |
Пример №1. С помощью случайного повторного отбора руководство фирмы провело выборочный опрос 900 своих служащих. Среди опрошенных оказалось 270 женщин. Постройте доверительный интервал, с вероятностью 0.95 накрывающий истинную долю женщин во всем коллективе фирмы.
Решение. По условию выборочная доля женщин составляет 
(относительная частота женщин среди всех опрошенных). Так как отбор является повторным, и объем выборки велик (n=900) предельная ошибка выборки определяется по формуле
Значение uкр находим по таблице функции Лапласа из соотношения 2Ф(uкр)=γ, т.е. 
Функция Лапласа (приложение 1) принимает значение 0.475 при uкр=1.96. Следовательно, предельная ошибка 
и искомый доверительный интервал
(p – ε, p + ε) = (0.3 – 0.18; 0.3 + 0.18) = (0.12; 0.48)
Итак, с вероятностью 0.95 можно гарантировать, что доля женщин во всем коллективе фирмы находится в интервале от 0.12 до 0.48.
Пример №2. Владелец автостоянки считает день «удачным», если автостоянка заполнена более, чем на 80 %. В течение года было проведено 40 проверок автостоянки, из которых 24 оказались «удачными». С вероятностью 0.98 найдите доверительный интервал для оценки истинной доли «удачных» дней в течение года.
Решение. Выборочная доля «удачных» дней составляет 
По таблице функции Лапласа найдем значение uкр при заданной
доверительной вероятности 
Ф(2.23) = 0.49, uкр = 2.33.
Считая отбор бесповторным (т.е. две проверки в один день не проводилось), найдем предельную ошибку: 
где n=40, N = 365 (дней). Отсюда 
и доверительный интервал для генеральной доли: (p – ε, p + ε) = (0.6 – 0.17; 0.6 + 0.17) = (0.43; 0.77)
С вероятностью 0.98 можно ожидать, что доля «удачных» дней в течение года находится в интервале от 0.43 до 0.77.
Пример №3. Проверив 2500 изделий в партии, обнаружили, что 400 изделий высшего сорта, а n–m – нет. Сколько надо проверить изделий, чтобы с уверенностью 95% определить долю высшего сорта с точностью до 0.01?
Решение ищем по формуле определения численности выборки для повторного отбора.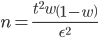
Ф(t) = γ/2 = 0.95/2 = 0.475 и этому значению по таблице Лапласа соответствует t=1.96
Выборочная доля w = 0.16; ошибка выборки ε = 0.01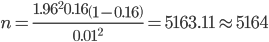
Пример №4. Партия изделий принимается, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0.97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости α=0,02 принять партию?
Решение. Сформулируем основную и альтернативную гипотезы.
H0:p=p0=0,97 — неизвестная генеральная доля p равна заданному значению p0=0,97. Применительно к условию — вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0.97; т.е. партию изделий можно принять.
H1:p<0,97 - вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0.97; т.е. партию изделий нельзя принять. При такой альтернативной гипотезе критическая область будет левосторонней.
Наблюдаемое значение статистики K (таблица) вычислим при заданных значениях p0=0,97, n=200, m=193
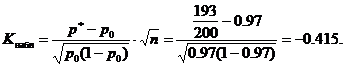
Критическое значение находим по таблице функции Лапласа из равенства
По условию α=0,02 отсюда Ф(Ккр)=0,48 и Ккр=2,05. Критическая область левосторонняя, т.е. является интервалом (-∞;-Kkp)= (-∞;-2,05). Наблюдаемое значение Кнабл=-0,415 не принадлежит критической области, следовательно, на данном уровне значимости нет оснований отклонять основную гипотезу. Партию изделий принять можно.
Пример №5. Два завода изготавливают однотипные детали. Для оценки их качества сделаны выборки из продукции этих заводов и получены следующие результаты. Среди 200 отобранных изделий первого завода оказалось 20 бракованных, среди 300 изделий второго завода — 15 бракованных.
На уровне значимости 0.025 выяснить, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей.
Решение. Это задача о сравнении генеральных долей двух совокупностей. Сформулируем основную и альтернативную гипотезы.
H0:p1=p2 — генеральные доли равны. Применительно к условию — вероятность появления бракованного изделия в продукции первого завода равна вероятности появления бракованного изделия в продукции второго завода (качество продукции одинаково).
H0:p1≠p2 — заводы изготавливают детали разного качества.
Для вычисления наблюдаемого значения статистики K (таблица) рассчитаем оценки по выборке.
Наблюдаемое значение равно
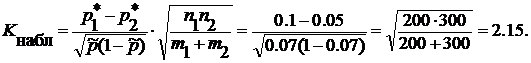
По условию α=0,025 отсюда Ф(Ккр)=0,4875 и Ккр=2,24. При двусторонней альтернативе область допустимых значений имеет вид (-2,24;2,24). Наблюдаемое значение Kнабл=2,15 попадает в этот интервал, т.е. на данном уровне значимости нет оснований отвергать основную гипотезу. Заводы изготавливают изделия одинакового качества.
