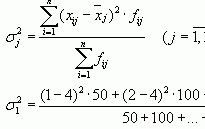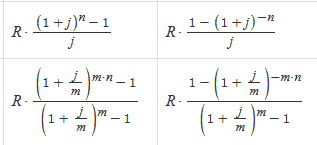Пример нахождения межгрупповой дисперсии
Межгрупповая дисперсия относится на счет изучаемого фактора, она называется факторной. Находится как сумма квадратов отклонений разности средней каждой группы (yi) от общей средней (y):
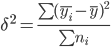
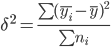
Пример. Для решения используют калькулятор. Данные группируются по признаку-фактору. Затем по каждой группе рассчитывается среднее значение. Задача состоит в том, чтобы увидеть, есть связь между признаками или нет; прямая связь или обратная; линейная или нелинейная.
Число групп приближенно определяется по формуле Стэрджесса
n = 1 + 3,2log n = 1 + 3,2log 30 = 6
Тогда ширина интервала составит: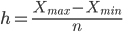
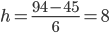
Для каждого значения ряда подсчитаем, какое количество раз оно попадает в тот или иной интервал. Для этого сортируем ряд по возрастанию.
| 45 | 45 - 53 | 1 |
| 48 | 45 - 53 | 2 |
| 50 | 45 - 53 | 3 |
| 50 | 45 - 53 | 4 |
| 55 | 53 - 61 | 1 |
| 60 | 53 - 61 | 2 |
| 63 | 61 - 69 | 1 |
| 64 | 61 - 69 | 2 |
| 64 | 61 - 69 | 3 |
| 65 | 61 - 69 | 4 |
| 66 | 61 - 69 | 5 |
| 66 | 61 - 69 | 6 |
| 68 | 61 - 69 | 7 |
| 70 | 69 - 77 | 1 |
| 70 | 69 - 77 | 2 |
| 75 | 69 - 77 | 3 |
| 76 | 69 - 77 | 4 |
| 77 | 69 - 77 | 5 |
| 78 | 77 - 85 | 1 |
| 80 | 77 - 85 | 2 |
| 80 | 77 - 85 | 3 |
| 80 | 77 - 85 | 4 |
| 80 | 77 - 85 | 5 |
| 86 | 85 - 93 | 1 |
| 87 | 85 - 93 | 2 |
| 88 | 85 - 93 | 3 |
| 88 | 85 - 93 | 4 |
| 90 | 85 - 93 | 5 |
| 90 | 85 - 93 | 6 |
| 94 | 85 - 93 | 7 |
| Группы | № | Кол-во, f | ∑X | X=∑X / f | ∑Y | Y=∑Y / f |
| 45 - 53 | 1,2,3,4 | 4 | 193 | 48.25 | 73 | 18.25 |
| 53 - 61 | 5,6 | 2 | 115 | 57.5 | 49 | 24.5 |
| 61 - 69 | 7,8,9,10,11,12,13 | 7 | 456 | 65.14 | 137 | 19.57 |
| 69 - 77 | 14,15,16,17,18 | 5 | 368 | 73.6 | 134 | 26.8 |
| 77 - 85 | 19,20,21,22,23 | 5 | 398 | 79.6 | 162 | 32.4 |
| 85 - 93 | 24,25,26,27,28,29,30 | 7 | 623 | 89 | 270 | 38.57 |
| Итого | 30 | 2153 | 825 |
1. Находим средние значения каждой группы.
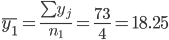
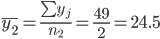
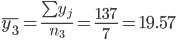
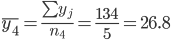
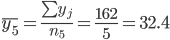
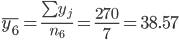
Общее средние значение для всей совокупности:
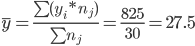
2. Дисперсия внутри группы при относительном постоянстве признака-фактора возникает за счет других факторов (не связанных с изучением). Эта дисперсия называется остаточной:
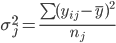
Расчет для группы: 45 - 53 (1,2,3,4)
| yj | (yj - y1)2 | Результат |
| 15 | (15 - 18.25)2 | 10.56 |
| 25 | (25 - 18.25)2 | 45.56 |
| 15 | (15 - 18.25)2 | 10.56 |
| 18 | (18 - 18.25)2 | 0.0625 |
| Итого | 66.75 |
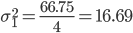
Расчет для группы: 53 - 61 (5,6)
| yj | (yj - y2)2 | Результат |
| 20 | (20 - 24.5)2 | 20.25 |
| 29 | (29 - 24.5)2 | 20.25 |
| Итого | 40.5 |
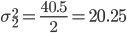
Расчет для группы: 61 - 69 (7,8,9,10,11,12,13)
| yj | (yj - y3)2 | Результат |
| 19 | (19 - 19.57)2 | 0.33 |
| 18 | (18 - 19.57)2 | 2.47 |
| 18 | (18 - 19.57)2 | 2.47 |
| 21 | (21 - 19.57)2 | 2.04 |
| 20 | (20 - 19.57)2 | 0.18 |
| 20 | (20 - 19.57)2 | 0.18 |
| 21 | (21 - 19.57)2 | 2.04 |
| Итого | 9.71 |
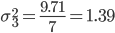
Расчет для группы: 69 - 77 (14,15,16,17,18)
| yj | (yj - y4)2 | Результат |
| 21 | (21 - 26.8)2 | 33.64 |
| 22 | (22 - 26.8)2 | 23.04 |
| 33 | (33 - 26.8)2 | 38.44 |
| 32 | (32 - 26.8)2 | 27.04 |
| 26 | (26 - 26.8)2 | 0.64 |
| Итого | 122.8 |
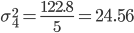
Расчет для группы: 77 - 85 (19,20,21,22,23)
| yj | (yj - y5)2 | Результат |
| 25 | (25 - 32.4)2 | 54.76 |
| 29 | (29 - 32.4)2 | 11.56 |
| 38 | (38 - 32.4)2 | 31.36 |
| 28 | (28 - 32.4)2 | 19.36 |
| 42 | (42 - 32.4)2 | 92.16 |
| Итого | 209.2 |
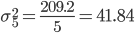
Расчет для группы: 85 - 93 (24,25,26,27,28,29,30)
| yj | (yj - y6)2 | Результат |
| 35 | (35 - 38.57)2 | 12.76 |
| 36 | (36 - 38.57)2 | 6.61 |
| 35 | (35 - 38.57)2 | 12.76 |
| 42 | (42 - 38.57)2 | 11.76 |
| 38 | (38 - 38.57)2 | 0.33 |
| 38 | (38 - 38.57)2 | 0.33 |
| 46 | (46 - 38.57)2 | 55.18 |
| Итого | 99.71 |
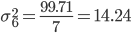
3. Внутригрупповые дисперсии объединяются в средней величине внутригрупповых дисперсий:
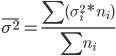
Средняя из частных дисперсий:
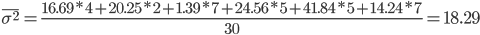
4. Межгрупповая дисперсия относится на счет изучаемого фактора, она называется факторной:
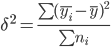
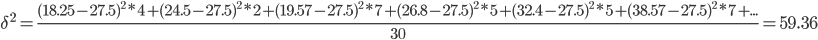
σ2=σ²i+δ2
σ2 = 18.29 + 59.36 = 77.65
Проверим этот вывод путем расчета общей дисперсии обычным способом:
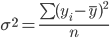
| yi | (yi - y)2 | Результат |
| 15 | (15 - 27.5)2 | 156.25 |
| 25 | (25 - 27.5)2 | 6.25 |
| 15 | (15 - 27.5)2 | 156.25 |
| 18 | (18 - 27.5)2 | 90.25 |
| 20 | (20 - 27.5)2 | 56.25 |
| 29 | (29 - 27.5)2 | 2.25 |
| 19 | (19 - 27.5)2 | 72.25 |
| 18 | (18 - 27.5)2 | 90.25 |
| 18 | (18 - 27.5)2 | 90.25 |
| 21 | (21 - 27.5)2 | 42.25 |
| 20 | (20 - 27.5)2 | 56.25 |
| 20 | (20 - 27.5)2 | 56.25 |
| 21 | (21 - 27.5)2 | 42.25 |
| 21 | (21 - 27.5)2 | 42.25 |
| 22 | (22 - 27.5)2 | 30.25 |
| 33 | (33 - 27.5)2 | 30.25 |
| 32 | (32 - 27.5)2 | 20.25 |
| 26 | (26 - 27.5)2 | 2.25 |
| 25 | (25 - 27.5)2 | 6.25 |
| 29 | (29 - 27.5)2 | 2.25 |
| 38 | (38 - 27.5)2 | 110.25 |
| 28 | (28 - 27.5)2 | 0.25 |
| 42 | (42 - 27.5)2 | 210.25 |
| 35 | (35 - 27.5)2 | 56.25 |
| 36 | (36 - 27.5)2 | 72.25 |
| 35 | (35 - 27.5)2 | 56.25 |
| 42 | (42 - 27.5)2 | 210.25 |
| 38 | (38 - 27.5)2 | 110.25 |
| 38 | (38 - 27.5)2 | 110.25 |
| 46 | (46 - 27.5)2 | 342.25 |
| Итого | 2329.5 |
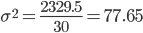
Эмпирическое корреляционное отношение измеряет, какую часть общей колеблемости результативного признака вызывает изучаемый фактор. Это отношение факторной дисперсии к общей дисперсии:
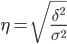
Определяем эмпирическое корреляционное отношение:
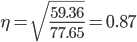
Связи между признаками могут быть слабыми и сильными (тесными). Их критерии оцениваются по шкале Чеддока:
0.1 < η < 0.3: слабая;
0.3 < η < 0.5: умеренная;
0.5 < η < 0.7: заметная;
0.7 < η < 0.9: высокая;
0.9 < η < 1: весьма высокая;
В нашем примере связь между признаком Y фактором X высокая
Коэффициент детерминации.
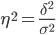
Определим коэффициент детерминации:
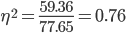
Таким образом, на 76.45% вариация обусловлена различиями между признаками, а на 23.55% – другими факторами.