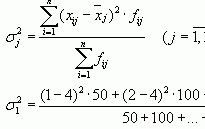Критические точки распределения Χ2
Пусть U1, U2, ..,Uk — независимые стандартные нормальные величины. Распределение случайной величины K = U12+U22 + .. + Uk2 называется распределением «хи-квадрат» с k степенями свободы (пишут K~χ2(k)). Это унимодальное распределение с положительной асимметрией и следующими характеристиками: мода M=k-2 математическое ожидание m=k дисперсия D=2k (рис.). При достаточно большом значении параметра k распределение χ2(k) имеет приближенно нормальное распределение с параметрамиПри решении задач математической статистики используются критические точки χ2(k) зависящие от заданной вероятности α и числа степеней свободы k (приложение 2). Критическая точка Χ2кр=Χ2(k; α) является границей области, правее которой лежит 100- α % площади под кривой плотности распределения. Вероятность того, что значение случайной величины K~χ2(k)при испытаниях попадет правее точки χ2(k) не превышает α P(K≥χ2kp)≤ α). Например, для случайной величины K~χ2(20) зададим вероятность α=0.05. По таблице критических точек распределения «хи-квадрат» (таблицы) находим χ2kp = χ2(20;0.05)=31.4. Значит, вероятность этой случайной величине K принять значение, большее 31.4, меньше 0.05 (рис.).
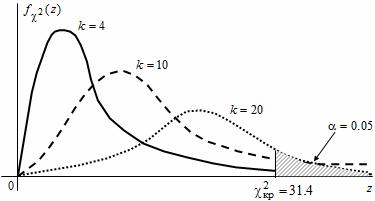
Рис. График плотности распределения χ2(k)при различных значениях числа степеней свободы k
Критические точки χ2(k) используются в следующих калькуляторах:
- Проверка гипотезы о виде распределения.
- Коэффициент контингенции.
- Коэффициент конкордации.
- Проверка наличия мультиколлинеарности (о мультиколлинеарности).
Поэтому для проверки направления связи выбирается корреляционный анализ, в частности проверка гипотезы при помощи коэффициента корреляции Пирсона с дальнейшей проверкой на достоверность при помощи t-критерия.
Для любого значения уровня значимости α Χ2 можно найти с помощью функции MS Excel: =ХИ2ОБР(α;степеней свободы)
| Число степеней свободы k | Уровень значимости a | |||||
| 0,01 | 0,025 | 0.05 | 0,95 | 0,975 | 0.99 | |
| 1 | 6.6 | 5.0 | 3.8 | 0.0039 | 0.00098 | 0.00016 |
| 2 | 9.2 | 7.4 | 6.0 | 0.103 | 0.051 | 0.020 |
| 3 | 11.3 | 9.4 | 7.8 | 0.352 | 0.216 | 0.115 |
| 4 | 13.3 | 11.1 | 9.5 | 0.711 | 0.484 | 0.297 |
| 5 | 15.1 | 12.8 | 11.1 | 1.15 | 0.831 | 0.554 |
| 6 | 16.8 | 14.4 | 12.6 | 1.64 | 1.24 | 0.872 |
| 7 | 18.5 | 16.0 | 14.1 | 2.17 | 1.69 | 1.24 |
| 8 | 20.1 | 17.5 | 15.5 | 2.73 | 2.18 | 1.65 |
| 9 | 21.7 | 19.0 | 16.9 | 3.33 | 2.70 | 2.09 |
| 10 | 23.2 | 20.5 | 18.3 | 3.94 | 3.25 | 2.56 |
| 11 | 24.7 | 21.9 | 19.7 | 4.57 | 3.82 | 3.05 |
| 12 | 26.2 | 23.3 | 21 .0 | 5.23 | 4.40 | 3.57 |
| 13 | 27.7 | 24.7 | 22.4 | 5.89 | 5.01 | 4.11 |
| 14 | 29.1 | 26.1 | 23.7 | 6.57 | 5.63 | 4.66 |
| 15 | 30.6 | 27.5 | 25.0 | 7.26 | 6.26 | 5.23 |
| 16 | 32.0 | 28.8 | 26.3 | 7.96 | 6.91 | 5.81 |
| 17 | 33.4 | 30.2 | 27.6 | 8.67 | 7.56 | 6.41 |
| 18 | 34.8 | 31.5 | 28.9 | 9.39 | 8.23 | 7.01 |
| 19 | 36.2 | 32.9 | 30.1 | 10.1 | 8.91 | 7.63 |
| 20 | 37.6 | 34.2 | 31.4 | 10.9 | 9.59 | 8.26 |
| 21 | 38.9 | 35.5 | 32.7 | 11.6 | 10.3 | 8.90 |
| 22 | 40.3 | 36.8 | 33.9 | 12.3 | 11.0 | 9.54 |
| 23 | 41.6 | 38.1 | 35.2 | 13.1 | 11.7 | 10.2 |
| 24 | 43.0 | 39.4 | 36.4 | 13.8 | 12.4 | 10.9 |
| 25 | 44.3 | 40.6 | 37.7 | 14.6 | 13.1 | 11.5 |
| 26 | 45.6 | 41.9 | 38.9 | 15.4 | 13.8 | 12.2 |
| 27 | 47.0 | 43.2 | 40.1 | 16.2 | 14.6 | 12.9 |
| 28 | 48.3 | 44.5 | 41.3 | 16.9 | 15.3 | 13.6 |
| 29 | 49.6 | 45.7 | 42.6 | 17.7 | 16.0 | 14.3 |
| 30 | 50.9 | 47.0 | 43.8 | 18.5 | 16.8 | 15.0 |