Вычисление определителей методом Гаусса
Применим метод Гаусса для вычисления определителя ∆. При решении системы уравнений:Ax = b
методом Гаусса мы путём преобразования по схеме единственного деления привели её к треугольному виду:
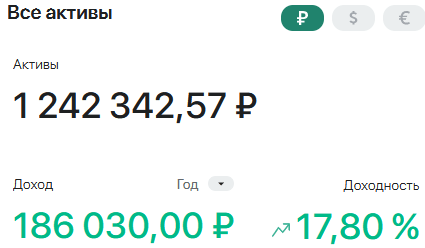
B x = β
где 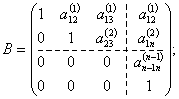
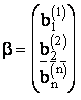
Определитель detB = 1.
Элементы матрицы B получились из матрицы A с помощью следующих элементарных преобразований:
1) деления на ведущие элементы a11 матрицы A ,
2) вычитания из строк матрицы A и промежуточных матриц Ai, i=1,n-1 чисел, пропорциональных элементам соответствующих ведущих строк.
При первой операции определитель матрицы также делится на соответствующий ведущий элемент, т.е.
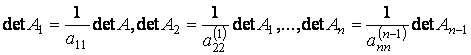
Следовательно:
При второй операции определитель не изменится.
Перейти к онлайн решению своей задачи
Пример. Данную матрицу свести к треугольной и найти определитель.
| 2 | 6 | 5 | 3 | 2 |
| -1 | 3 | 0 | 1 | -2 |
| 6 | 5 | 4 | 0 | 2 |
| 0 | 1 | 5 | 3 | -2 |
| 5 | 3 | 0 | 1 | 0 |
Добавим 5-ую строку к 4-ой:
| 2 | 6 | 5 | 3 | 2 |
| -1 | 3 | 0 | 1 | -2 |
| 6 | 5 | 4 | 0 | 2 |
| 5 | 4 | 5 | 4 | -2 |
| 5 | 3 | 0 | 1 | 0 |
| 2 | 6 | 5 | 3 | 2 |
| -1 | 3 | 0 | 1 | -2 |
| 6 | 5 | 4 | 0 | 2 |
| 5 | 4 | 5 | 4 | -2 |
| 0 | -1 | -5 | -3 | 2 |
| 2 | 6 | 5 | 3 | 2 |
| -1 | 3 | 0 | 1 | -2 |
| 6 | 5 | 4 | 0 | 2 |
| 0 | -1/6 | 5/3 | 4 | -11/3 |
| 0 | -1 | -5 | -3 | 2 |
| 2 | 6 | 5 | 3 | 2 |
| -1 | 3 | 0 | 1 | -2 |
| 0 | 23 | 4 | 6 | -10 |
| 0 | -1/6 | 5/3 | 4 | -11/3 |
| 0 | -1 | -5 | -3 | 2 |
| 2 | 6 | 5 | 3 | 2 |
| 0 | 6 | 5/2 | 5/2 | -1 |
| 0 | 23 | 4 | 6 | -10 |
| 0 | -1/6 | 5/3 | 4 | -11/3 |
| 0 | -1 | -5 | -3 | 2 |
Умножим 4-ую строку на (k = -1 / 1/6 = -6) и добавим к 5-ой:
| 2 | 6 | 5 | 3 | 2 |
| 0 | 6 | 5/2 | 5/2 | -1 |
| 0 | 23 | 4 | 6 | -10 |
| 0 | -1/6 | 5/3 | 4 | -11/3 |
| 0 | 0 | -15 | -27 | 24 |
| 2 | 6 | 5 | 3 | 2 |
| 0 | 6 | 5/2 | 5/2 | -1 |
| 0 | 23 | 4 | 6 | -10 |
| 0 | 0 | 39/23 | 93/23 | -86/23 |
| 0 | 0 | -15 | -27 | 24 |
| 2 | 6 | 5 | 3 | 2 |
| 0 | 6 | 5/2 | 5/2 | -1 |
| 0 | 0 | -67/12 | -43/12 | -37/6 |
| 0 | 0 | 39/23 | 93/23 | -86/23 |
| 0 | 0 | -15 | -27 | 24 |
Умножим 4-ую строку на (k = 15 / 39/23 = 115/13) и добавим к 5-ой:
| 2 | 6 | 5 | 3 | 2 |
| 0 | 6 | 5/2 | 5/2 | -1 |
| 0 | 0 | -67/12 | -43/12 | -37/6 |
| 0 | 0 | 39/23 | 93/23 | -86/23 |
| 0 | 0 | 0 | 114/13 | -118/13 |
| 2 | 6 | 5 | 3 | 2 |
| 0 | 6 | 5/2 | 5/2 | -1 |
| 0 | 0 | -67/12 | -43/12 | -37/6 |
| 0 | 0 | 0 | 198/67 | -376/67 |
| 0 | 0 | 0 | 114/13 | -118/13 |
Умножим 4-ую строку на (k = -114/13 / 198/67 = -1273/429) и добавим к 5-ой:
| 2 | 6 | 5 | 3 | 2 |
| 0 | 6 | 5/2 | 5/2 | -1 |
| 0 | 0 | -67/12 | -43/12 | -37/6 |
| 0 | 0 | 0 | 198/67 | -376/67 |
| 0 | 0 | 0 | 0 | 250/33 |
Ранг матрицы равен r=5
Определитель матрицы ∆ = 2 • 6 • (-67/12) • 198/67 • 250/33 = -1500