Биссектриса угла треугольника
Задание. Даны координаты треугольника: A(2,1), B(1,-2), C(-1,0).Решение получаем с помощью сервиса
Координаты треугольника. 1) Координаты векторов
Координаты векторов находим по формуле:
X = xj-xi; Y = yj-yi
здесь X,Y координаты вектора; xi, yi-координаты точки Аi; xj, yj-координаты точки Аj
Например, для вектора AB
X = x2-x1; Y = y2-y1
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Длина сторон треугольника
Длина вектора a(X;Y) выражается через его координаты формулой:
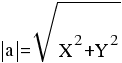
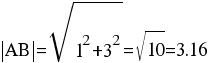
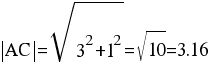
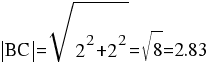
3) Угол между прямыми
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле:
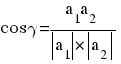
где a1a2 = X1X2+Y1Y2
Найдем угол между сторонами AB и AC
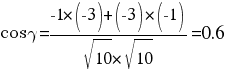
γ = arccos(0.6) = 53.130
8) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
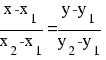
Уравнение прямой AB
Каноническое уравнение прямой:
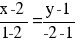 или
или 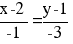
или
y = 3x -5 или y -3x +5 = 0
Уравнение прямой AC
Каноническое уравнение прямой:
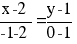 или
или 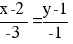
или
y = 1/3x+1/3 или 3y -x-1 = 0
Уравнение прямой BC
Каноническое уравнение прямой:
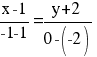
или
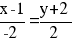
или
y = -x -1 или y+x +1 = 0
Нахождение биссектрисы угла из свойств углов треугольника
Найдем биссектрису угла A. Точку пересечения биссектрисы со стороной BC обозначим М.Воспользуемся формулой:
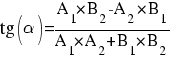
Уравнение AB: y -3x +5 = 0, уравнение AC: 3y -x-1 = 0
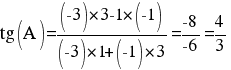
∠A ≈ 53.130
Биссектриса делит угол пополам, следовательно угол NAK ≈ 270
Тангенс угла наклона AB равен 3/1 (т.к. y = 3x -5). Угол наклона равен 71.570
∠NKA≈ 1800-71.570 = 108.430
∠ANK ≈ 1800-(108.430+26.570) ≈ 450
tg(450) = 1
Биссектриса проходит через точку A(2,1), используя формулу, имеем:
y-y0 = k(x-x0)
y-1 = 1(x-2) или y=x-1
Нахождение биссектрисы угла из свойств векторов
Найдем биссектрису угла A.
Известно, что диагонали ромба делят углы пополам. Найдем орты векторов AC(-1,-3) и AB(-3,-1). Соответственно и на них, как на сторонах, построим ромб, диагональ которого AK, равную сумме ортов, можно взять в качестве направляющего вектора биссектрисы.
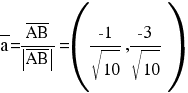
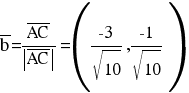
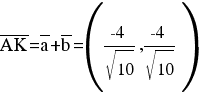
Каноническое уравнение биссектрисы AK примет вид:
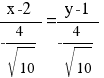 или
или 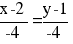
y=x-1 или y-x+1=0
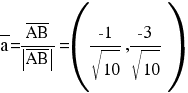
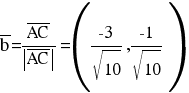
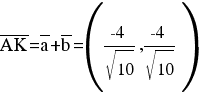
Каноническое уравнение биссектрисы AK примет вид:
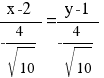 или
или 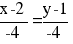
y=x-1 или y-x+1=0