Гипербола

Гипербола - геометрическое место точек, для каждой из которых модуль разности расстояний от нее до двух данных точек F₁,F₂ (фокусы) есть величина постоянная, равная 2a.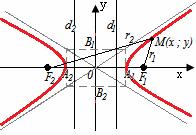

Элементы гиперболы:
A₁A₂=2a - действительная ось
B₁B₂=2b - мнимая ось
A₁,A₂ - вершины
F₁(c ; 0), F₂(-c ; 0) - фокусы
F₁F₂=2c - фокальное расстояние (фокусное расстояние)

c²=a²+b²

- асимптоты

- эксцентриситет (c > a). Его можно рассматривать, как числовую характеристику величины раствора угла между асимптотами.
r₁=±(εx-a), r₁=±(εx+a), - фокальные радиусы (верхний знак соответствует правой, нижний – левой ветви)

- директрисы

Геометрический смысл мнимой оси показан на рисунке пунктирной линией (расстояние между асимптотами).
Каноническое уравнение гиперболы (координатные оси совпадают с осями гиперболы):

Параметрические уравнения:

График гиперболы

Пример ввода:y^2-9*x^2-126*y+36*x+32, y^2/2-x^2-x*y+3*x+2

Свойства равносторонней гиперболы

Мнимая ось 2b может быть больше, меньше или равна действительной оси 2a. Если действительная и мнимая оси равны (a=b), то гипербола называется равносторонней (или равнобочной). Эксцентриситет равносторонней гиперболы равен sqrt(2).
Асимптоты равносторонней гиперболы взаимно перпендикулярны.

Сопряженные гиперболы

Две гиперболы называются сопряженными, если они имеют общий центр и общие оси, но действительная ось одной из них является мнимой осью другой. Сопряженные гиперболы имеют общие асимптоты.
Уравнение гиперболы, сопряженной данной: