Уравнение высоты треугольника и ее длина
Пример. Даны вершины треугольника АВС.Найти: 1) длину стороны АВ; 2) уравнения сторон АВ и АС и их угловые коэффициенты; 3) Внутренний угол А в радианах с точностью до 0,01; 4) уравнение высоты CD и ее длину; 5) уравнение окружности, для которой высота CD есть диаметр; 6) систему линейных неравенств, определяющих треугольник АВС.
|AB| = 15
|AC| = 11.18
|BC| = 14.14
Расстояние d от точки M: d = 10
Даны координаты вершин треугольника: A(-5,2), B(7,-7), C(5,7).
2) Длина сторон треугольника
Расстояние d между точками M1(x1; y1) и M2(x2; y2) определяется по формуле:
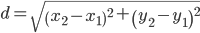
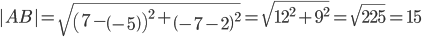
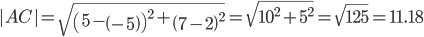
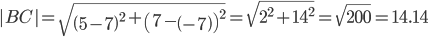
8) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:

Уравнение прямой AB
Каноническое уравнение прямой:
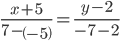 или
или 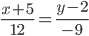
или y = -3/4x -7/4 или 4y + 3x +7 = 0
Уравнение прямой AC
Каноническое уравнение прямой:
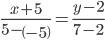 или
или 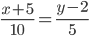
или y = 1/2x + 9/2 или 2y -x - 9 = 0
Уравнение прямой BC
Каноническое уравнение прямой:
 или
или 
или y = -7x + 42 или y + 7x - 42 = 0
3) Угол между прямыми
Уравнение прямой AB:y = -3/4x -7/4
Уравнение прямой AC:y = 1/2x + 9/2
Угол φ между двумя прямыми, заданными уравнениями с угловыми коэффициентами y = k1x + b1 и y2 = k2x + b2, вычисляется по формуле:

Угловые коэффициенты данных прямых равны -3/4 и 1/2. Воспользуемся формулой, причем ее правую часть берем по модулю:
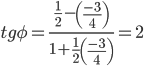
tg φ = 2
φ = arctg(2) = 63.440 или 1.107 рад.
9) Уравнение высоты через вершину C
Прямая, проходящая через точку N0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
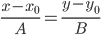
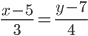
y = 4/3x + 1/3 или 3y -4x - 1 = 0
Данное уравнение можно найти и другим способом. Для этого найдем угловой коэффициент k1 прямой AB.
Уравнение AB: y = -3/4x -7/4, т.е. k1 = -3/4
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим :
-3/4k = -1, откуда k = 4/3
Так как перпендикуляр проходит через точку C(5,7) и имеет k = 4/3,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = 5, k = 4/3, y0 = 7 получим:
y-7 = 4/3(x-5)
или
y = 4/3x + 1/3 или 3y -4x - 1 = 0
Найдем точку пересечения с прямой AB:
Имеем систему из двух уравнений:
4y + 3x +7 = 0
3y -4x - 1 = 0
Из первого уравнения выражаем y и подставим во второе уравнение.
Получаем: x = -1; y = -1
D(-1;-1)
9) Длина высоты треугольника, проведенной из вершины C
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:
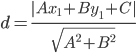
Найдем расстояние между точкой C(5;7) и прямой AB (4y + 3x +7 = 0)
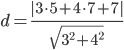
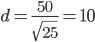
Длину высоты можно вычислить и по другой формуле, как расстояние между точкой C(5;7) и точкой D(-1;-1).
Расстояние между двумя точками выражается через координаты формулой:
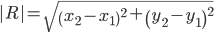
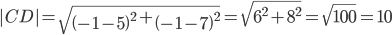
5) уравнение окружности, для которой высота CD есть диаметр;
Уравнение окружности радиуса R с центром в точке E(a;b) имеет вид:
(x-a)2 + (y-b)2 = R2
Так как CD является диаметром искомой окружности, то ее центр Е есть середина отрезка CD. Воспользовавшись формулами деления отрезка пополам, получим:
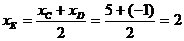
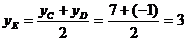
Следовательно, Е(2;3) и R = CD / 2 = 5. Использую формулу, получаем уравнение искомой окружности: (x-2)2 + (y-3)2 = 25
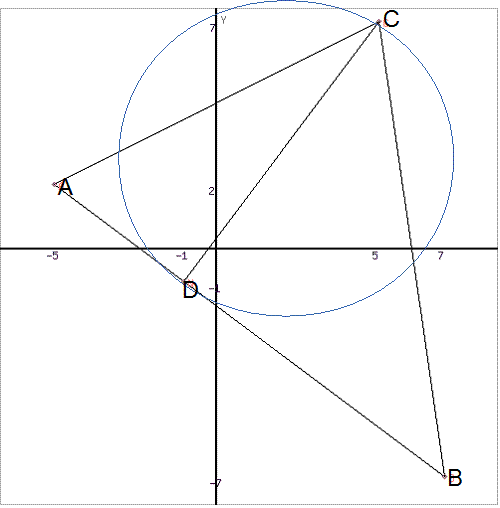
6) система линейных неравенств, определяющих треугольник АВС.
Уравнение прямой AB: y = -3/4x -7/4
Уравнение прямой AC : y = 1/2x + 9/2
Уравнение прямой BC : y = -7x + 42
Система линейных неравенств:
y ≥ -3/4x -7/4 или y + 3/4x ≥ -7/4 или 3x + 4y ≥ -7
y ≤ 1/2x + 9/2 или y - 1/2x ≤ 9/2 или - x + 2y ≤ 9
y ≤ -7x + 42 или y + 7x ≤ 42 или 7x + y ≤ 42