Объем тетраэдра
Пример №1. Найти объем треугольной пирамиды ABCD с вершинами A(2;-1;1), B(5;5;4), C(3;2;-1), D(4;1;3).Решение находим с помощью калькулятора.
Найти объем треугольной пирамиды ABCD с вершинами A(2;-1;1), B(5;5;4), C(3;2;-1), D(4;1;3).
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
здесь X,Y,Z координаты вектора; xi, yi, zi - координаты точки Аi; xj, yj, zj - координаты точки Аj;
Например, для вектора AB
X = x2 - x1; Y = y2 - y1; Z = z2 - z1
X = 5-2; Y = 5-(-1); Z = 4-1
AB(3;6;3), AC(1;3;-2), AD(2;2;2), BC(-2;-3;-5), BD(-1;-4;-1), CD(1;-1;4).
Объем пирамиды, построенный на векторах a1(X1;Y1;Z1), a2(X2;Y2;Z2), a3(X3;Y3;Z3) равен:
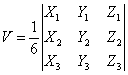
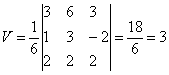
Находим определитель матрицы: ∆ = 3 • (3 • 2-2 • (-2))-1 • (6 • 2-2 • 3)+2 • (6 • (-2)-3 • 3) = -18
Пример №2. Вычислить объем тетраэдра с вершинами в точках A, B, C, D: A(14;4;5), B(–5;–3;2), C(–2;–6;–3), D(–2;2;–1).
Решение.
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi; Z = zj - zi
AB(-19;-7;-3), AC(-16;-10;-8), AD(-16;-2;-6), BC(3;-3;-5), BD(3;5;-3), CD(0;8;2).
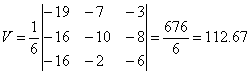
Определитель матрицы находим по формуле:
∆ = (-19) • ((-10) • (-6)-(-2) • (-8))-(-16) • ((-7) • (-6)-(-2) • (-3))+(-16) • ((-7) • (-8)-(-10) • (-3)) = -676

