Векторное произведение
Инструкция. Заполните координаты векторов и нажмите кнопку Решение.
Например, для вектора
a = 2i - 2j + k необходимо ввести: 2;-2;1
Свойства векторного произведения
Векторным произведением двух векторов a и b называется третий вектор c, удовлетворяющий условиям:1) модуль вектора c равен произведению модулей векторов a и b на синус угла между ними, т.е.:
3) вектор c направлен так, что кратчайший поворот вектора a к вектору b виден из конца вектора c происходящим против часовой стрелки (т.е. векторы a, b и c) образуют правую упорядоченную тройку, или правый репер).
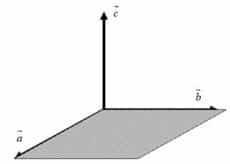
Модуль векторного произведения равен площади параллелограмма S, построенного на векторах a и b.
Векторное произведение выражается формулой:
Векторное произведение векторов a(x1;y1;z1) и b(x2;y2;z2), заданных своими координатами, вычисляется следующим образом:
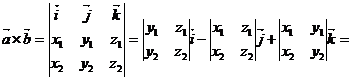
(y1z2-z1y2)i - (z1x2-x1z2)j + (x1y2-y1x2)k
Физический смысл векторного произведения состоит в следующем. Если F - сила, а r - радиус-вектор точки е приложения, имеющий начало в точке О, то момент силы F относительно точки О есть вектор, равный векторному произведению r на F, т.е. m0(F)=r × F.
Свойства векторного произведения орт правой системы координат:
- i × j=k
- j × k=i
- k × i=j
- j × i=-k
- k × j=-i
- i × k=-j
Найти векторное произведение векторов и синус угла между ними, если А{-2; 2; -2}, B{4; -4; 4}.

