Анализ эффективности оптимального решения задачи графическим методом
Предприятие выпускает два вида продукции (A и B), используя при этом три вида ресурсов. Известны объемы каждого вида ресурсов (bi, i=1,2,3), доход от реализации единицы продукции каждого вида (cj, j=1,2), а также нормы расхода ресурсов на изготовление единицы продукции каждого вида (aij, i=1,2,3, j=1,2). Определить план выпуска продукции, максимизирующий суммарный доход.- Построить математическую модель указанной ниже задачи о распределении ресурсов в виде задачи линейного программирования (ЛП).
- Используя графические методы, исследовать полученную модель на устойчивость к изменениям правой части (по каждому ресурсу отдельно) и целевой функции.
1. Геометрический метод позволил получить статическую область допустимых решений, представленную на рис. 1.7. Рассмотрим, как влияет на оптимальное решение изменение запасов ресурсов А и В и соотношения в производстве красок.
2. Оптимальное решение задачи получено в точке Е. Эта точка образована пересечением прямых, соответствующих ресурсам (1) и (2). Следовательно, ресурсы (1) и (2) - дефицитные ресурсы, а ресурсы (3) - (6) - недефицитные, так как они имеются в избытке.
3. Для дефицитных ресурсов определим предельно допустимое увеличение запасов, позволяющее улучшить найденное оптимальное решение.
4. В рассматриваемой задаче используемые запасы сырья А и В являются дефицитными ресурсами (1) и (2), поэтому последовательно рассмотрим сначала увеличение запасов сырья А (ресурса 1). На рис. 1.10 видно, что при увеличении запаса этого ресурса прямая (1) перемещается вверх параллельно самой себе.
При этом треугольник DKE стягивается в точку К. В этом случае, областью допустимых решений становится многоугольник ABCKF, а оптимальному решению соответствует точка К. Ограничения (2) и (4) становятся связующими. В точке К ограничение (1) становится избыточным, поскольку любое дальнейшее увеличение запаса ресурса А не влияет ни на область допустимых решений, ни на оптимальное решение.
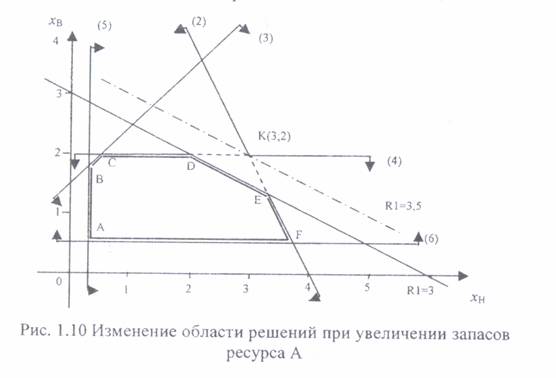
5. Для определения координат точки К решим систему уравнений (2) и (4)
xн +0,5xв = 4
xв = 2
Решение этой системы : xв = 2 и xн = 3, т.е. К(3;2).
6. Подстановка координат точки К(3; 2) в левую часть ограничения (1) определяется максимально допустимый запас ресурса А: R1(K) = 0,5xн + хв= 0,5·3 + 2 = 3,5 (т)
7. Определим предельное увеличение запаса ресурса А: ΔR1 = R1(K) – R1 исходное = 3,5 - 3 = 0,5 (т)
8. Новое оптимальное значение целевой функции будет равно: Fmax(K) = 2·3 + 3·2=12 (тыс. руб.).
9. Увеличение функции цели составит: ΔF(K) = Fmax(K) - Fmax исходное =
10. Коэффициент эффективности сырья А (ресурса 1) составит Е1 = ΔF(K)/ΔR1=
.
11. Аналогично решается задача о целесообразности увеличения запасов дефицитного ресурса (2) (сырья В) в соответствующем ограничении (2) (рис. 1.11).
12. Новым оптимальным решением слановится точка L, где пересекаются прямые (1) и (6), т. е. 0,5xн + xв = 3 и xв = 0,5. Очевидно, ее координаты xн = 5 и xв = 0,5, причем запас сырья В можно увеличить до значения, равного ΔR2 = R2(L) - R2 исходное = (xн+ 0,5xв) - R2 = (5 +0,5·0,5) - 4 = 5,25 - 4 = 1,25 (т), т. е. на 1,25 т,
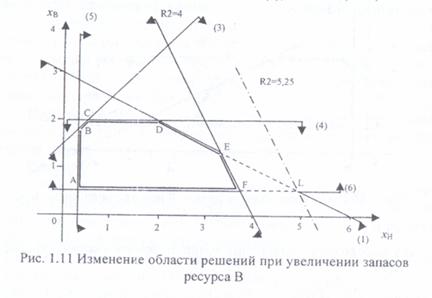
13. Новое оптимальное значение целевой функции в точке L будет равно: Fmax(L) = 2 · 5 + 3 · 0,5 = 11,5 (тыс. руб.). Увеличение функ ции цели составит: ΔF(L) = Fmax(L) – Fmaxисходное=
14. Коэффициент эффективности сырья В (ресурса 2) составит
На основе полученных данных можно сделать вывод о том, что дополнительные вложения (инвестиции) следует направить прежде всего на увеличение ресурса (1) (сырье А)
, а затем – ресурса (2) 
.
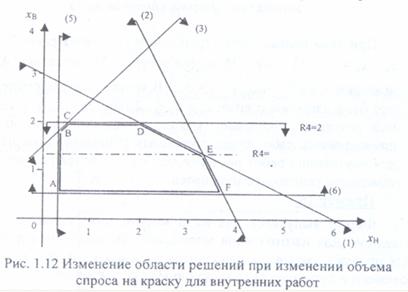
15. Для недефицитных ресурсов определим излишки недефицитных ресурсов (возможность снижения запасов недефицитных ресурсов, т. е. решим задачу об уменьшении правой части несвязанных ограничений).
Ограничение (4) xв ≤ 2 задает уровень спроса на краску для внутренних работ. На рис. 1.12 видно, что прямую CD (4) можно опускать параллельно вниз до точки оптимума Е с координатами (
; 
), не изменяя оптимального решения. Таким образом, при уменьшении спроса на краску для внутренних работ до величины 
оптимальность полученного ранее решения сохраняется. Излишки ресурса (4) составляют ΔR4 = R4 исходное – 
. Следовательно, предприятие может сохранять найденный оптимальный план (
) при уменьшении спроса на краску для внутренних работ до тонны.
Ограничение (3): хв - хн ≤ 1,5 представляет соотношение между суточным спросом на краску для внутренних работ и суточным спросом на краску для наружных работ. В этом случае, правую часть ограничения также можно уменьшать до тех пор, пока прямая ВС (3) (рис. 1.13) не достигнет точки Е.
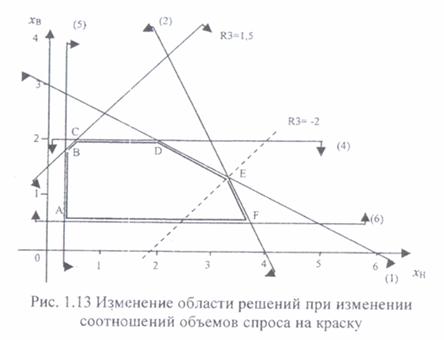
При этом правая часть ограничения (3) станет равной:
. Излишки ресурса (3) составляют ΔR3 = R3
исходное - R3(E) = 1,5 -(-2) = 3,5. В точке Е соотношение (3) может быть записано в виде: xв - хн ≤ -2 или хн - xв ≥ 2. Полученный результат показывает, что если суточный спрос на краску для наружных работ будет превышать суточный спрос на краску для внутренних работ не менее чем на 2 т, ранее полученное оптимальное решение не измениться.