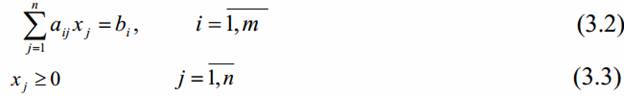Метод ветвей и границ
Метод ветвей и границ относится к группе комбинаторных методов дискретного программирования и является одним из наиболее распространенных методов этой группы. Центральную идею комбинаторных методов составляет замена полного перебора допустимого множества X частичным перебором. В случае метода ветвей и границ это осуществляется путем последовательного разбиения допустимого множества на подмножества (ветвления) и вычисления оценок (границ), позволяющих отбрасывать подмножества, заведомо не содержащие решения задачи.
При реализации общей схемы метода ветвей и границ для различных задач дискретного программирования необходимо, исходя из специфики этих задач, конкретизировать правила ветвления и вычисления границ.
Метод ветвей и границ решения целочисленных задач линейного программирования (ЦЗЛП)
Наиболее известным комбинаторным методом является метод ветвей и границ, который также опирается на процедуру решения задачи с ослабленными ограничениями. При таком подходе из рассматриваемой задачи получаются две подзадачи путем специального «разбиения» пространства решений и отбрасывания областей, не содержащих допустимых целочисленных решений.
В случае когда целочисленные переменные являются булевыми, применяются комбинированные методы. Булевы свойства переменных существенно упрощают поиск решения.
Рассматриваемый в данном разделе метод ветвей и границ решения задачи целочисленного программирования также опирается на решение задачи с ослабленными ограничениями. Метод ветвей и границ непосредственно применим как к полностью, так и к частично целочисленным задачам.
Согласно общей идее метода, сначала решается задача с ослабленными ограничениями (задача линейного программирования). Пусть хr — целочисленная переменная, значение xr* которой в оптимальном решении ослабленной задачи является дробным. Интервал [xr*] < xr < [xr*] +1 не содержит допустимых целочисленных компонент решения. Поэтому допустимое целое значение хr должно удовлетворять одному из неравенств xr ≤[ xr* ] или хr ≥[ xr* ] +1.
Введение этих условий в задачу с ослабленными ограничениями порождает две не связанные между собой задачи. В таком случае говорят, что исходная задача разветвляется (или разбивается) на две подзадачи. Осуществляемый в процессе ветвления учет необходимых условий целочисленности позволяет исключить части многогранника допустимых решений, не содержащие точек с целыми координатами.
Затем каждая подзадача решается как задача линейного программирования (с целевой функцией исходной задачи). Если полученный оптимум оказывается допустимым для целочисленной задачи, такое решение следует зафиксировать как наилучшее. При этом нет необходимости продолжать«ветвление» подзадачи, поскольку улучшить полученное решение, очевидно, не удастся. В противном случае подзадача, в свою очередь, должна быть разбита на две подзадачи опять при учете условия целочисленности переменных, значения которых в оптимальном решении не являются целыми. Разумеется, как только полученное допустимое целочисленное решение одной из подзадач оказывается лучше имеющегося, оно фиксируется вместо зафиксированного ранее. Процесс ветвления продолжается, насколько это возможно, до тех пор, пока каждая подзадача не приведет к целочисленному решению или пока не будет установлена невозможность улучшения имеющегося решения. В этом случае зафиксированное допустимое решение является оптимальным. Эффективность вычислительной схемы метода можно повысить, введя в рассмотрение понятие границы, на основе которого делается вывод о необходимости дальнейшего разбиения каждой из подзадач.
Если оптимальное решение подзадачи с ослабленными ограничениями обеспечивает худшее значение целевой функции, чем имеющееся решение, эту подзадачу далее рассматривать не следует. В таких случаях говорят, что подзадача прозондирована, и ее можно вычеркнуть из списка подзадач, порожденных исходной задачей. Иными словами, как только получено допустимое целочисленное решение некоторой подзадачи, целочисленное решение некоторой подзадачи, соответствующее значение целевой функции может быть использовано в качестве(верхней в случае минимизации и нижней в случае максимизации) границы, наличие которой позволяет формализовать процедуру исключения прозондированных подзадач.
Рассмотрим задачу целочисленного линейного программирования (ЗЦЛП) :
Найти вектор 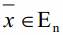 , максимизирующий линейную форму
, максимизирующий линейную форму 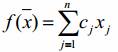 (3.1)
(3.1)
и удовлетворяющий условиям:
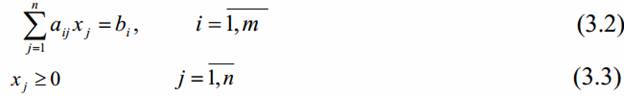
x1, x2,…,xp –целые (p≤n) (3.4)
Пусть, для каждой целочисленной переменной можно указать верхнюю и нижнюю границы, в пределах которых безусловно содержатся ее оптимальные значения, то есть
Vj ≤xj≤ Wj, (3.5)
При этом в систему функциональных ограничений необходимо включить р неравенств (3.5).
В начале любой S-й итерации метода ветвей и границ необходимо иметь:
1. Основной список задач линейного программирования, каждая из которых должна быть решена в последующих итерациях (на первой итерации список содержит одну ЗЛП- задачу 1 (3.1- 3.3) и (3.5).
2. Нижнюю границу оптимального значения линейной формы задачи (3.1) - (3.3), (3.5) Z0(s). На первой итерации в качестве Z0(1) можно взять значение функции f(x) в любой целочисленной точке x, лежащей внутри области(3.2) - (3.5). Если такую точку указать трудно, то можно положить Z0(1) = - ∞, но это приводит к значительному увеличению числа итераций.
Первоначально находим симплексным методом или методом искусственного базиса оптимальный план задачи без учета целочисленности переменных. Если среди компонент этого плана нет дробных чисел, то тем самым найдено искомое решение данной задачи.
Если среди компонент плана имеются дробные числа, то необходимо осуществить переход к новым планам, пока не будет найдено решение задачи.
Метод ветвей и границ основан на предположении, что новый оптимальный нецелочисленный план дает значение функции, большее, чем всякий последующий план перехода
Пусть переменная xi в плане дробное число. Тогда в оптимальном план ее значение будет , по крайней мере:
- либо меньше или равно ближайшему меньшему целому числу Ki*.
- либо больше или равно ближайшему большему целому числу Ki*.
Определяя эти числа симплексным методом решения двух задач линейного программирования:
1) F=∑cjxj → max
∑aijxj ≤ bi
xi ≤Ki*
xj≥0, xj – целые, j=1..n
2) F=∑cjxj → max
∑aijxj ≤ bi
xi ≥Ki*+1
xj≥0, xj – целые, j=1..n
Возможны четыре случая при решении этой пары задач:
1) Одна из задач неразрешима, а другая имеет целочисленный оптимальный план. Тогда этот план и значение целевой функции и дают решение исходной задачи.
2) Одна из задач неразрешима, а другая имеет нецелочисленный оптимальный план. Тогда рассматривается вторая задача и в ее оптимальном плане выбирается одна из компонент, значение которой равно дробному числу и строятся две новые задача, аналогично предыдущим.
3) Обе задачи разрешимы. Одна из задач имеет оптимальный целочисленный план, а в оптимальном плане другой задачи есть дробные числа. Тогда вычисляем значение целевой функции от планов и сравниваем их между собой. Если на целочисленном оптимальном план значение целевой функции больше или равно ее значению в плане, среди компонент которого есть дробные числа, то данный целочисленный план является оптимальным для исходной задачи и дает искомое решение.
4) Обе задачи разрешимы, и среди оптимальных планов обеих задач есть дробные числа. Тогда рассматриваем ту из задач, для которой значение целевой функции является наибольшим. Строятся новые две задачи.
Алгоритм метода ветвей и границ
- Находится решение задачи линейного программирования без учета целочисленности
- Составляется дополнительные ограничения на дробную компоненту плана.
- Находится решение двух задач с ограничениями на компоненту.
- Строятся в случае необходимости дополнительные ограничения, согласно возможным четырем случаям. Определяется оптимальный целочисленный план, либо устанавливается неразрешимость задачи.
Для решения задачи целочисленного программирования методом ветвей и границ используется сервис Метод ветвей и границ.
Пример. Необходимо найти максимальное значение целевой функции F = 4x1+3x2→ max, при системе ограничений:
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1≥0 | (3) |
| x2≥0 | (4) |
где x1, x1- целые числа. Для решения используем сервис Метод ветвей и границ. Обозначим границы области многоугольника решений. Область допустимых решений представляет собой многоугольник. Прямая F(x) = constпересекает область в точке C. Так как точка C получена в результате пересечения прямых (1)и (2), то ее координаты удовлетворяют уравнениям этих прямых: 3x1+2x2≤16 2x1+3x2≤18 Решив систему уравнений, получим: x1= 2.4, x2= 4.4 Откуда найдем максимальное значение целевой функции: F(X) = 4*2.4 + 3*4.4 = 22.8 Оптимальное значение переменной x1=2.4 оказалось нецелочисленным.
Разбиваем задачу 1 на две подзадачи 11 и 12. В первой из них к условиям задачи 11 добавляется условие х1≥ 3, а к задаче 12 — условие х1≤ 2. Эта процедура называется ветвлениемпо переменной х1.
Решим графически задачу 11 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1≥3 | (3) |
| x1≥0 | (4) |
| x2≥0 | (5) |
Область допустимых решений представляет собой треугольник.
Решим графически задачу 12 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1≤2 | (3) |
| x1≥0 | (4) |
| x2≥0 | (5) |
Область допустимых решений представляет собой многоугольник. Оптимальное значение переменной x2=3.5 оказалось нецелочисленным. Разбиваем задачу 11 на две подзадачи 111 и 112. В первой из них к условиям задачи 111 добавляется условие х2≥ 4, а к задаче 112 — условие х2≤ 3. Решим графически задачу 111 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1≥3 | (3) |
| x2≥4 | (4) |
| x1≥0 | (5) |
| x2≥0 | (6) |
Задача не имеет допустимых решений. ОДР представляет собой пустое множество. Задача 111 не имеет решения, поэтому для нее процесс ветвления прерываем. Решим графически задачу 112 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1≥3 | (3) |
| x2≤3 | (4) |
| x1≥0 | (5) |
| x2≥0 | (6) |
Оптимальное значение переменной x1=3.33 оказалось нецелочисленным. Разбиваем задачу 112 на две подзадачи 1121 и 1122. В первой из них к условиям задачи 1121 добавляется условие х1≥ 4, а к задаче 1122 — условие х1≤ 3. Решим графически задачу 1121 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1≥3 | (3) |
| x2≤3 | (4) |
| x1≥4 | (5) |
| x1≥0 | (6) |
| x2≥0 | (7) |
Решение задачи получилось целочисленным. Новое значение текущего рекорда будет равно F(X) = 22. Так как найденная точка является первым целочисленным решением, то ее и соответствующее ей значение ЦФ следует запомнить. Сама точка называется текущим целочисленным рекордомили просто рекордом, а оптимальное значение целочисленной задачи — текущим значением рекорда. Это значение является нижней границей оптимального значения исходной задачи Z*. Решим графически задачу 1122 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1≥3 | (3) |
| x2≤3 | (4) |
| x1≤3 | (5) |
| x1≥0 | (6) |
| x2≥0 | (7) |
Сведем систему ограничений к следующему виду: | 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x1=3 | (3) |
| x2≤3 | (4) |
| x1≥0 | (5) |
| x2≥0 | (6) |
Область допустимых решений представляет собой одну точку.
Текущий рекорд Z=22≥21, поэтому прекращаем ветвление из этой вершины. Оптимальное значение переменной x2=4.4 оказалось нецелочисленным. Разбиваем задачу 1 на две подзадачи 11 и 12. В первой из них к условиям задачи 11 добавляется условие х2≥ 5, а к задаче 12 — условие х2≤ 4. Эта процедура называется ветвлениемпо переменной х2. Решим графически задачу 11 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≥5 | (3) |
| x1≥0 | (4) |
| x2≥0 | (5) |
Текущий рекорд Z=22≥21, поэтому прекращаем ветвление из этой вершины. Решим графически задачу 12 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1≥0 | (4) |
| x2≥0 | (5) |
Оптимальное значение переменной x1=2.67 оказалось нецелочисленным. Разбиваем задачу 12 на две подзадачи 121 и 122. В первой из них к условиям задачи 121 добавляется условие х1≥ 3, а к задаче 122 — условие х1≤ 2. Решим графически задачу 121 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1≥3 | (4) |
| x1≥0 | (5) |
| x2≥0 | (6) |
Решим графически задачу 122 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1≤2 | (4) |
| x1≥0 | (5) |
| x2≥0 | (6) |
Область допустимых решений представляет собой многоугольник Прямая F(x) = constпересекает область в точке D. Так как точка D получена в результате пересечения прямых (3)и (4), то ее координаты удовлетворяют уравнениям этих прямых: x2≤4 x1≤2 Решив систему уравнений, получим: x1= 2, x2= 4 Откуда найдем максимальное значение целевой функции: F(X) = 4*2 + 3*4 = 20
Текущий рекорд Z=22≥20, поэтому прекращаем ветвление из этой вершины Оптимальное значение переменной x2=3.5 оказалось нецелочисленным. Разбиваем задачу 121 на две подзадачи 1211 и 1212. В первой из них к условиям задачи 1211 добавляется условие х2≥ 4, а к задаче 1212 — условие х2≤ 3.
Решим графически задачу 1211 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1≥3 | (4) |
| x2≥4 | (5) |
| x1≥0 | (6) |
| x2≥0 | (7) |
Сведем систему ограничений к следующему виду: | 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2=4 | (3) |
| x1≥3 | (4) |
| x1≥0 | (5) |
| x2≥0 | (6) |
Задача не имеет допустимых решений. ОДР представляет собой пустое множество (рис. б). Задача 1211 не имеет решения, поэтому для нее процесс ветвления прерываем. Решим графически задачу 1212 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1≥3 | (4) |
| x2≤3 | (5) |
| x1≥0 | (6) |
| x2≥0 | (7) |
Оптимальное значение переменной x1=3.33 оказалось нецелочисленным. Разбиваем задачу 1212 на две подзадачи 12121 и 12122. В первой из них к условиям задачи 12121 добавляется условие х1≥ 4, а к задаче 12122 — условие х1≤ 3. Решим графически задачу 12121 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1≥3 | (4) |
| x2≤3 | (5) |
| x1≥4 | (6) |
| x1≥0 | (7) |
| x2≥0 | (8) |
Текущий рекорд Z=22≥22, поэтому прекращаем ветвление из этой вершины Решим графически задачу 12122 как задачу ЛП.
| 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1≥3 | (4) |
| x2≤3 | (5) |
| x1≤3 | (6) |
| x1≥0 | (7) |
| x2≥0 | (8) |
Сведем систему ограничений к следующему виду: | 3x1+2x2≤16 | (1) |
| 2x1+3x2≤18 | (2) |
| x2≤4 | (3) |
| x1=3 | (4) |
| x2≤3 | (5) |
| x1≥0 | (6) |
| x2≥0 | (7) |
Текущий рекорд Z=22≥21, поэтому прекращаем ветвление из этой вершины. F(X) = 22 x1= 4 x2= 2
Метод ветвей и границ для задачи коммивояжера
В задаче коммивояжера для формирования оптимального маршрута объезда n городов необходимо выбрать один лучший из (n-1)! вариантов по критерию времени, стоимости или длине маршрута. Эта задача связана с определением гамильтонова цикла минимальной длины. В таких случаях множество всех возможных решений следует представить в виде дерева - связного графа, не содержащего циклов и петель. Корень дерева объединяет все множество вариантов, а вершины дерева — это подмножества частично упорядоченных вариантов решений.
Вершина (i, j) соответствует подмножеству всех маршрутов, содержащих ребро (i,j), а вершина (i*,j*) — подмножеству всех маршрутов, где это ребро отсутствует.
Процесс разбиения на эти подмножества можно рассматривать как ветвление дерева. Поэтому метод называется методом поиска по дереву решений, или методом ветвей и границ.
Метод ветвей и границ представляет собой алгоритм направленного перебора множества вариантов решения задачи. Сущность метода ветвей и границ состоит в том, что от корня дерева ветвятся не все вершины.
![]() , максимизирующий линейную форму
, максимизирующий линейную форму 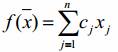 (3.1)
(3.1)