Задачи по экономико-математическому моделированию
Какие задачи стоят перед экономико-математическим моделированием? Моделирование является неотъемлемой составной частью экономической теории. Специфика математической экономики, ее методологическая особенность заключается в том, что она изучает не сами экономические объекты и явления как таковые, а их математические модели. Ее цель – получение объективной экономической информации и выработка имеющих важное практическое значение рекомендаций. Формально математическую экономику можно отнести как к экономической, так и к математической науке.Цель ЭММ – количественная оценка экономических процессов, протекающих в рамках исследуемой экономической системы
В первом случае ее следует понимать как раздел экономики, который изучает количественные и качественные категории, а также поведенческие аспекты экономических субъектов. Считая же математическую экономику одним из направлений математики, можно отнести ее к разделам прикладной математики, которые занимаются оптимизационными задачами и задачами принятия решения.
Моделирование сводится к тому, чтобы с помощью математических функций установить вид связи между эндогенными и экзогенными переменными системы:
Y = f(x1, x2,…,xk, a1,a2,…,an)
где: Y – эндогенная переменная; xi – экзогенные переменные; ai – параметры модели
Модель, в конечном счете, – некоторая функциональная связь между независимыми и зависимыми переменными
Основные математические модели и задачи
- Задачи математического программирования
- Модели конфликтных ситуаций в экономике
- Модели сетевого планирования и управления
- Модели системы массового обслуживания
- Модели сферы потребления
- Модели сферы производства
- Модели общего экономического равновесия
- Общие модели развития экономики
Задача № 1. Составить математические модели следующих задач:
Варианты 1 – 5. Кондитерский цех выпускает три вида конфет A,B,C, используя три вида сырья (какао, сахар, наполнитель). Нормы расхода сырья на производство 10 кг конфет а также прибыль от реализации 10 кг конфет каждого вида приведены в таблице:
| Сырье | Нормы расхода сырья | Запасы сырья | ||
| A | B | C | ||
| какао | a11 | a12 | a13 | b1 |
| сахар | a21 | a22 | a23 | b2 |
| наполнитель | a31 | a32 | a33 | b3 |
| прибыль | c1 | c2 | c3 | |
Составить план выпуска продукции, обеспечивающий максимум прибыли.
Перейти к онлайн решению своей задачи
Варианты 6 – 10. В рационе бройлерных цыплят птицеводческой фермы используется два вида кормов A и B. Цыплята должны получать три вида питательных веществ (известняк, зерно, соевые бобы). Содержание единиц питательных веществ в 1 кг каждого из видов корма приведено в таблице:
| Питательные вещества | Содержание питательного вещества в единице корма | Необходимое количество питательного вещества | |
| A | B | ||
| известняк | a11 | a12 | b1 |
| зерно | a21 | a22 | b2 |
| соевые бобы | a31 | a32 | b3 |
| стоимость единицы корма | c1 | c2 | |
Составить рацион кормления, обеспечивающий минимальные затраты.
Перейти к онлайн решению своей задачи
Задача № 2. Решить задачу линейного программирования графическим методом.
F(X)=c1x1+c2x2 → max(min)
c11x1+c12x2 ≤(≥) b1
c21x1+c22x2 ≤(≥) b2
c31x1+c32x2 ≤(≥) b3
x1 ≥ 0, x2 ≥ 0
Исходные данные записаны в таблице.
Перейти к онлайн решению этой задачи
Задача № 3. Решить симплексным методом задачу, математическая модель которой имеет следующий вид:
F(X) = c1 x1 + c2 x2 + c3 x3 → max (min)
a11x1 + a12x2 + a13x3 ≤ b1,
a21x1 + a22x2 + a23x3 ≤ b2,
a31x1 + a32x2 + a33x3 ≤ b3,
xi ≥ 0
Перейти к онлайн решению своей задачи
Задача № 4. Целевая функция ЗПР в условиях неопределенности задана таблицей
| В1 | В2 | В3 | В4 | |
| А1 | a11 | a12 | a13 | a14 |
| А2 | a21 | a22 | a23 | a24 |
| А3 | a31 | a32 | a33 | a34 |
| А4 | a41 | a42 | a43 | a44 |
Выбор, какой альтернативы здесь следует считать оптимальным? Решить четырьмя способами, применив критерии Лапласа, Вальда, Гурвица, Сэвиджа.
| 5 | 3 | 4 | 2 |
| 1 | 2 | 5 | 4 |
| 7 | 6 | 7 | 3 |
| 1 | 2 | 4 | 4 |
Решение. Задачу решаем с помощью данного сервиса. Выбираем размерность платежной матрицы 4x4. В разделе Вид критерия отмечаем: Лапласа, Вальда, Гурвица, Сэвиджа.
Скачать решение
Задача № 5.
Фирма может выпускать продукцию одного из шести видов: 1,2,3,4,5,6. Глава фирмы должен принять решение, какой из шести видов продукции выпускать в течение предстоящего летнего сезона. Предполагается, что вероятности дождливого, жаркого и умеренного лета (Д, Ж, У) равны соответственно - 0,2; 0,5; 0,3. Прибыль фирмы зависит от того, каким будет лето и определяется таблицей. Выбор, какого варианта производства будет оптимальным?
| Д | Ж | У | |
| 1 | 50 | 60 | 70 |
| 2 | 60 | 55 | 85 |
| 3 | 50 | 40 | 60 |
| 4 | 70 | 40 | 50 |
| 5 | 75 | 55 | 60 |
| 6 | 65 | 60 | 65 |
используем предыдущий сервис, только размерность матрицы будет 6x3, и заполняем соответствующие вероятности для критерия Байеса: 0.2; 0.5; 0.3.
Скачать решение
Задача № 6. Найдите решение следующей матричной игры
| 8 | 10 | 13 |
| 13 | 12 | 9 |
Задачу решаем с помощью данного сервиса. Задаем размерность платежной матрицы: 2x3. Метод решения: графический или симплекс-метод.
Скачать решение
Задача № 7. (Борьба за рынки сбыта)
Фирма А намерена сбыть партию товара на одном из двух рынков, которые контролируются более крупной фирмой В. С этой целью она проводит подготовительную работу, связанную с определенными затратами. Если фирма В разгадает, на каком рынке фирма А будет продавать свой товар, то она примет контрмеры и воспрепятствует “захвату” рынка (этот вариант означает поражение фирмы А); если нет, то фирма А одерживает победу. Предположим, что для фирмы А проникновение на первый рынок более выгодно, чем проникновение на второй, но и борьба за первый рынок требует от нее больших средств. Например, победа фирмы А на первом рынке приносит ей вдвое большую прибыль, чем победа на втором, но зато поражение на первом рынке полностью ее разоряет. Пусть для фирмы А ее победа на первом рынке оценивается в а21 ед., а на втором рынке – в a12 ед.; поражение фирмы А на первом рынке оценивается в a11 ед., а на втором – a22 ед. Для фирмы В ее победа составляет соответственно b11 и b22 ед., а поражение b12 и b21 ед. В результате получаем биматричную игру с матрицами выигрышей
Значения переменных по вариантам внесены в таблицу:
| –16 | 6 | 9 | –2 | |
| 3 | –2 | –1 | 4 |
Для решения применим сервис биматричная игра. Выбираем размерность платежной матрицы 2x2.
Скачать решение
Линейное программирование
Задача №1.Решить задачу ЛП геометрическим методом.
Дана целевая функция f = (x1,x2) и система ограничений. Найти максимум функции f(x1,x2)
Методические указания к решению задачи: для проверки решения задачи используйте сервис Решение задачи ЛП геометрическим методом.
Задание №2.
Решить задачу оптимального планирования выпуска продукции при следующих условиях.
Для изготовления двух видов продукции используются три вида сырья. При производстве единицы продукции первого вида затрачивается а1 кг сырья первого вида, а2 кг сырья второго вида и а3 кг сырья третьего вида. При производстве единицы продукции второго вида затрачивается в1 кг сырья первого вида, в2 кг сырья второго вида и в3 кг сырья третьего вида. Запасы сырья первого вида составляют А кг, второго - B кг, третьего - C кг. Прибыль от реализации единицы продукции первого вида составляет Р1 руб., от реализации единицы продукции второго вида - Р2 руб.
Конкретные исходные данные приведены в нижеследующей таблице.
Примечание: При оформлении решения должны быть выполнены все шаги алгоритма симплексного метода без пропусков промежуточных расчетов по аналогии с вышеприведенным примером.
Методические указания к решению задачи: для проверки решения задачи используйте сервис Алгоритм симплексного метода онлайн.
Задача 3.
Четыре предприятия данного экономического района для производства продукции используют три вида сырья. Спрос на сырье каждого из предприятий соответственно составляет В1, В2, В3, В4 и В5 усл. ед. Сырье сосредоточено в трех местах. Предложение поставщиков сырья равны: А1, А2 и А3. На каждое предприятие сырье может завозиться от любого поставщика. Тарифы известны и задаются матрицей. Требуется найти оптимальный план перевозок.
Методические указания к решению задачи: для проверки решения задачи используйте сервис Оптимальный план перевозок онлайн.
Задача №4.
На развитие трех предприятий выделено 5 млн. руб. Известна эффективность капитальных вложений в каждое предприятие, заданная значением нелинейной функции f(x) представленной в таблице. Необходимо распределить выделенные средства между предприятиями таким образом, чтобы получить максимальный суммарный доход.
Методические указания к решению задачи: для проверки решения задачи используйте сервис Распределение выделенных средств между предприятиями.
Задача 5.
Определить нижнюю и верхнюю цену игры, заданной платежной матрицей А.
Методические указания к решению задачи: для проверки решения задачи используйте сервис Цена игры онлайн.
Задача 6.
Возможно строительство четырех типов электростанций: А1 (тепловых), А2 (приплотинных), А3 (бесшлюзовых) и А4 (шлюзовых). Эффективность каждого из типов зависит от различных факторов: режима рек, стоимсоти тплива и его перевозки и т.п. Предположим, что выделено четыре различных состояния,
каждое из которых означает определенное сочетание фаткоров, влияющих на эффективность энергетических объектов. Экономическая эффективность строительства отдельных типов электростанций изменяется в зависимости от состояния природы и задана матрицей А. определить оптимальное решение, опираясь на:
а) критерий Вальда;
б) критерий Сэвиджа;
в) критерий Гурвица;
г) предположение о равновероятных состояниях природы ( p1 = .. = p4 = 0,25)
Методические указания к решению задачи: для проверки решения задачи используйте сервис Оптимальное решение в играх с природой.
Задача № 1
Симплексный метод решения задач линейного программирования.
На предприятии выпускается n видов продукции Пj ( j=1,2,…, n). При ее изготовлении используются ресурсы R1, R2, R3. Размеры допустимых затрат ресурсов ограничены величинами b1,b2, b3. Расход ресурса Ri (i=1,2,3) на производство единицы производство единицы Пj равен аij. Прибыль от реализации единицы продукции Пj равна сij денежных единиц.
Необходимо найти оптимальный план выпуска продукции каждого вида с учетом имеющихся ограниченных ресурсов, который обеспечивал бы предприятию максимальную прибыль.
Задание
1. Составить математическую модель задачи.
2. Привести задачу к каноническому виду и заполнить симплекс – таблицу.
3. Построить исходное опорное решение, проверить его на оптимальность и, последовательно улучшая с помощью симплексных преобразований, найти оптимальное решение Хопт и fнаиб(Хопт).
4. Дать экономическое истолкование оптимальному решению и наибольшему значению целевой функции.
Решение:
Для решения используем данный сервис.
Задача № 2
Двойственная задача.
1. Сформулировать в экономических терминах двойственную задачу.
2. Составить математическую модель двойственной задачи, указав смысл двойственных переменных системы ограничений и целевой функции.
3. Используя оптимальное решение Хопт задачи № 1 и соответствие между парами двойственных переменных прямой и двойственной задач, найти компоненты yi оптимального решения Yопт двойственной задачи и значение целевой функции Gmin в двойственной задаче.
4. Дать экономическое истолкование величинеGmin, значениям основных и дополнительных переменныхyi в оптимальном решении Yопт двойственной задачи. Указать наиболее дефицитный и недефицитный (избыточный) ресурсы, если они имеются.
5. Пусть ресурсы взаимозаменяемы и из производства исключается 2 единицы ресурса (см. задание). Определить на сколько может уменьшиться максимальный доход. Найти, сколько единиц остальных ресурсов нужно ввести дополнительно в производство, чтобы компенсировать возможный убыток.
Решение.
Для решения используем сервис «Двойственная задача». Указываем количество переменных равным 4, количество ограничений – 3.
Скачать решение
Задача № 3
Транспортная задача.
На заводах А1 ,А2 ,А3 производится однородная продукция в количестве аi единиц. Четырем потребителям В1, В2, В3 , В4 требуется соответственно bj единиц готовой продукции. Расходы cij по перевозке единицы готовой продукции с завода Аi потребителю Вj заданы.
Необходимо найти план перевозок, минимизирующий общую стоимость перевозок.
Задание.
1. Ввести числовые данные транспортной задачи в распределительную таблицу и составить математическую модель.
2. Если транспортная задача открытого типа, то ее привести к задаче закрытого типа. Построить исходные планы перевозок по методу «северо–западного угла» и по методу наименьших стоимостей («двойного предпочтения»). Вычислить значения общих затрат для построенных планов и выявить, какой из планов лучше.
3. Методом потенциалов проверить план на оптимальность.
4. Последовательно улучшая план перевозок с помощью циклов пересчета в распределительной таблице, найти оптимальный план перевозок.
5. Определить по оптимальному плану перевозок:
1) количество продукции, отправляемого из каждого завода А1 ,А2 ,А3 каждому потребителю В1, В2, В3 , В4 ;
2) заводы Аi, в которых остается нераспределенная продукция, и указать ее объем;
3) пункты потребления Вj, которые недополучают продукцию, и указать ее количество.
Решение:
Воспользуемся данным сервисом. Указываем количество столбцов равным 4, количество строк – 3. Сначала выбираем метод нахождения опорного плана как «северо–западного угла», а затем «двойного предпочтения».
Скачать решение
Скачать решение
Задание. Для изготовления различных изделий А, и В предприятие использует три различных вида сырья. Нормы расхода сырья на производство одного изделия каждого вида, цена одного изделия А и В, а также общее количество сырья каждого вида, которое может быть использовано предприятием, приведены в табл.
Решение.
Решим прямую задачу линейного программирования симплекс-методом..
Определим максимальное значение целевой функции F(X) = 40x1 + 30x2 при следующих условиях-ограничений.
x1 + 3x2<=300
3x1 + 4x2<=477
4x1 + x2<=441
Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме).
В 1-м неравенстве смысла (<=) вводим базисную переменную x3. В 2-м неравенстве смысла (<=) вводим базисную переменную x4. В 3-м неравенстве смысла (<=) вводим базисную переменную x5.
1x1 + 3x2 + 1x3 + 0x4 + 0x5 = 300
3x1 + 4x2 + 0x3 + 1x4 + 0x5 = 477
4x1 + 1x2 + 0x3 + 0x4 + 1x5 = 441
Введем новую переменную x0 = 40x1 + 30x2.
Выразим базисные переменные <3, 4, 5> через небазисные.
x0 = 0+40x1+30x2
x3 = 300-x1-3x2
x4 = 477-3x1-4x2
x5 = 441-4x1-x2
Переходим к основному алгоритму симплекс-метода.
Поскольку задача решается на максимум, то переменную для включения в текущий план выбирают по максимальному положительному числу в уравнении для x0.
1. Проверка критерия оптимальности.
В выражении для x0 присутствуют отрицательные элементы. Следовательно, текущий план неоптимален
2. Определение новой базисной переменной.
max(40,30,0,0,0) = 40
x0 = 0+40x1+30x2
x3 = 300-x1-3x2
x4 = 477-3x1-4x2
x5 = 441-4x1-x2
В качестве новой переменной выбираем x1.
3. Определение новой свободной переменной.
Вычислим значения Di по всем уравнениям для этой переменной: bi / ai1
и из них выберем наименьшее:
min (300 : 1 , 477 : 3 , 441 : 4 ) = 1101/4
Вместо переменной x5 в план войдет переменная x1.
4. Пересчет всех уравнений.
Выразим переменную x1 через x5
x1 = 441/4-1/4x2-1/4x5
и подставим во все выражения.
x0 = 0+40(441/4-1/4x2-1/4x5)+30x2
x3 = 300-(441/4-1/4x2-1/4x5)-3x2
x4 = 477-3(441/4-1/4x2-1/4x5)-4x2
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = 4410+20x2-10x5
x3 = 759/4-11/4x2+1/4x5
x4 = 585/4-13/4x2+3/4x5
x1 = 441/4-1/4x2-1/4x5
Полагая небазисные переменные x = (3, 4, 1) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (0, -20, 0, 0, 10), x0 = 4410
1. Проверка критерия оптимальности.
В выражении для x0 присутствуют отрицательные элементы. Следовательно, текущий план неоптимален
2. Определение новой базисной переменной.
max(0,20,0,0,-10) = 20
x0 = 4410+20x2-10x5
x3 = 759/4-11/4x2+1/4x5
x4 = 585/4-13/4x2+3/4x5
x1 = 441/4-1/4x2-1/4x5
В качестве новой переменной выбираем x2.
3. Определение новой свободной переменной.
Вычислим значения Di по всем уравнениям для этой переменной: bi / ai2
и из них выберем наименьшее:
min (1893/4 : 23/4 , 1461/4 : 31/4 , 1101/4 : 1/4 ) = 45
Вместо переменной x4 в план войдет переменная x2.
4. Пересчет всех уравнений.
Выразим переменную x2 через x4
x2 = 45-4/13x4+3/13x5
и подставим во все выражения.
x0 = 4410+20(45-4/13x4+3/13x5)-10x5
x3 = 1893/4-23/4(45-4/13x4+3/13x5)+1/4x5
x1 = 1101/4-1/4(45-4/13x4+3/13x5)-1/4x5
После приведения всех подобных, получаем новую систему, эквивалентную прежней:
x0 = 5310-80/13x4-70/13x5
x3 = 66+11/13x4-5/13x5
x2 = 45-4/13x4+3/13x5
x1 = 99+1/13x4-4/13x5
Полагая небазисные переменные x = (3, 2, 1) равными нулю, получим новый допустимый вектор и значение целевой функции:
x = (0, 0, 0, 80/13, 70/13), x0 = 5310
Выражение для x0 не содержит положительных элементов. Найден оптимальный план.
Окончательный вариант системы уравнений:
x0 = 5310-80/13x4-70/13x5
x3 = 66+11/13x4-5/13x5
x2 = 45-4/13x4+3/13x5
x1 = 99+1/13x4-4/13x5
Оптимальный план можно записать так:
x3 = 66
x2 = 45
x1 = 99
F(X) = 5310
Анализ оптимальной симплекс-таблицы
В оптимальный план вошла дополнительная переменная x3. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 66Значение 0 в столбце x1 означает, что использование x1 - выгодно.
Значение 0 в столбце x2 означает, что использование x2 - выгодно.
Значение 62/13 в столбце x4 означает, что теневая цена (двойственная оценка) равна 62/13.
Значение 55/13 в столбце x5 означает, что теневая цена (двойственная оценка) равна 55/13.
Задание. Цех выпускает два вида продукции, используя два вида полуфабрикатов. Продукция используется при комплектовании изделий, при этом на каждую единицу продукции первого вида требуется не более двух единиц продукции второго вида. Нормы расхода полуфабрикатов каждого вида на единицу выпускаемой продукции, общие объемы полуфабрикатов и прибыль от единицы каждой продукции представлены в таблице. Определите план производства, обеспечивающий максимальную прибыль.
Решение.
Скачать решение в Excel
Задание. Найдите решение задачи симплексным методом, проиллюстрировав его графически. Составьте двойственную задачу и на основании теорем двойственности сделайте вывод о ее решении.
Решение.
Скачать решение
Пример. 1. Нефтяная компания "РТ" для улучшения эксплуатационных качеств и снижения точки замораживания дизельного топлива, которое она производит, добавляет в него определенные химикаты. В каждом бензобаке объемом 1000 л должно содержаться не менее 40 мг химической добавки X, не менее 14 мг химической добавки Y и не менее 18 мг химической добавки Z. Необходимые химические добавки в форме готовых смесей поставляют "РТ" две химические компании А и В. В нижеследующей таблице приведено содержание химических добавок в каждом продукте, поставляемом указанными компаниями.
| Продукт | Химические добавки, мг/л | ||
| X | Y | Z | |
| A | 4 | 2 | 3 |
| B | 5 | 1 | 1 |
Стоимость продукта А - 1,50 ф. ст. за 1 л, а продукта В - 3,00 ф. ст. за 1 л. Требуется: найти ассортиментный набор продуктов А и В, минимизирующий общую стоимость добавленных в топливо химикатов.
Рекомендации к решению: после составления экономико-математической модели задачи, ее можно будет решить симплекс-методом.
2. "Princetown Paints Ltd" выпускает три основных типа румян - жидкие, перламутровые и матовые - с использованием одинаковых смесеобразующих машин и видов работ. Главному бухгалтеру фирмы было поручено разработать для компании план производства на неделю. Информация о ценах продаж и стоимости 100 л товара приведена в таблице (ф. ст.).
| Румяна | |||
| Жидкие | Перламутровые | Матовые | |
| Цена продажи на 100 л | 120 | 126 | 110 |
| Издержки производства на 100 л: | |||
| Стоимость сырья | 11 | 25 | 20 |
| Стоимость трудозатрат | 30 | 36 | 24 |
| Стоимость приготовления смеси | 32 | 20 | 36 |
| Другие издержки | 12 | 15 | 10 |
Стоимость 1 чел.-ч составляет 3 ф. ст. а стоимость 1 ч приготовления смеси -4 ф. ст. Фонд рабочего времени ограничен 8000 чел.-ч. в неделю, а ограничение на фонд работы смесеобразующих машин равно 5900 ч. в неделю.
В соответствии с контрактными соглашениями компания должна производить 25000 л матовых румян в неделю. Максимальный спрос на жидкие румяна равен 35000 л в неделю, а на перламутровые румяна - 29000 л в неделю.
Требуется: определить оптимальные объемы производства в неделю, при которых достигается максимальное значение получаемой за неделю прибыли, и соответствующее значение прибыли.
Методические рекомендации к решению: необходимо составить экономико-математическую модель задачи, после чего решить симплекс-методом в Excel.
3. Компания "Bermuda Paint" - частная промышленная фирма, специализирующаяся на производстве технических лаков. Представленная ниже таблица содержит информацию о ценах продажи и соответствующих издержках производства единицы полировочного и матового лаков.
| Лак | Цена продажи 1 галлона, ф. ст. | Издержки производства 1 галлона, ф. ст. |
| Матовый | 13,0 | 9,0 |
| Полировочный | 16,0 | 10,0 |
Для производства 1 галлона матового лака необходимо затратить 6 мин трудозатрат, а для производства одного галлона полировочного лака - 12 мин. Резерв фонда рабочего времени составляет 400 чел.-ч. в день. Размер ежедневного запаса необходимой химической смеси равен 100 унциям, тогда как ее расход на один галлон матового и полировочного лаков составляет 0,05 и 0,02 унции соответственно. Технологические возможности завода позволяют выпускать не более 3000 галлонов лака в день.
В соответствии с соглашением с основным оптовым покупателем компания должна поставлять ему 5000 галлонов матового лака и 2500 галлонов полировочного лака за каждую рабочую неделю (состоящую из 5 дней). Кроме того, существует профсоюзное соглашение, в котором оговаривается минимальный объем производства в день, равный 2000 галлонов. Администрации данной компании необходимо определить ежедневные объемы производства каждого вида лаков, которые позволяют получать максимальный общий доход.
Требуется: определить ежедневный оптимальный план производства и соответствующую ему величину дохода.
Методические рекомендации к решению: необходимо составить экономико-математическую модель задачи, после чего решить симплекс-методом в Excel.
4. Три завода поставляют некоторую разновидность стали на пять торговых складов. Спрос каждого торгового склада в декабре, наличие стали на заводах, а также значения стоимости транспортировки 1 т стали приведены в нижеследующей таблице.
| Завод | Транспортные издержки, ф. ст. за единицу Торговый склад | Предложение т | ||||
| 1 | 2 | 3 | 4 | 5 | ||
| A | 20 | 27 | 33 | 25 | 34 | 200 |
| B | 22 | 36 | 34 | 28 | 26 | 250 |
| C | 26 | 29 | 27 | 26 | 28 | 300 |
| Потребность, т | 100 | 150 | 200 | 100 | 200 | |
Требуется определить минимальную стоимость транспортировки на декабрь.
Методические рекомендации к решению: проверить решение можно с помощью сервиса транспортная задача.
5. Администрация деревоперерабатывающего предприятия "Vibra" приняла на работу пять человек. Каждый из них имеет различные способности и навыки и затрачивает различное время на выполнение определенной работы. В настоящее время необходимо выполнить пять видов работ. Время выполнения работы каждым работником приведено в таблице:
| Работник | Время выполнения, ч | ||||
| Работы 1 | Работы 2 | Работы 3 | Работы 4 | Работы 5 | |
| М1 | 25 | 16 | 15 | 14 | 13 |
| М2 | 25 | 17 | 18 | 23 | 15 |
| М3 | 30 | 15 | 20 | 19 | 14 |
| М4 | 27 | 20 | 22 | 25 | 12 |
| М5 | 29 | 19 | 17 | 32 | 10 |
Требуется назначить на каждый вид работы одного из работников. Как это нужно сделать, чтобы общее время, необходимое для завершения всех видов работ, было минимальным?
Методические рекомендации к решению: данный тип задач относится к задачам о назначении.
6. Механический завод при изготовлении двух типов деталей использует токарное, фрезерное и сварочное оборудование. При этом обработку каждой детали можно вести двумя различными технологическими способами. Полезный фонд времени работы каждой группы оборудования (в станко-часах), нормы расхода времени при обработке детали на соответствующем оборудовании по данному технологическому способу и прибыль от выпуска единицы деталей каждого вида даны в таблице.
| Оборудование | Детали | Полезный фонд времени, станко-ч. | |||
| 1 | 2 | ||||
| Технологические способы | |||||
| 1 | 2 | 1 | 2 | ||
| Фрезерное | 2 | 2 | 3 | 0 | 20 |
| Токарное | 3 | 1 | 1 | 2 | 37 |
| Сварочное | 0 | 1 | 1 | 4 | 30 |
| Прибыль, усл. ед. | 11 | 6 | 9 | 6 | |
Составить оптимальный план «загрузки оборудования», обеспечивающий заводу максимальную прибыль.
Решение.
Обозначим через xij объем выпуска i-й детали j-м технологическим способом.
Блок ограничений на ресурсы представлен ограничениями на количество рабочего времени каждого станка:
фрезерный: (2x11 + 2x12) + (3x21) ≤ 20,
токарный: (3x11 + x13) + (x21 + 2x22) ≤ 37,
сварочный: (x12) + (x22 + 4x23) ≤ 30.
Построим целевую функцию. Задача состоит в максимизации прибыли компании. Поэтому в качестве целевой функции получим следующее выражение:
11x11 + 6x12 + 9x21 + 6x22 → max
Симплекс-метод. Компания производит полки для ванных комнат двух размеров – А и В. Агенты по продаже считают, что в неделю на рынке может быть реализовано до 550 полок. Для каждой полки типа А требуется 2 м2 материала, а для полки типа В – 3 м2 материала. Компания может получить до 1200 м2 материала в неделю. Для изготовления одной полки типа А требуется 12 мин машинного времени, а для изготовления одной полки типа В – 30 мин; машину можно использовать 160 час в неделю. Если прибыль от продажи полок типа А составляет 3 денежных единицы, а от полок типа В – 4 денежных единицы, то сколько полок каждого типа следует выпускать в неделю, чтобы получить максимальную прибыль?
Перейти к онлайн решению своей задачи
Задача коммивояжера. Коммивояжер должен объездить 6 городов. Для того чтобы сократить расходы, он хочет построить такой маршрут, чтобы объездить все города точно по одному разу и вернуться в исходный с минимумом затрат. Исходный город A. Затраты на перемещение между городами заданы следующей матрицей:
| A | B | C | D | E | F | |
| A | ∞ | 26 | 42 | 15 | 29 | 25 |
| B | 7 | ∞ | 16 | 1 | 30 | 25 |
| C | 20 | 13 | ∞ | 35 | 5 | 0 |
| D | 21 | 16 | 25 | ∞ | 18 | 18 |
| E | 12 | 46 | 27 | 48 | ∞ | 5 |
| F | 23 | 5 | 9 | 5 | ∞ |
Решение проводим с помощью данного сервиса. Указываем количество городов равное 6. Метод решения - метод ветвей и границ.
Скачать решение
Транспортная задача. Из трех холодильников Ai (i =1,3), вмещающих мороженную рыбу в количествах ai(тонн), необходимо последнюю доставить в пять магазинов Bj (j =1,5) в количествах bj(тонн). Стоимости перевозки 1 тонны рыбы из холодильника Ai в магазин Bj заданы в виде матрицы C=((cij)) (3x5). Написать математическую модель задачи и спланировать перевозки так, чтобы их общая стоимость была минимальной.
а1= 320, а2= 280, а3= 250,
b1= 150, b2= 140, b3= 110, b4= 230, b5= 220,

Перейти к онлайн решению своей задачи
Пример. 1. Решите задачу о диете со следующими данными. Из продуктов трех видов необходимо составит рацион минимальной стоимости, соблюдя при этом ограничения по содержанию некоторых витаминов. Данные приведены в таблице:

5. Приведите следующие задачи к каждой из канонических форм, описанным в лекции:
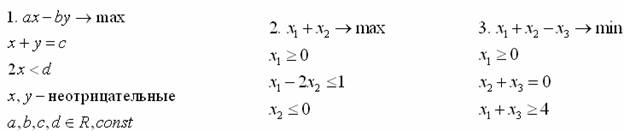
1. Докажите лемму 1, следствие из нее и признак оптимальности в краткой форме.
4. Постройте двойственные задачи к задачам из упражнения №3 прошлой лекции, сформулируйте для них условия признака оптимальности. Достаточно ли этих условий, чтобы найти решения задач?
Задачи из упражнения №3:
2. Решите задачу линейного раскроя со следующими данными. Для комплектации одного изделия необходимо две детали первого типа и одна деталь второго типа. Материал поступает в виде стандартных полос длиной 1 м. Деталь первого типа требует 15 см. материала, а деталь второго типа — 35 см.
3. В условиях предыдущей задачи, насколько важны для математической постановки данные о комплектности деталей в одном изделии? Как изменится математическая постановка, если понятие «две детали первого типа» заменить одной деталью первого типа, на изготовление которой уходит 2х15=30 см. материала?
1. Сформулируйте алгоритм одного шага процедуры последовательного улучшения для задачи в канонической форме 1, воспользовавшись результатами, полученными для формы 3 (перейдите в общем виде от формы 1 к форме 3).
1. Для следующих задач линейного программирования запишите двойственные к ним и найдите оптимальные решения.
3x1+2x2+x3 → max
2x1-x2+x3 ≤ 1
-x1+x2-x3 ≤ b2
x1-2x2+x3 ≤ 2
2x1+x2-3x3 ≤ b4
xi - свободные
2. Для следующих задач линейного программирования найдите оптимальные решения в зависимости от указанных параметров (величины некоторых ограничений) и проведите исследование изменения оптимального решения и оптимального значения целевой функции при изменении параметра
x1+2x2+3x3-x4 → max
x1-3x2-x3-2x4 = -4
x1-x2+x3 = 0
xi≥0
3. Для следующих содержательных постановок постройте математическую модель в виде задачи линейного программирования, приведите ее к какой-либо известной вам канонической форме, сформулируйте двойственную задачу и условия признака оптимальности, найдите решения пары двойственных задач, проинтерпретируйте двойственные оценки.
1) Нефтеперерабатывающий завод производит за месяц 1 500 000 л.алкилата, 1 200 000 л.крекинг-бензина и 1 300 000 л.изопентола. В результате смешивания этих компонентов в пропорциях 1:1:1 и 3:1:2 получается бензин сортов А и Б, соответственно. Стоимость 1000 л. бензина сорта А и Б, соответственно, равна 90 и 120 ед. Определить месячный план производства бензина сорта А и Б, максимизирующий стоимость выпущенной продукции.
1.5
Решите следующие задачи выпуклого программирования. Дайте интерпретацию двойственным переменным и проинтерпретируйте выполнение условий дополняющей нежесткости. Как изменится оптимальное решение при изменении правых частей ограничений?
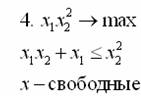
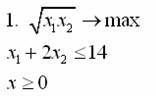
2.1
1. Для данных множеств исходов и описанных предпочтений выясните, являются ли предпочтения рациональными и можно ли их представить функцией полезности?
![]()
2. В предыдущем упражнении найдите результат выбора, если он существует.
2.2
1. Решение о покупке автомобиля. Рассмотрим простую ситуацию: человек, располагающий запасом денег W решает, приобрести ли автомобиль по цене p, его полезность измеряется в деньгах и денежная оценка факта наличия у него автомобиля для человека составляет ![]() (итого при покупке автомобиля его выигрыш составит
(итого при покупке автомобиля его выигрыш составит ![]() , а в отсутствие автомобиля просто измеряется размером богатства W). Представьте ситуацию в виде дерева решений. Найдите граничное значение цены автомобиля, при котором человеку безразлично — покупать автомобиль или нет.
, а в отсутствие автомобиля просто измеряется размером богатства W). Представьте ситуацию в виде дерева решений. Найдите граничное значение цены автомобиля, при котором человеку безразлично — покупать автомобиль или нет.
6. Задача выбора количества потребляемых товаров при бюджетном ограничении. Потребитель распределяет весь свой доход между потреблением некоторого обычного товара в количестве x≥0, покупая его по цене p руб. за единицу, и потреблением всех остальных товаров, рассматривая его, как денежный остаток, который он не тратит на первый товар, — z≥0. Полезность потребителя задана функцией u(x,z)=ln(x)+z, а множество доступных альтернатив задано бюджетным множеством в виде px+z≤R, x≥0, z≥0, где R — весь доход потребителя. Найдите оптимальный выбор потребителя в зависимости от параметров: ![]() . Являются ли предпочтения потребителя рациональными (поясните)? Каков содержательный смысл двойственной оценки бюджетного ограничения в такой задаче?
. Являются ли предпочтения потребителя рациональными (поясните)? Каков содержательный смысл двойственной оценки бюджетного ограничения в такой задаче?
2.3
1. В рассмотренную игру 2 (научно-исследовательские работы) введите учет дисконтирования, если дополнительно известно, что исследования длятся 1 год, а после налаживание производства происходит еще в течение 2 лет, а ежегодный коэффициент дисконтирования для фирмы составляет δ=0.85. Изменится ли результат принятия решения?
6. Предпочтения судовладельца описываются функцией полезности типа Неймана—Моргенштерна с элементарной функцией полезности от богатства х вида u(х), причем u имеет положительную убывающую производную. Он владеет богатством $40 000 и может потерять в случае аварии судна $10 000.
(A) Пусть вероятность аварии равна 0,02 и известно, что он застраховался на сумму $9 000. Возможно ли, что цена страхования на $1 равна $0,02? Если нет, то больше или меньше, чем $0,02? Объясните.
(B) Пусть цена страхования на $1 равна $0,02 и известно, что он застраховался на сумму $11000. Возможно ли, что вероятность аварии равна 0,02? Если нет, то больше или меньше, чем 0,02? Объясните.
(C) Пусть вероятность аварии равна 0,01 и известно, что цена страхования на $1 равна $0,02. Возможно ли, что он застраховался на сумму $10 000? Если нет, то больше или меньше, чем $10 000? Объясните.
2.4
1. Игра «Вахтер». На входе в некоторое учреждение стоит вахтер. В учреждение могут войти посетители двух типов: «свои» и «чужие» (будем их для краткости обозначать A и B). Некоторые посетители кажутся вахтеру своими, а некоторые — чужими (фактически, в игре есть 2 типа вахтера — обозначим их соответственно a и b). Вахтер точно не знает, «свой» перед ним или «чужой» и может только проверить у посетителя наличие пропуска. При этом если посетитель окажется своим, то выигрыш вахтера составит –1, а если чужим, то 1. Если вахтер пропускает человека без проверки, то ему уже все равно, свой тот или нет, и выигрыш вахтера составляет 0.
Опишите игру в виде дерева решений «единого вахтера», который не обращает внимания на то, что ему кажется и в виде дерева, в котором учтены подозрения вахтера (a и b). Как вахтеру использовать свои подозрения при принятии решения проверять или не проверять документы?