Вычисление приближенно с помощью дифференциала
С одной стороны, вычисление дифференциала значительно проще, чем вычисление приращения, с другой стороны, dy≈∆y и допускаемая при этом погрешность может быть сделана сколь угодно малой за счет уменьшения ∆x. Эти обстоятельства позволяют во многих случаях заменять ∆y величиной dy. Из приближенного равенства dy≈∆y, учитывая, что ∆y = f(x) – f(x0), а dy=f’(x0)(x-x0), получимf(x) ≈ f(x0) + f’(x0)(x–x0), (1)Пример№1. Вычислить
.
Решение. Взяв функцию
, имеем: 
. Полагая x0=16 (выбираем сами, чтобы корень извлекался), ∆x = 0,02, получим:
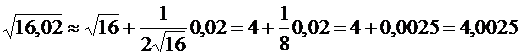
Пример №2. Вычислить значение функции f(x) = ex в точке x=0.1.
Решение. В качестве x0 возьмем число 0, то есть x0=0, тогда ∆x=x-x0 =0.1 и e0.1≈e0 + e00.1 = 1+0.1 = 1.1. По таблице e0.1≈1.1052. Ошибка получилась незначительная.
Отметим еще одно важное свойство дифференциала. Формула для нахождения дифференциала dy=f’(x)dx верна как в случае, когда x – независимая переменная, так и в случае, когда x – функция от новой переменной t. Это свойство дифференциала называется свойством инвариантности его формы. Например, для функции y=tg(x) дифференциал запишется в виде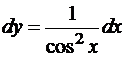 
независимо от того, является ли x независимой переменной или функцией. В случае, если x – функция и конкретно задана, например x=t2, то вычисление dy можно продолжить, для чего найдем dx=2tdt и подставим в ранее полученное выражение для dy:
.
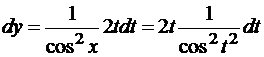Если вместо формулы (2) воспользовались бы неинвариантной формулой (1), то в случае, когда x – функция, мы не могли бы подобным образом продолжить вычисление dy, так как ∆x, вообще говоря, не совпадает с dx.
Пример №3
Извлечь квадратный корень из 3654.
Решение. Надо найти значение функции 
при x=3654. Легко вычисляются значения f(x) и 
при x=3600. Формула (1) при a=3600, h=54 дает 
. Здесь все знаки верны.
Пример №4. Найти 102,1.
Решение. Полагаем f(x)=10x , так что 
. Формула (1) при a=2, h=0,1 дат:
.
Этот результат грубоват (с точностью до четвертой значащей цифры 102,1=125,9).
Если таким же образом вычислить 102,01 (теперь h=0,01), получим 102,3. Здесь все знаки верны.
Пример №5. Найти без таблиц tg 46о.
Решение. Полагаем f(x)=tg x, a=45о, h=1о=0,0175 радиана; тогда имеем: 
. Значит, tg 45о=1+2·0,0175=1,0350.
Неверен только последний знак; из таблиц имеем tg 46o=1, 0355.
Полезно заметить следующие приближенные формулы (a-малая величина):
, 
; (2)
, 
; (3)
, 
; (4)
, 
; (5)
, 
; (6)
Формулы (2)-(6) являются частными случаями формулы (1+a)n≈1+na; последняя получается из (1), если положить f(x)=xn, a=1,h=a.
ln(1+a)≈a, ln(1-a)≈-a; (7)
ea≈1+a, 
; (8)
sin a≈a, 
, tg a≈a; (9)