Кратные и криволинейные интегралы
№ 1.Вычислить двойной интеграл по указанному прямоугольнику D: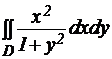 , где D – прямоугольник
, где D – прямоугольник 0≤x≤2, 0≤y≤1.
Преобразуем двойной интеграл в повторный. Пределы интегрирования известны, поэтому
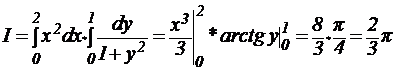
№ 2.Вычислить двойной интеграл по области G, ограниченной указанными линиями:
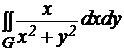 , где область G – параболический сегмент, ограниченный параболой y=½x² и прямой y=x.
, где область G – параболический сегмент, ограниченный параболой y=½x² и прямой y=x.
Изобразим область интегрирования G.
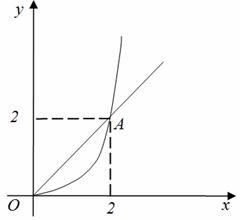
Так как прямая y=x и парабола y=½x² пересекаются в точках O(0;0) и A(2;2), то область G определяется системой неравенств:
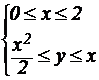
Теперь вычислим искомый интеграл I:
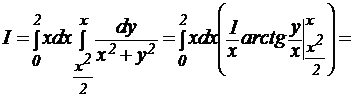
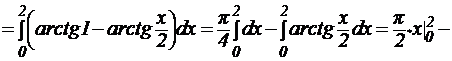
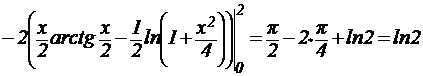 .
.
№ 3.Вычислить криволинейный интеграл:
1) ![]() , где L - дуга параболы
, где L - дуга параболы y2=2x, заключенная между точками (2;2) и (8;4). Найдем дифференциал дуги dl для кривой ![]() . Имеем
. Имеем
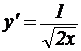 ,
, ![]() .
.
Следовательно, данный интеграл равен
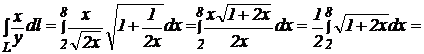
2) ![]() , где L - окружность
, где L - окружность x2+y2=a·x (a>0).
Введем полярные координаты x=r·cos(φ), y=r·sin(φ). Тогда, так как x2+y2=a·x, уравнение окружности примет вид r2=a·r·cos(φ), т.е. r=a·cos(φ), а дифференциал дуги
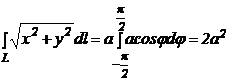 .
.
№ 4. Двойной интеграл ![]() выражает площадь области G. Вычислить площадь области G, если она ограниченна линиями:
выражает площадь области G. Вычислить площадь области G, если она ограниченна линиями: y2=2x и y=x.
Имеем ![]() . Направление, или порядок интегрирования выберем так, как указано на чертеже:
. Направление, или порядок интегрирования выберем так, как указано на чертеже:
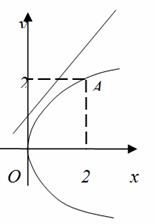
Сначала определим координаты точки пересечения прямой и параболы:
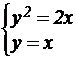 → x2=2x → x1=0, y1=0 и x2=2, y2=2.
→ x2=2x → x1=0, y1=0 и x2=2, y2=2.
Проекция области G на ось Oy есть отрезок [0;2]. Таким образом,
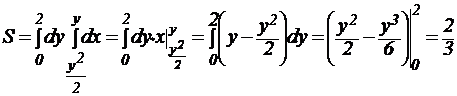
Центр тяжести однородной плоской фигуры
Пусть областью D плоскости xOy является материальная пластинка, масса которой распределяется с поверхностной плотностью p=f(x,y). Тогда масса M этой пластинки вычисляется по формулеКоординаты точки C(xc,yc), являющейся центром тяжести этой пластинки, определяются по формулам
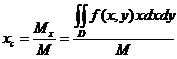 ,
, 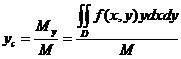 . (2)
. (2)
Если поверхностная плотность p постоянна (пластинка однородна), то из формулы (2) следует:
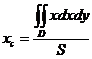 ,
, 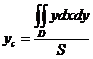 , (3)
, (3)
где S – площадь области D.
Пример. Найти координаты центра тяжести однородной плоской фигуры, ограниченной параболой y=x2-2x-1 и прямой y=x-1 (рис.).
Решение
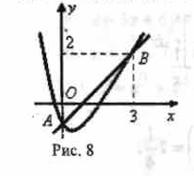
Вычислим площадь S данной фигуры с помощью двойного интеграла: ![]() .
.
Парабола и прямая пересекаются в точках A(0,-1) и B(3,2). Область D определяется неравенствами 0≤x≤3, x2-2x-1≤y≤x-1.
Тогда
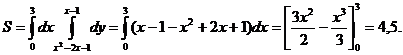
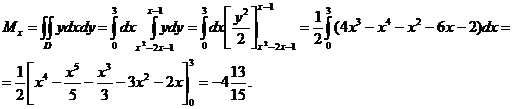
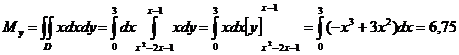
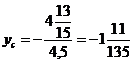 и точка
и точка