Производная функции
Производной функции y=f(x) в точке x0 называется конечный предел отношения приращения функции в этой точке к приращению аргумента при стремлении последнего к нулю (см. пример).Если необходимо найти производные функции нескольких переменных z=f(x,y), то можно воспользоваться данным онлайн-калькулятором. Решение оформляется в формате Word.
Правила ввода функции, заданной в явном виде
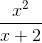 ≡ x^2/(x+2)
≡ x^2/(x+2)
cos2(2x+π) ≡ (cos(2*x+pi))^2
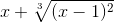 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)
Правила ввода функции, заданной в неявном виде
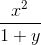 ≡ x^2/(1+y)
≡ x^2/(1+y)
cos2(2x+y) ≡ (cos(2*x+y))^2
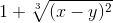 ≡ 1+(x-y)^(2/3)
≡ 1+(x-y)^(2/3)
Если функция задана в виде
y2-x=cos(y), то ее необходимо записать так: y^2-x-cos(y).Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
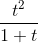 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
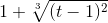 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Правила ввода функции, заданной в параметрическом виде
- Все переменные выражаются через t
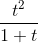 ≡ t^2/(1+t)
≡ t^2/(1+t)
cos2(t) ≡ cos(t)^2
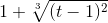 ≡ 1+(t-1)^(2/3)
≡ 1+(t-1)^(2/3)
Вместе с этим калькулятором также используют следующие:
Точки разрыва функции
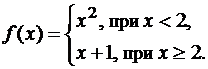

Решение пределов
Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных
Вычисление интегралов
Точки разрыва функции
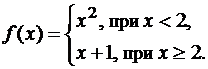

Решение пределов
Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных
Вычисление интегралов
Таблица производных
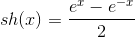 – гиперболический синус
– гиперболический синус
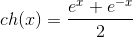 – гиперболический косинус
– гиперболический косинус
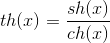 – гиперболический тангенс
– гиперболический тангенс
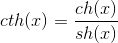 – гиперболический котангенс
– гиперболический котангенс
- (xα)’ = α xα-1
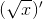 = 1/2x1/2 =
= 1/2x1/2 = 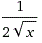
- (ax)’ = ax·lna
- (ex)’ = ex
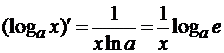
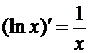
- (sinx)’ = cosx
- (cosx)’ = -sinx
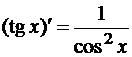
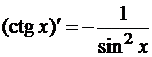
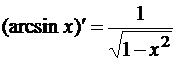
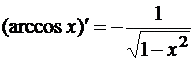
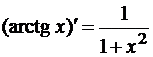
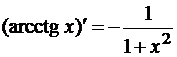
- (shx)’ = chx
- (chx)’ = shx
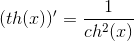
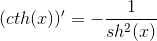
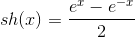 – гиперболический синус
– гиперболический синус
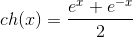 – гиперболический косинус
– гиперболический косинус
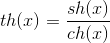 – гиперболический тангенс
– гиперболический тангенс
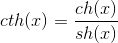 – гиперболический котангенс
– гиперболический котангенс
Как найти производную, исходяя из ее определения?
Правила нахождения производных
Пример 1. Найти производную функцииy=cos4x.
Решение.
Внешней функцией здесь служит степенная функция: cos(x) возводится в четвертую степень. Дифференцируя эту степенную функцию по промежуточному аргументу cos(x), получим
(cos4x)′cos x = 4cos4-1x = 4cos3x
но промежуточный аргумент cos(x) – функция независимой переменной х; поэтому надо полученный результат умножить на производную от cos(x) по независимой переменной х . Таким образом, получим
y′x = (cos4x)′cos x·(cosx)′x = 4·cos3x·(-sin x) = -4·cos3x·sin x
При дифференцировании функций нет необходимости в таких подробных записях. Результат следует писать сразу, представляя последовательно в уме промежуточные аргументы.
Пример 2. Найти производную функции
![]() .
.
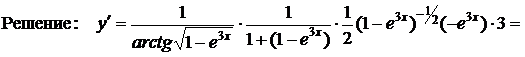
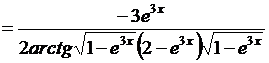 .
.
В некоторых случаях, если, например, нужно найти производную функции
y = (u(x))v(x), или функции, заданной в виде произведения большого числа сомножителей, используется так называемый способ логарифмического дифференцирования.
Пример 3. Найти производную функции
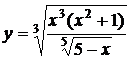 .
.
Решение.
Применим метод логарифмического дифференцирования. Рассмотрим функцию
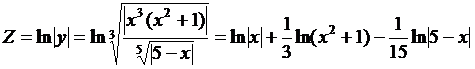
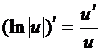 , будем иметь
, будем иметь
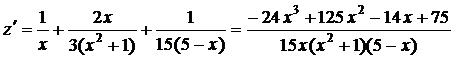
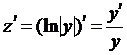 , откуда
, откуда
 .
.
Пример 4. Найти производную функции y=xex
Решение.
![]()
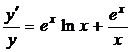 ;
;
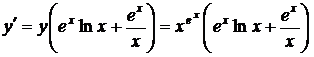 .
.
Прикладное использование производной
Вычисление производной первого и второго порядка используется во многих прикладных задачах. Рассмотрим наиболее распространенные из них.- Нахождение экстремумов функции одной переменной осуществляют приравниванием к нулю производной:
f'(x)=0. Этот этап является основным для построения графика функции методом дифференциального исчисления. - Значение производной в точке x0 позволяет находить уравнение касательной к графику функции.
- Отношение производных позволяет вычислять пределы по правилу Лопиталя.
- В математической статистике плотность распределения f(x) определяют как производную от функции распределения F(x).
- При отыскании частного решения линейного дифференциального уравнения требуется вычислять производную в точке.
- В методе Ньютона с помощью производной отделяют корни нелинейных уравнений.