Закон распределения дискретной случайной величины
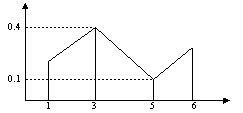
В задачах 12.1-12.10 требуется найти: а) математическое ожидание; б) дисперсию; в) среднее квадратическое отклонение дискретной случайной величины X по заданному закону её распределения, заданному таблично (в первой строке таблицы указаны возможные значения, во второй строке – вероятности возможных значений).Закон распределения дискретной случайной величины можно изобразить графически. С этой целью на прямоугольной системе координат строят точки M1(x1; p1), M2(x2; p2), …, Mn(xn; pn), где xi – возможные значения случайной величины, а pi – соответствующие вероятности, и соединяют их последовательно отрезками прямых. Полученную фигуру называют многоугольником распределения. Построим многоугольник распределения дискретной случайной величины X, заданной следующим законом распределения:
| X | 1 | 3 | 5 | 6 |
| p | 0,2 | 0,4 | 0,1 | 0,3 |
Математическое ожидание:
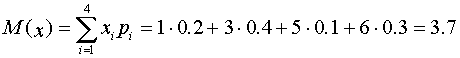
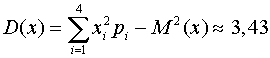 .
.
Среднее квадратическое отклонение: ![]() .
.