Математическое ожидание непрерывной случайной величины. Пример решения
Найти:
а) параметр A;
б) функцию распределения F(x);
в) вероятность попадания случайной величины X в интервал [1;2];
г) математическое ожидание MX и дисперсию DX.
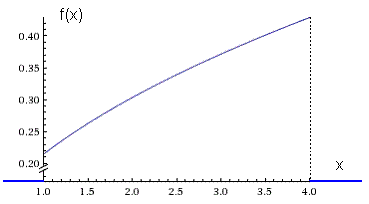
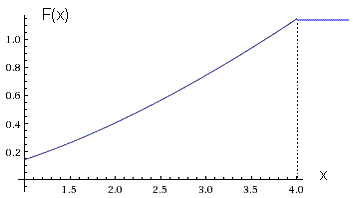
Построить график функций f(x) и F(x).
Решение.
Задание 2. Найти дисперсию случайной величины X, заданной интегральной функцией.
Задание 3. Найти математическое ожидание случайной величины Х заданной функцией распределения.
Перейти к онлайн решению своей задачи
Задание 4. Плотность вероятности некоторой случайной величины задана следующим образом:
f(x) = A/x4 (x = 1; +∞)
Найти коэффициент A, функцию распределения F(x), математическое ожидание и дисперсию, а также вероятность того, что случайная величина примет значение в интервале [0,2]. Построить графики f(x) и F(x).
Задача. Функция распределения некоторой непрерывной случайной величины задана следующим образом:
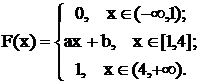
Определить параметры a и b, найти выражение для плотности вероятности f(x), математическое ожидание и дисперсию, а также вероятность того, что случайная величина примет значение в интервале [2,3]. Построить графики f(x) и F(x).
F′=f(x)=a
Зная, что
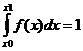найдем параметр a: 
или 3a=1, откуда a = 1/3
Параметр b найдем из следующих свойств:
F(4) = a*4 + b = 1
1/3*4 + b = 1 откуда b = -1/3
Следовательно, функция распределения имеет вид: F(x) = (x-1)/3
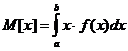
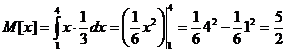
Дисперсия.
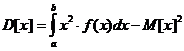
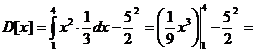1/9•43 - (1/9•13) - (5/2)2 = 3/4
Найдем вероятность того, что случайная величина примет значение в интервале [2,3]
P(2 < x< 3) = F(3) – F(2) = (1/3*3 - 1/3) - (1/3*2 - 1/3) = 1/3
Пример №1. Задана плотность распределения вероятностей f(x) непрерывной случайной величины X. Требуется:
- Определить коэффициент A.
- найти функцию распределения F(x).
- схематично построить графики F(x) и f(x).
- найти математическое ожидание и дисперсию X.
- найти вероятность того, что X примет значение из интервала (2;3).
Решение:
Случайная величина Х задана плотностью распределения f(x):
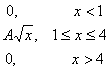
Найдем параметр A из условия:
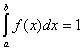
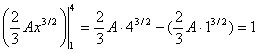
или
14/3*A-1 = 0
Откуда,
A = 3/14
Функцию распределения можно найти по формуле.
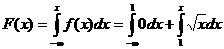
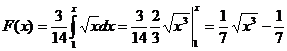
Математическое ожидание находится по следующей формуле:
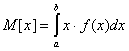
Дисперсия выражена формулой:
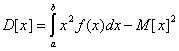
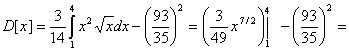3/49•47/2 - (3/49•17/2) - (93/35)2 = 876/1225
Вероятность того, что X примет значение из интервала (2;3):
Пример №2. Случайная величина X задана функцией распределения F(x). Найти плотность распределения вероятностей, математическое ожидание и дисперсию случайной величины. Схематично построить графики функций F(x) и f(x).