Приемы нахождения неопределенных интегралов
Простейшие преобразования подынтегрального выражения
Многие интегралы легко вычисляются, если произвести простейшие преобразования, например, выделить целую часть, преобразовать тригонометрическое выражение и так далее. Поясним сказанное на примерах.Примеры
1. 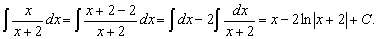
2.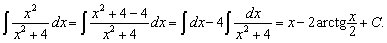
3.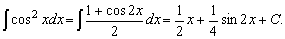
2.
3.
Пример. Найти неопределенный интеграл, используя метод разложения на простейшие дроби.
1. ![]()
Решение. Используем метод разложения на простейшие. Разложим функцию на простейшие слагаемые:
x+2 = Ax(x-1) + B(x-1) + Cx2
A + С = 0
-A + B = 1
-B = 2
Решая ее, находим:
A = -3;B = -2;C = 3;
Далее интегрируем дроби, используя стандартную таблицу интегрирования.
2. ![]()
Решение.
1. Делим первый элемент делимого на старший элемент делителя, помещаем результат под чертой
2.
| x5 + 1 | x2 - 1 |
| x5 - x3 | x3 |
| x3 + 1 |
| x5 + 1 | x2 - 1 |
| x5 - x3 | x3 + x2 |
| x3 + 1 | |
| x3 - x | |
| x + 1 |
Целая часть: x + 1
Остаток: x + 1
Далее интегрируем дроби, используя стандартную таблицу для интегралов.
Сложные дроби, в которых степень числителя больше степени знаменателя упрощаются посредством деления столбиком.
Также рекомендуется изучить сервис вычисление интегралов онлайн
Замена переменной при вычислении интегралов
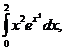 , t=x3
, t=x3
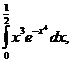 ,-x4=t
,-x4=t
![]()
![]()
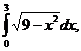 , x=3sint
, x=3sint
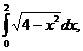 , x=2sint
, x=2sint
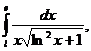 , lnx=t
, lnx=t
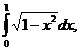 , x=sint
, x=sint
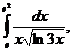 , ln3x=t
, ln3x=t
![]() , 5+4x=t
, 5+4x=t