Раскрытие неопределенности по правилу Лопиталя
Дифференциальное исчисление значительно облегчает задачу раскрытия неопределенностей при вычислении пределов. Простой прием раскрытия неопределенностей видаТеорема. Предел отношения двух бесконечно малых или бесконечно больших функций при x → x0 равен пределу отношения их производных, если последний существует, то есть
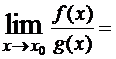
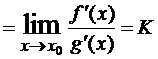 (K может быть конечным и бесконечным).
(K может быть конечным и бесконечным).
Другой вид неопределенность 0/0
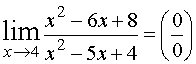 можно раскрыть другим методом.
можно раскрыть другим методом.
Пример №2. Найти ![]() .
.
Решение. 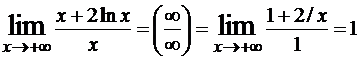 .
.
Пример №3. Найти 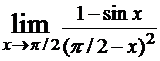 .
.
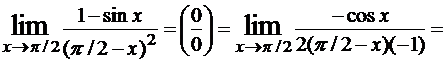
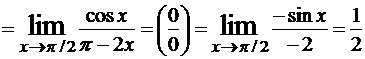 .
.
Замечание 1. Применяя неоднократно правило Лопиталя, нужно каждый раз проверять, не раскрылась ли уже неопределенность, иначе можно получить неверный результат.
Замечание 2. В теореме требование существования 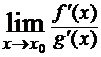 является существенным, так как если он не существует, то это не означает, что
является существенным, так как если он не существует, то это не означает, что 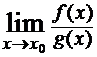 тоже не существует. Например,
тоже не существует. Например, 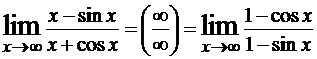 – не существует, однако
– не существует, однако 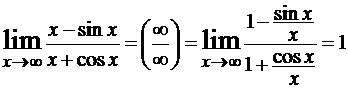 .
.
Неопределенность 0·∞ возникает, если требуется найти
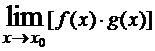 при условии
при условии 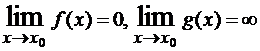 . В результате преобразования
. В результате преобразования 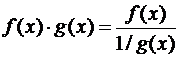 (либо
(либо 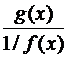 ) получается неопределенность 0/0 (либо ∞/∞).
) получается неопределенность 0/0 (либо ∞/∞).
Если нужно найти
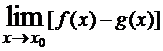 , причем
, причем 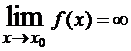 и
и 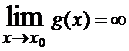 , то, представив разность f(x) – g(x) =
, то, представив разность f(x) – g(x) = 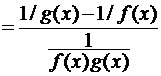 , получим неопределенность 0/0. Неопределенности вида 00, 1∞, ∞0 путем логарифмирования выражения [f(x)]g(x)сводятся к неопределенности 0·∞, рассмотренной выше.
, получим неопределенность 0/0. Неопределенности вида 00, 1∞, ∞0 путем логарифмирования выражения [f(x)]g(x)сводятся к неопределенности 0·∞, рассмотренной выше.
Пример №4. Найти ![]() .
.
Решение. Здесь имеем неопределенность 0·∞. Перепишем данное выражение в виде 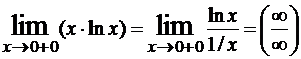 .
.
Теперь можно применить правило Лопиталя:
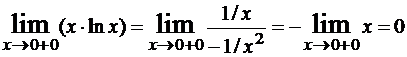 .
.Перейти к онлайн решению своей задачи
Пример №5. Найти ![]() .
.
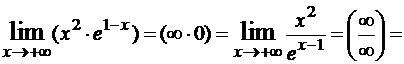
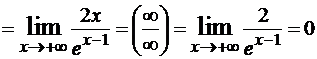 .
.
Пример №6. Найти 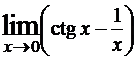 .
.
Решение.Данное выражение представляет собой неопределенность вида ∞-∞. Преобразуем его к другому виду:

Пример №7. Найти ![]() .
.
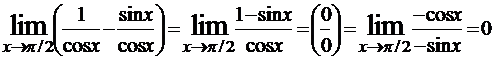 .
.Пример №8. Найти ![]() .
.
Решение.Здесь неопределенность вида 00. Обозначим y=xx и прологарифмируем: lny = x·lnx, откуда в силу непрерывности логарифмической функции ![]() (пример 4). Итак,
(пример 4). Итак, ![]() , откуда
, откуда ![]() , т.е.
, т.е. ![]() .
.
Пример №9. Найти 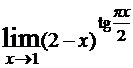 .
.
Решение.Имеем неопределенность 1∞, которую можно было бы раскрыть с помощью второго замечательного предела, однако мы иллюстрируем другой прием. Обозначим 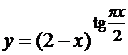 , тогда
, тогда
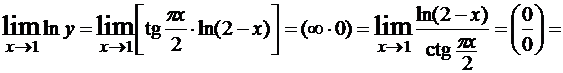
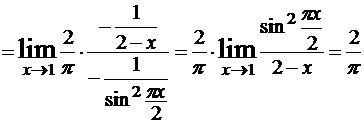 .
.
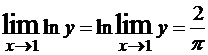 , тогда по определению логарифма
, тогда по определению логарифма Пример №10. Найти предел, используя правило Лопиталя–Бернулли: 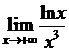 .
.
Решение.
Функция f(x)=ln(x) дифференцируема на всей области определения, функция φ(x) = x3 дифференцируема для любого x из R, при x→∞; x3→∞. Имеем неопределенность ![]() . Применяем правило Лопиталя–Бернулли:
. Применяем правило Лопиталя–Бернулли:
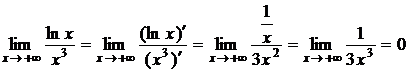 .
.Пример №11. Найти предел, используя правило Лопиталя–Бернулли:
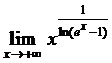 .
Решение. Логарифмируем функцию
.
Решение. Логарифмируем функцию 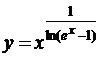 , получим:
, получим: 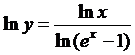 .
.
Функции ln(x) и ln(ex-1) дифференцируемы на (0;+∞). Применяем правило Лопиталя–Бернулли для неопределенности ![]() :
:
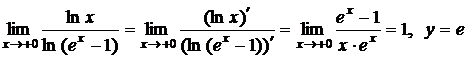 .
.Пример №12. Вычислите предел, применяя правило Лопиталя.
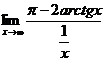
Решение. Для нашего примера:
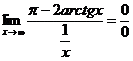
Для нашего примера:
f(x) = π-2arctg(x)
g(x) = 1/x
Находим первую производную
![]()
g'(x) = -1/x2
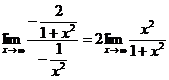
f’(x) = 2x
g’(x) = 2x
![]()
Ответ: 2
Пример №13. Используя правило Лопиталя, найдите пределы функции.
![]()
Решение. Записываем как: 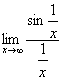
![]()
Для нашего примера:
f(x) = sin(1/x)
g(x) = 1/x
Находим первую производную
f'(x) = -(cos(1/x))/x2
g'(x) = -1/x2
![]()
Упростим:
![]()
Пример №14. Раскрыть неопределённости по правилам Лопиталя: ![]()
Представим в виде:
![]() Тогда можно записать как:
Тогда можно записать как:
![]()
Пример №15. Найти данный предел, используя правило Лопиталя.
![]()
Решение.
![]()
Для нашего примера:
f(x) = ln(1-2x)
g(x) = x
Находим первую производную
![]()
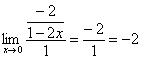
Пример №15. ![]()
Для нашего примера:
f(x) = e2x-1
g(x) = sin(x)
Находим первую производную
f'(x) = 2e2x
g'(x) = cos(x)