Системы дифференциальных уравнений
Система уравнений, связывающая независимую переменную, искомые функции и некоторое количество их производных, то есть система уравнений вида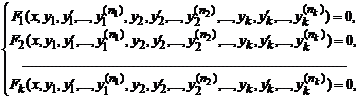
называется системой обыкновенных дифференциальных уравнений. Если эта система разрешена относительно старших производных y(n1)1 y(n2)2…, y(nk)k то она называется системой в канонической форме и имеет вид
yl(nl)=φl(x, y1, ..., yl(n1-1), y2, y2(n2-1), ... , yk, ... , yk(nk-1)), l=1,k. Эту систему путём введения новых неизвестных функций [9-11] можно привести к виду
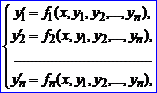 (40)
(40)
которая называется системой обыкновенных дифференциальных уравнений в нормальной форме или системой обыкновенных дифференциальных уравнений в форме Коши.
Если ввести в рассмотрение векторы y=(y1,y2,…,yn)T, f=(f1,f2,…,fn)T и вспомнить [1,3], что производная вектор-функции по скалярному аргументу вычисляется по формуле y'=(y1', y2',…, yn')T, то систему (40) можно записать в векторной форме y'=f(x,y), которая по виду совпадает с записью дифференциального уравнения первого порядка.
Для системы обыкновенных дифференциальных уравнений (40) можно поставить задачу Коши: найти решение (y1,y2,…,yn)T
системы (40), удовлетворяющее начальным условиям
(y1(x0), y2(x0), ... , yn(x0))T = (y10, y20, ... , yn0)T, (41)
В векторной форме условия (41) имеют вид y(x0)=y0.
Так же, как и для дифференциальных уравнений, для систем дифференциальных уравнений справедлива теорема существования и единственности.
Теорема. Если все функции fi, i=1,n, непрерывны по x и удовлетворяют условию Липшица по yi, i=1,n, то решение задачи Коши (40), (41) существует и единственно.
Доказательство этого результата опустим.
Если функции fi, i=1,n не зависят от x, то система (40) называется автономной. В этом случае обычно вместо x пишут t и систему записывают в виде
![]()
или в векторной форме y'=f(y). Если трактовать независимую переменную как время, то автономные системы отличаются тем, что их поведение не зависит от начала отсчёта переменной t, а зависит от начальной точки и времени, прошедшего с начала процесса. Действительно, сделав замену переменных τ=t-t0, получим
![]()
В общем случае для решения систем имеются методы интегрируемых комбинаций и исключения неизвестных. Как указывалось ранее, любое уравнение порядка n можно свести к системе n уравнений в нормальной форме. Возможна и обратная процедура. На этой идее и основан метод исключения неизвестных. Разберём его на примерах.
Примеры
1. Для системы дифференциальных уравнений
![]()
выражая y из второго уравнения, имеем y=-x'+cost, y'=-x''-sint. Подставляя в первое уравнение и приводя подобные, получаем уравнение x''+4x'+3x=0. Это линейное уравнение второго порядка с постоянными коэффициентами. Корни его характеристического уравнения r2 + 4r + 3 = 0 равны r1 = -3, r2 = -1.
Поэтому x=C1e-3t + C2e-t. Подставляя в выражение для y, получаем y=3C1e-3t + C2e-t + cost или в векторной форме 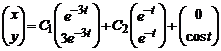 .
.
2. Найдём решение системы дифференциальных уравнений
![]()
Выражая из первого уравнения y получаем ![]() . Следовательно,
. Следовательно, ![]() и, подставляя во второе уравнение, имеем x''+9x=0. Это линейное уравнение второго порядка с постоянными коэффициентами. Корни его характеристического полинома r2+9 равны r1,2=±3i Поэтому общее решение полученного уравнения есть x=C1cos3t + C2sin3t. Подставляя в выражение для y, получаем
и, подставляя во второе уравнение, имеем x''+9x=0. Это линейное уравнение второго порядка с постоянными коэффициентами. Корни его характеристического полинома r2+9 равны r1,2=±3i Поэтому общее решение полученного уравнения есть x=C1cos3t + C2sin3t. Подставляя в выражение для y, получаем ![]() или в векторной форме
или в векторной форме 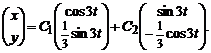
Системы линейных уравнений
Если в системе (40) все функции fi линейны по переменным y1,y2,..,yn, то она называется линейной. В этом случае её можно переписать в виде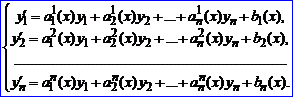 (42)
(42)
Обозначая матрицу системы через A(x), а вектор (b1(x),b2(x),…,bn(x))T через b(x) систему (42) можем переписать в матричной форме,
y'=A(x)y + b(x) (42а)
Будем, по возможности, пользоваться матричной формой записи. Если b(x)=0, то получаем соответствующую систему однородных уравнений
y'=A(x)y. (43)
Для систем линейных уравнений строится теория, полностью эквивалентная теории линейных уравнений порядка n. В частности, справедлива теорема о наложении решений и её следствия. В том числе и теорема о том, что множество решений однородной системы (43) образует линейное подпространство в пространстве дифференцируемых вектор-функций.
Так же как для векторов [1,2] и систем функций, для систем вектор-функций вводятся понятия их линейной зависимости и линейной независимости.
Определение.
Система вектор-функций y1,y2,…,ym называется линейно зависимой на отрезке [a,b], если существуют числа α1, α2,…, αm, , не все из которых равны нулю, такие, что
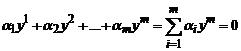
всюду на [a,b], и линейно независимой, если такого ненулевого набора не существует.
Рассмотрим совокупность вектор-функций y1,y2,…,ym. Определитель, составленный из их координат,
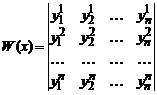
называется определителем Вронского, или вронскианом системы вектор-функций y1,y2,…,ym.
Определитель Вронского служит индикатором линейной зависимости системы вектор-функций.
Теорема. Если система вектор-функций линейно зависима, то её определитель Вронского W(x) равен нулю.
Теорема. Если y1,y2,…,ym - линейно независимая совокупность решений системы однородных уравнений y'=A(x)y, то её определитель Вронского W(x) отличен от нуля для всех x∈[α, β].
Удостоверимся в существовании базиса в пространстве решений системы уравнений y'=A(x)y.
Теорема. Для любой однородной системы линейных дифференциальных уравнений y'=A(x)y порядка n существует система n линейно независимых решений этого уравнения.
Доказательство. Возьмём матрицу
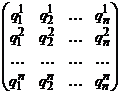 (44)
(44)
с определителем, отличным от нуля. Тогда строки и столбцы этой матрицы линейно независимы. Найдём такие решения yj(x), j=1,2,..,n, системы уравнений y'=A(x)y, чтобы выполнялись соотношения ykj(x0)=qkj, k=1,2,...,n. По теореме существования и единственности такой набор решений существует. Найденная система решений линейно независима, так как её определитель Вронского в точке x0 совпадает с определителем матрицы (44). Теорема доказана.
Матрицу (44) можно взять единичную.
Теорема (о виде общего решения однородной системы линейных дифференциальных уравнений). Если y1,y2,…,yn - линейно независимая совокупность решений однородной системы уравнений y'=A(x)y, то любое решение этой системы есть линейная комбинация решений y1,y2,…,yn, то есть
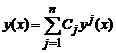
и, следовательно, y1,y2,…,yn - базис пространства решений системы уравнений y'=A(x)y.
см. также Решение системы линейных дифференциальных уравнений методом вариации произвольной постоянной