Однородные системы линейных дифференциальных уравнений с постоянными коэффициентами
Как и в случае линейных уравнений высших порядков, наиболее полно разработаны вопросы нахождения фундаментальной системы решений для однородных систем дифференциальных уравнений с постоянными коэффициентами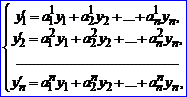
(5.45)
или в матричной форме
y'=Ay. (5.45а)
Будем искать решение системы (5.45) в виде
y=αert = (α1, α2,.., αn)Tert = (α1ert, α2ert,.., αnert)T (5.46)
Подставив это решение в (5.45), получаем равенство αrert =Aαert, откуда, сокращая на ert, можем записать αr = Aα или Aα-αr= Aα-Eαr = (A - rE)α =0. Последнее соотношение (A - rE)α =0 есть система для нахождения собственных чисел и собственных векторов матрицы A. Таким образом, y=αert - решение системы (5.45) тогда, когда r- собственное число, а α - ему соответствующий собственный вектор матрицы A. Возможны два случая: 1) все собственные числа различны; 2) есть кратные собственные числа. Разберём эти возможности по отдельности.
В первом случае имеем n решений
Эта система функций линейно независима, так как её определитель Вронского отличен от нуля. Действительно,
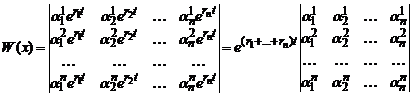
Во втором случае возможны два варианта. Пусть для собственного числа rj кратности k имеется k линейно независимых собственных векторов αj1, αj2,.., αjk Этот вариант ничем не отличается от предыдущего случая. Во втором варианте для собственного числа rj кратности k имеется меньше чем k линейно независимых собственных векторов. Имеется два способа получения совокупности n линейно независимых решений однородной системы линейных дифференциальных уравнений. Первый основан на приведении матрицы к жордановой форме и изложен в [9,10]. Второй называется методом Эйлера и заключается в том, что для собственного числа rj соответствующие решения находятся в виде y=Pk-1(t)erjt где Pk-1(t) - вектор-функция, каждая координата которой есть полином степени не выше k-1 с неопределёнными коэффициентами, подлежащими определению. Подставляя это решение в (5.45), получаем соотношения для определения коэффициентов вектор-функции Pk-1(t).
Примеры.
1. Для линейной системы дифференциальных уравнений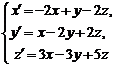 
матрица 
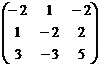имеет собственные числа λ1=3 с соответствующим собственным вектором p1=(-1,1,3)T
и λ2,3=-1 кратности 2 с собственными векторами p2=(1,1,0)Tи p3=(2,0,-1)T. Поэтому фундаментальная система решений состоит из функций p1e3t, p2e-t, p3e-t, а общее решение имеет вид
.
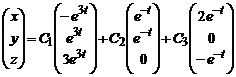2. Для системы дифференциальных уравнений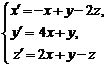 
матрица 
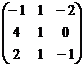имеет собственные числа λ1=3 с соответствующим собственным вектором p1=(0,2,1)Tи λ2,3=-1 кратности 2, которому соответствует только один собственный вектор p2 = (-1,2,1)T. Поэтому линейно независимые решения, соответствующие собственному числу λ2,3=-1, ищем в виде
.
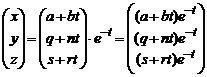Подставляя эти соотношения в исходную систему и приводя подобные, получаем систему алгебраических уравнений
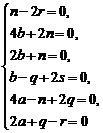
для нахождения чисел a,b,q,n,s,r. Решая эту систему, имеем b=-r,q=-2a, n=2r, s=r-a. Придавая свободным неизвестным значения a=C2, r=C3 получаем общее решение исходной системы дифференциальных уравнений
.
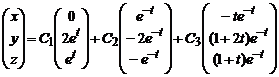