Экстремумы функции
С помощью данного сервиса можно найти наибольшее и наименьшее значение функции одной переменной f(x) с оформлением решения в Word. Если же задана функция f(x,y), следовательно, необходимо найти экстремум функции двух переменных. Также можно найти интервалы возрастания и убывания функции.
Асимптоты функции
Уравнение касательной к графику функции
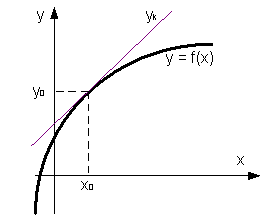
Построение графика функции методом дифференциального исчисления
Экстремум функции двух переменных
Вычисление пределов
Необходимое условие экстремума функции одной переменной
Уравнение f'0(x*) = 0 - это необходимое условие экстремума функции одной переменной, т.е. в точке x* первая производная функции должна обращаться в нуль. Оно выделяет стационарные точки xс, в которых функция не возрастает и не убывает.Достаточное условие экстремума функции одной переменной
Пусть f0(x) дважды дифференцируемая по x, принадлежащему множеству D. Если в точке x* выполняется условие:f''0(x*) > 0
Если в точке x* выполняется условие:
f''0(x*) < 0
Пример №1. Найти наибольшее и наименьшее значения функции:
на отрезке [1; 3].
Решение.
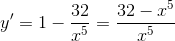
Критическая точка одна x1 = 2 (f’(x)=0). Эта точка принадлежит отрезку [1;3]. (Точка x=0 не является критической, так как 0∉[1;3]).
Вычисляем значения функции на концах отрезка и в критической точке.
f(1)=9, f(2)=5/2, f(3)=3 8/81
Ответ: fmin=5/2 при x=2; fmax=9 при x=1
Пример №2. С помощью производных высших порядков найти экстремум функции y=x-2sin(x).
Решение.
Находим производную функции: y’=1-2cos(x). Найдем критические точки: 1-cos(x)=2, cos(x)=½, x=±π/3+2πk, k∈Z. Находим y’’=2sin(x), вычисляем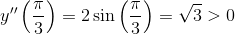 
, значит x=π/3+2πk, k∈Z – точки минимума функции; 
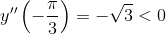, значит x=-π/3+2πk, k∈Z – точки максимума функции.
Пример №3. Исследовать на экстремум фцнкцию в окрестностях точки x=0.
Решение. Здесь необходимо найти экстремумы функции. Если экстремум x=0, то выяснить его тип (минимум или максимум). Если среди найденных точек нет x = 0, то вычислить значение функции f(x=0).
Следует обратить внимание, что когда производная с каждой стороны от данной точки не меняет своего знака, не исчерпываются возможные ситуации даже для дифференцируемых функций: может случиться, что для сколь угодно малой окрестности по одну из сторон от точки x0 или по обе стороны производная меняет знак. В этих точках приходится применять другие методы для исследования функций на экстремум.
Пример №4. Разбить число 49 на два слагаемых, произведение которых будет наибольшим.
Решение. Обозначим x - первое слагаемое. Тогда (49-x) - второе слагаемое.
Произведение будет максимальным: x·(49-x) → max
или
49x - x2
Наибольший объем цилиндра
Найти размеры цилиндра наибольшего объема, изготовленного из заготовки в форме шара радиуса R.Решение:
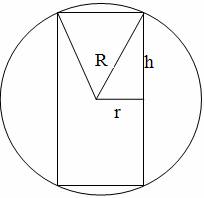
Объем цилиндра равен: V = πr2H
где H = 2h,
Подставим эти значения в целевую функцию.
V → max
Найдем экстремум функции. Поскольку функция объема V(h) зависит только от одной переменной, то найдем производную с помощью сервиса
Производная онлайни приравняем ее к нулю.
dV/dh = 2πR2 - 6πh2
dV/dh = 0
2πR2 - 6πh2 = 0 или R2 = 3h2
Откуда
При высоте
и радиусе основания 
размеры цилиндра будут наибольшими.
