Решение задачи безусловной оптимизации
Пусть решается задача поиска экстремума нелинейной функции fна всем пространстве n-мерных векторов Rn. Обозначим ▽f(x)=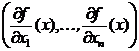
— градиент функции f в точке х = (х1,…, хn). Он задает направление скорейшего роста функции в этой точке. Точка, в которой градиент функции f равен нулю, т.е. 
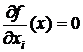для всех i=1,n,называется стационарной или критической.
Необходимое условие экстремума в задаче без ограничений дает следующая теорема
Теорема 2 (необходимое условие локального экстремума). Пусть x* — точка локального экстремума дифференцируемой функции f. Тогда x* является ее стационарной точкой.
Однако стационарная точка не всегда является точкой экстремума функции. Например, х = 0 — стационарная точка функции z = х3, но в ней она не достигает ни минимума, ни максимума. Это точка перегиба функции.
Другим примером может служить функция z=x2-y2. Точка (0, 0) является ее стационарной точкой, но в ней функция достигает минимума по переменной x и максимума по переменной y. Поэтому эта точка является не точкой экстремума, а седловой точкой этой функции.
Таким образом, стационарная точка x* будет точкой экстремума лишь при выполнении дополнительных условий, которые дает следующая теорема.
Теорема 3 (достаточные условия локального экстремума). Пусть f — дважды непрерывно дифференцируемая функция и х* — ее стационарная точка, т.е.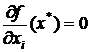 
для всех i=1,n. Тогда
1) если все главные миноры гессиана функции f в этой точке положительны, то х* — точка локального минимума;
2) если все главные миноры нечетного порядка гессиана функции f в этой точке отрицательны, а все главные миноры четного порядка положительны, то х* — точка локального максимума.
Для функции одной переменной (n = 1) условия теоремы 3 выглядят так.
Пусть х* — стационарная точка дважды непрерывно дифференцируемой функции f, т.е. 
= 0 . Тогда
1) если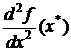 
> 0, то х* — точка локального минимума функции f;
2) если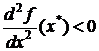 
, то х* — точка локального максимума функции f.
Для случая n = 2 условия теоремы 3 приобретают такой вид.
Пусть х* = (x*1, x*2) — стационарная точка дважды непрерывно дифференцируемой функции f, т.е.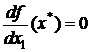 
, 
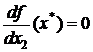, а также выполнено условие
.
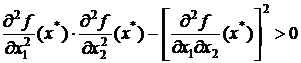Тогда х* — точка локального экстремума функции f, причем
1) если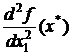 
> 0, то х* — точка локального минимума,
2) если 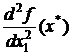< 0, то х* — точка локального максимума.
Для выпуклой (вогнутой) функции необходимое условие оптимума является достаточным.
Теорема 4. Пусть х* — стационарная точка дифференцируемой функции f. Тогда, если f — выпуклая функция, то х* — точка ее глобального минимума, а если f — вогнутая функция, то х* — точка ее глобального максимума.
Для нахождения глобального минимума (максимума) функции n переменныхf нужно выполнить следующие действия:
1. Найти все стационарные точки целевой функции f. Для этого необходимо решить систему уравнений вида
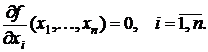(7)
2. Проверить выполнение достаточных условий минимума (максимума) во всех найденных точках.
3. Вычислить во всех найденных точках локального минимума (максимума) значение ЦФ и сравнить их между собой. Точка, в которой функция имеет наименьшее (наибольшее) значение является точкой ее глобального минимума (максимума).
Если же нужно найти минимум выпуклой (максимум вогнутой) функции, то задача существенно упрощается. Достаточно найти любую стационарную точку этой функции. Она и будет точкой ее глобального оптимума.