Системы случайных величин
Упорядоченная пара (X,Y) случайных величин X и Y называется двумерной случайной величиной, или случайным вектором двумерного пространства. Двумерная случайная величина (X,Y) называется также системой случайных величина X и Y. Множество всех возможных значений дискретной случайной величины с их вероятностями называется законом распределения этой случайной величины. Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения:P(X=xi, Y=yj) = pij, i=1,2...,n, j=1,2...,m
Назначение сервиса. С помощью сервиса по заданному закону распределения можно найти:
- ряды распределения X и Y, математическое ожидание M[X], M[Y], дисперсию D[X], D[Y];
- ковариацию cov(x,y), коэффициент корреляции rx,y, условный ряд распределения X, условное математическое ожидание M[X/Y=yi];
Инструкция. Укажите размерность матрицы распределения вероятностей (количество строк и столбцов) и ее вид. Полученное решение сохраняется в файле Word.
Пример №1. Двумерная дискретная случайная величина имеет таблицу распределения:
| Y/X | 1 | 2 | 3 | 4 |
| 10 | 0 | 0,11 | 0,12 | 0,03 |
| 20 | 0 | 0,13 | 0,09 | 0,02 |
| 30 | 0,02 | 0,11 | 0,08 | 0,01 |
| 40 | 0,03 | 0,11 | 0,05 | q |
Решение. Величину q найдем из условия Σpij = 1
Σpij = 0,02 + 0,03 + 0,11 + … + 0,03 + 0,02 + 0,01 + q = 1
0.91+q = 1. Откуда q = 0.09
Находим ряды распределения X и Y.
Пользуясь формулой ∑P(xi,yj) = pi (j=1..n), находим ряд распределения X.
| X | 10 | 20 | 30 | 40 | |
| P | 0.26 | 0.24 | 0.22 | 0.28 | ∑Pi = 1 |
Дисперсия D[X] = 102*0.26 + 202*0.24 + 302*0.22 + 402*0.28 - 25.22 = 132.96
Среднее квадратическое отклонение σ(x) = sqrt(D[X]) = sqrt(132.96) = 11.531
Пользуясь формулой ∑P(xi,yj) = qj (i=1..m), находим ряд распределения Y.
| Y | 1 | 2 | 3 | 4 | |
| P | 0.05 | 0.46 | 0.34 | 0.15 | ∑Pi = 1 |
M[y] = 1*0.05 + 2*0.46 + 3*0.34 + 4*0.15 = 2.59
Дисперсия D[Y] = 12*0.05 + 22*0.46 + 32*0.34 + 42*0.15 - 2.592 = 0.64
Среднее квадратическое отклонение σ(y) = sqrt(D[Y]) = sqrt(0.64) = 0.801
Ковариация cov(X,Y) = M[X·Y] - M[X]·M[Y] = 2·10·0.11 + 3·10·0.12 + 4·10·0.03 + 2·20·0.13 + 3·20·0.09 + 4·20·0.02 + 1·30·0.02 + 2·30·0.11 + 3·30·0.08 + 4·30·0.01 + 1·40·0.03 + 2·40·0.11 + 3·40·0.05 + 4·40·0.09 - 25.2 · 2.59 = -0.068
Коэффициент корреляции rxy = cov(x,y)/σ(x)&sigma(y) = -0.068/(11.531*0.801) = -0.00736
Пример 2. Данные статистической обработки сведений относительно двух показателей X и Y отражены в корреляционной таблице. Требуется:
- написать ряды распределения для X и Y и вычислить для них выборочные средние и выборочные средние квадратические отклонения;
- написать условные ряды распределения Y/x и вычислить условные средние Y/x;
- изобразить графически зависимость условных средних Y/x от значений X;
- рассчитать выборочный коэффициент корреляции Y на X;
- написать выборочное уравнение прямой регрессии;
- изобразить геометрически данные корреляционной таблицы и построить прямую регрессии.
Множество всех возможных значений дискретной случайной величины с их вероятностями называется законом распределения этой случайной величины.
Дискретная двумерная случайная величина (X,Y) считается заданной, если известен ее закон распределения:
P(X=xi, Y=yj) = pij, i=1,2...,n, j=1,2..,m
| X / Y | 20 | 30 | 40 | 50 | 60 |
| 11 | 2 | 0 | 0 | 0 | 0 |
| 16 | 4 | 6 | 0 | 0 | 0 |
| 21 | 0 | 3 | 6 | 2 | 0 |
| 26 | 0 | 0 | 45 | 8 | 4 |
| 31 | 0 | 0 | 4 | 6 | 7 |
| 36 | 0 | 0 | 0 | 0 | 3 |
1. Зависимость случайных величин X и Y.
Находим ряды распределения X и Y.
Пользуясь формулой ∑P(xi,yj) = pi (j=1..n), находим ряд распределения X.
| X | 11 | 16 | 21 | 26 | 31 | 36 | |
| P | 2 | 10 | 11 | 57 | 17 | 3 | ∑Pi = 100 |
M[x] = (11*2 + 16*10 + 21*11 + 26*57 + 31*17 + 36*3 )/100 = 25.3
Дисперсия D[X].
D[X] = (112*2 + 162*10 + 212*11 + 262*57 + 312*17 + 362*3 )/100 - 25.32 = 24.01
Среднее квадратическое отклонение σ(x).
Пользуясь формулой ∑P(xi,yj) = qj (i=1..m), находим ряд распределения Y.
| Y | 20 | 30 | 40 | 50 | 60 | |
| P | 6 | 9 | 55 | 16 | 14 | ∑Pi = 100 |
M[y] = (20*6 + 30*9 + 40*55 + 50*16 + 60*14 )/100 = 42.3
Дисперсия D[Y].
D[Y] = (202*6 + 302*9 + 402*55 + 502*16 + 602*14 )/100 - 42.32 = 99.71
Среднее квадратическое отклонение σ(y).
Поскольку, P(X=11,Y=20) = 2≠2·6, то случайные величины X и Y зависимы.
2. Условный закон распределения X.
Условный закон распределения X(Y=20).
P(X=11/Y=20) = 2/6 = 0.33
P(X=16/Y=20) = 4/6 = 0.67
P(X=21/Y=20) = 0/6 = 0
P(X=26/Y=20) = 0/6 = 0
P(X=31/Y=20) = 0/6 = 0
P(X=36/Y=20) = 0/6 = 0
Условное математическое ожидание M[X/Y=20).
M[X/Y=y] = 11*0.33 + 16*0.67 + 21*0 + 26*0 + 31*0 + 36*0 = 14.33
Условная дисперсия D[X/Y=20).
D[X/Y=y] = 112*0.33 + 162*0.67 + 212*0 + 262*0 + 312*0 + 362*0 - 14.332 = 5.56
Условный закон распределения X(Y=30).
P(X=11/Y=30) = 0/9 = 0
P(X=16/Y=30) = 6/9 = 0.67
P(X=21/Y=30) = 3/9 = 0.33
P(X=26/Y=30) = 0/9 = 0
P(X=31/Y=30) = 0/9 = 0
P(X=36/Y=30) = 0/9 = 0
Условное математическое ожидание M[X/Y=30).
M[X/Y=y] = 11*0 + 16*0.67 + 21*0.33 + 26*0 + 31*0 + 36*0 = 17.67
Условная дисперсия D[X/Y=30).
D[X/Y=y] = 112*0 + 162*0.67 + 212*0.33 + 262*0 + 312*0 + 362*0 - 17.672 = 5.56
Условный закон распределения X(Y=40).
P(X=11/Y=40) = 0/55 = 0
P(X=16/Y=40) = 0/55 = 0
P(X=21/Y=40) = 6/55 = 0.11
P(X=26/Y=40) = 45/55 = 0.82
P(X=31/Y=40) = 4/55 = 0.0727
P(X=36/Y=40) = 0/55 = 0
Условное математическое ожидание M[X/Y=40).
M[X/Y=y] = 11*0 + 16*0 + 21*0.11 + 26*0.82 + 31*0.0727 + 36*0 = 25.82
Условная дисперсия D[X/Y=40).
D[X/Y=y] = 112*0 + 162*0 + 212*0.11 + 262*0.82 + 312*0.0727 + 362*0 - 25.822 = 4.51
Условный закон распределения X(Y=50).
P(X=11/Y=50) = 0/16 = 0
P(X=16/Y=50) = 0/16 = 0
P(X=21/Y=50) = 2/16 = 0.13
P(X=26/Y=50) = 8/16 = 0.5
P(X=31/Y=50) = 6/16 = 0.38
P(X=36/Y=50) = 0/16 = 0
Условное математическое ожидание M[X/Y=50).
M[X/Y=y] = 11*0 + 16*0 + 21*0.13 + 26*0.5 + 31*0.38 + 36*0 = 27.25
Условная дисперсия D[X/Y=50).
D[X/Y=y] = 112*0 + 162*0 + 212*0.13 + 262*0.5 + 312*0.38 + 362*0 - 27.252 = 10.94
Условный закон распределения X(Y=60).
P(X=11/Y=60) = 0/14 = 0
P(X=16/Y=60) = 0/14 = 0
P(X=21/Y=60) = 0/14 = 0
P(X=26/Y=60) = 4/14 = 0.29
P(X=31/Y=60) = 7/14 = 0.5
P(X=36/Y=60) = 3/14 = 0.21
Условное математическое ожидание M[X/Y=60).
M[X/Y=y] = 11*0 + 16*0 + 21*0 + 26*0.29 + 31*0.5 + 36*0.21 = 30.64
Условная дисперсия D[X/Y=60).
D[X/Y=y] = 112*0 + 162*0 + 212*0 + 262*0.29 + 312*0.5 + 362*0.21 - 30.642 = 12.37
3. Условный закон распределения Y.
Условный закон распределения Y(X=11).
P(Y=20/X=11) = 2/2 = 1
P(Y=30/X=11) = 0/2 = 0
P(Y=40/X=11) = 0/2 = 0
P(Y=50/X=11) = 0/2 = 0
P(Y=60/X=11) = 0/2 = 0
Условное математическое ожидание M[Y/X=11).
M[Y/X=x] = 20*1 + 30*0 + 40*0 + 50*0 + 60*0 = 20
Условная дисперсия D[Y/X=11).
D[Y/X=x] = 202*1 + 302*0 + 402*0 + 502*0 + 602*0 - 202 = 0
Условный закон распределения Y(X=16).
P(Y=20/X=16) = 4/10 = 0.4
P(Y=30/X=16) = 6/10 = 0.6
P(Y=40/X=16) = 0/10 = 0
P(Y=50/X=16) = 0/10 = 0
P(Y=60/X=16) = 0/10 = 0
Условное математическое ожидание M[Y/X=16).
M[Y/X=x] = 20*0.4 + 30*0.6 + 40*0 + 50*0 + 60*0 = 26
Условная дисперсия D[Y/X=16).
D[Y/X=x] = 202*0.4 + 302*0.6 + 402*0 + 502*0 + 602*0 - 262 = 24
Условный закон распределения Y(X=21).
P(Y=20/X=21) = 0/11 = 0
P(Y=30/X=21) = 3/11 = 0.27
P(Y=40/X=21) = 6/11 = 0.55
P(Y=50/X=21) = 2/11 = 0.18
P(Y=60/X=21) = 0/11 = 0
Условное математическое ожидание M[Y/X=21).
M[Y/X=x] = 20*0 + 30*0.27 + 40*0.55 + 50*0.18 + 60*0 = 39.09
Условная дисперсия D[Y/X=21).
D[Y/X=x] = 202*0 + 302*0.27 + 402*0.55 + 502*0.18 + 602*0 - 39.092 = 44.63
Условный закон распределения Y(X=26).
P(Y=20/X=26) = 0/57 = 0
P(Y=30/X=26) = 0/57 = 0
P(Y=40/X=26) = 45/57 = 0.79
P(Y=50/X=26) = 8/57 = 0.14
P(Y=60/X=26) = 4/57 = 0.0702
Условное математическое ожидание M[Y/X=26).
M[Y/X=x] = 20*0 + 30*0 + 40*0.79 + 50*0.14 + 60*0.0702 = 42.81
Условная дисперсия D[Y/X=26).
D[Y/X=x] = 202*0 + 302*0 + 402*0.79 + 502*0.14 + 602*0.0702 - 42.812 = 34.23
Условный закон распределения Y(X=31).
P(Y=20/X=31) = 0/17 = 0
P(Y=30/X=31) = 0/17 = 0
P(Y=40/X=31) = 4/17 = 0.24
P(Y=50/X=31) = 6/17 = 0.35
P(Y=60/X=31) = 7/17 = 0.41
Условное математическое ожидание M[Y/X=31).
M[Y/X=x] = 20*0 + 30*0 + 40*0.24 + 50*0.35 + 60*0.41 = 51.76
Условная дисперсия D[Y/X=31).
D[Y/X=x] = 202*0 + 302*0 + 402*0.24 + 502*0.35 + 602*0.41 - 51.762 = 61.59
Условный закон распределения Y(X=36).
P(Y=20/X=36) = 0/3 = 0
P(Y=30/X=36) = 0/3 = 0
P(Y=40/X=36) = 0/3 = 0
P(Y=50/X=36) = 0/3 = 0
P(Y=60/X=36) = 3/3 = 1
Условное математическое ожидание M[Y/X=36).
M[Y/X=x] = 20*0 + 30*0 + 40*0 + 50*0 + 60*1 = 60
Условная дисперсия D[Y/X=36).
D[Y/X=x] = 202*0 + 302*0 + 402*0 + 502*0 + 602*1 - 602 = 0
Ковариация.
cov(X,Y) = M[X·Y] - M[X]·M[Y]
cov(X,Y) = (20·11·2 + 20·16·4 + 30·16·6 + 30·21·3 + 40·21·6 + 50·21·2 + 40·26·45 + 50·26·8 + 60·26·4 + 40·31·4 + 50·31·6 + 60·31·7 + 60·36·3)/100 - 25.3 · 42.3 = 38.11
Если случайные величины независимы, то их ковариации равна нулю. В нашем случае cov(X,Y) ≠ 0.
Коэффициент корреляции.
Уравнение линейной регрессии с y на x имеет вид:
Уравнение линейной регрессии с x на y имеет вид:
Найдем необходимые числовые характеристики.
Выборочные средние:
x = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 42.3
y = (20(2 + 4) + 30(6 + 3) + 40(6 + 45 + 4) + 50(2 + 8 + 6) + 60(4 + 7 + 3))/100 = 25.3
Дисперсии:
σ2x = (202(2 + 4) + 302(6 + 3) + 402(6 + 45 + 4) + 502(2 + 8 + 6) + 602(4 + 7 + 3))/100 - 42.32 = 99.71
σ2y = (112(2) + 162(4 + 6) + 212(3 + 6 + 2) + 262(45 + 8 + 4) + 312(4 + 6 + 7) + 362(3))/100 - 25.32 = 24.01
Откуда получаем среднеквадратические отклонения:
σx = 9.99 и σy = 4.9
и ковариация:
Cov(x,y) = (20·11·2 + 20·16·4 + 30·16·6 + 30·21·3 + 40·21·6 + 50·21·2 + 40·26·45 + 50·26·8 + 60·26·4 + 40·31·4 + 50·31·6 + 60·31·7 + 60·36·3)/100 - 42.3 · 25.3 = 38.11
Определим коэффициент корреляции:
Запишем уравнения линий регрессии y(x):
и вычисляя, получаем:
yx = 0.38 x + 9.14
Запишем уравнения линий регрессии x(y):
и вычисляя, получаем:
xy = 1.59 y + 2.15
Если построить точки, определяемые таблицей и линии регрессии, увидим, что обе линии проходят через точку с координатами (42.3; 25.3) и точки расположены близко к линиям регрессии.
Значимость коэффициента корреляции.
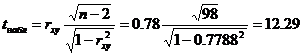
По таблице Стьюдента с уровнем значимости α=0.05 и степенями свободы k=100-m-1 = 98 находим tкрит:
tкрит (n-m-1;α/2) = (98;0.025) = 1.984
где m = 1 - количество объясняющих переменных.
Если tнабл > tкритич, то полученное значение коэффициента корреляции признается значимым (нулевая гипотеза, утверждающая равенство нулю коэффициента корреляции, отвергается).
Поскольку tнабл > tкрит, то отклоняем гипотезу о равенстве 0 коэффициента корреляции. Другими словами, коэффициент корреляции статистически - значим.
Задание. Количество попаданий пар значений случайных величин X и Y в соответствующие интервалы приведены в таблице. По этим данным найти выборочный коэффициент корреляции и выборочные уравнения прямых линий регрессии Y на X и X на Y.
Решение
Пример. Распределение вероятностей двумерной случайной величины (X, Y) задано таблицей. Найти законы распределения составляющих величин X, Y и коэффициент корреляции p(X, Y).
Скачать решение
Задание. Двумерная дискретная величина (X, Y) задана законом распределения. Найти законы распределения составляющих X и Y, ковариацию и коэффициент корреляции.