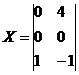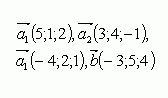Решение матричных уравнений
Назначение сервиса. Матричный калькулятор предназначен для решения систем линейных уравнений матричным способом (см. пример решения подобных задач).A·X - B = C, то необходимо, сначала сложить матрицы C + B, и находить решение для выражения A·X = D, где D = C + B. Если задано выражение A*X = B2, то предварительно матрицу B надо возвести в квадрат.
По координатам вершин треугольника найти площадь, уравнения сторон, уравнение медианы, уравнение биссектрисы
Координаты вектора в базисе
По координатам вершин пирамиды найти
Построение графика функции методом дифференциального исчисления

Экстремум функции двух переменных
Вычисление пределов
Вычисление интегралов
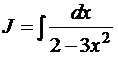
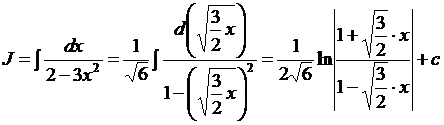
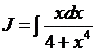
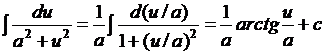
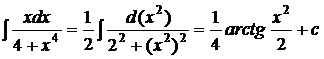
Пример №1. Задание. Найти решение матричного уравнения ![]()
Решение. Обозначим:
![]()
![]()
![]()
Тогда матричное уравнение запишется в виде: A·X·B = C.
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1:Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1·A·X·B·B-1 = A-1·C·B-1. Так как A·A-1 = B·B-1 = E и E·X = X·E = X, то X = A-1·C·B-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT: ![]()
Обратная матрица A-1: ![]()
Найдем обратную матрицу B-1.
Транспонированная матрица BT: ![]()
Обратная матрица
| B-1 = -½ |
|
Матрицу X ищем по формуле: X = A-1·C·B-1
| X = - |
| * |
| -½ |
| = |
|
Ответ:
| X = |
|
Пример №2. Задание. Решить матричное уравнение ![]()
Решение. Обозначим: ![]()
![]()
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=0
Так как A вырожденная матрица (определитель равен 0), следовательно уравнение решения не имеет.
Пример №3. Задание. Найти решение матричного уравнения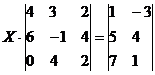
Решение. Обозначим: 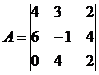
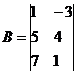
Тогда матричное уравнение запишется в виде: X·A = B.
Определитель матрицы А равен detA=-60
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT: 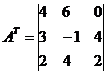
Обратная матрица A-1: 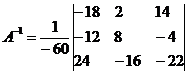
Матрицу X ищем по формуле: X = B·A-1
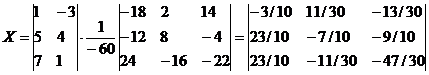
Ответ:
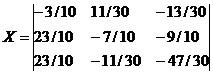
Пример №4. Задание. Решить матричное уравнение 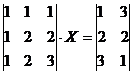
Решение. Обозначим: 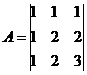
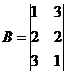
Тогда матричное уравнение запишется в виде: A·X = B.
Определитель матрицы А равен detA=1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Найдем обратную матрицу A-1.
Транспонированная матрица AT: 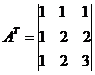
Обратная матрица A-1: 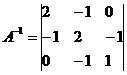
Матрицу Х ищем по формуле: X = A-1·B
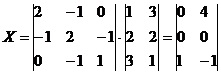
Ответ: