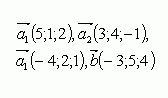Как найти координаты вектора в базисе
Доказать, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.Пусть в R3 относительно канонического базисы даны четыре вектора f1 = (1,2,3), f2 = (2,3,7), f3=(1,3,1), x = (2,3,4). Докажите, что векторы f1, f2, f3 можно принять за новый базис. Найдите координаты η1, η2, η3 вектора х относительно этого базиса.
Решение:
Записываем матрицу перехода А:
и находим ее определитель
<>0
Видим, что ранг матрицы С равен трем. Из теоремы о базисном миноре векторы f1, f2, f3 линейно независимы, а поэтому могут быть приняты в качестве базиса пространства R3.
Находим обратную матрицу А-1.
Транспонированная матрица:
Алгебраические дополнения:
Обратная матрица А-1
Находим координаты вектора х относительно нового базиса.
Перейти к онлайн решению своей задачи
Пример №1. Даны векторы a{1;2;1}, b{2;-2;1}, c{1;-2;0} и d {0;3;1}. Установить, что векторы a, b, c образуют базис, и найти координаты вектора d в этом базисе.
Решение:
Соотношение, записанное для векторов d = αa + βb + γc, справедливо для каждой из проекций:
α*1 + β*2 + γ*1 = 0
α*2 - β*2 - γ*2 = 3
α*1 + β*1 + γ0 = 1
т.е. получена алгебраическая система трёх уравнений с тремя неизвестными. Решение системы удобнее вычислять методом Крамера или методом обратной матрицы:
α = 1/2; β = 1/2; γ = -3/2
следовательно, и вектор d имеет разложение в базисе a, b, c:
d = 1/2a + 1/2b - 3/2c
Пример №2. Даны векторы ![]() . Показать, что векторы
. Показать, что векторы ![]() образуют базис трехмерного пространства и найти координаты вектора
образуют базис трехмерного пространства и найти координаты вектора ![]() в этом базисе:
в этом базисе:
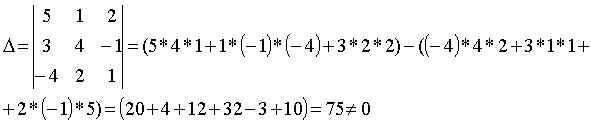
Запишем данное равенство в координатной форме:
(-3;5;4)=α(5;1;2) + β(3;4;-1) + γ(-4;2;1)
Используя свойства векторов, получим следующее равенство:
(-3;5;4) = (5α;α;2α) + (3β;4β;-β) + (-4γ;2γ;γ)
(-3;5;4) = (5α+3β-4γ;α+4β+2γ;2α-β+γ)
По свойству равенства векторов имеем:
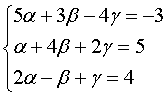
Решая полученную систему уравнений методом Гаусса (методом последовательного исключения неизвестных из уравнений системы), выберем в качестве ведущего уравнения второе уравнение системы:
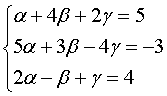
Выразим из первого уравнения полученной системы α и подставим полученное выражение во второе и третье уравнения системы:
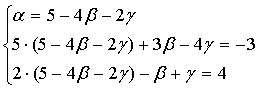
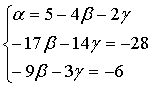
Разделим второе уравнение системы на -1 ,а третье уравнение системы на -3 и выразим из полученного равенства γ :
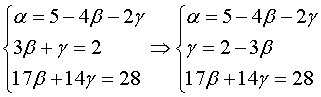
Подставим полученное выражение для γ в третье уравнение системы:
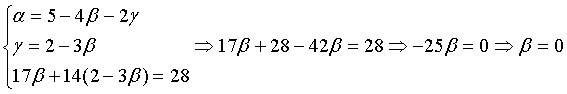
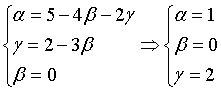
В итоге получим разложение вектора
Ответ:
Пример №3. Даны два линейных преобразования:
х'1 = a11x1 + a12x2 + a13x3, х''1 = b11x'1 + b12x'2 + b13x'3,
х'2 = a21x1 + a22x2 + a23x3, х''2 = b21x'1 + b22x'2 + b23x'3,
х'3 = a31x1 + a32x2 + a33x3, х''3 = b31x'1 + b32x'2 + b33x'3,
Средствами матричного исчисления найти преобразование, выражающее х''1, x''2, x''3 через х1, х2, х3.
х'1 = 4x1 + 3x2 + 5x3, х''1 = - x'1 + 3x'2 - 2x'3,
х'2 = 6x1 + 7x2 + x3, х''2 = - 4x'1 + x'2 + 2x'3,
х'3 = 9x1 + x2 + 8x3, х''3 = 3x'1 - 4x'2 + 5x'3,
Решение. Используя калькулятор, получаем:
Обозначим:
| A = |
|
| B = |
|
Вычислим определитель матрицы А:
∆ = 4*(7*8 - 1*1) - 6*(3*8 - 1*5) + 9*(3*1 - 7*5) = -182
Определитель матрицы А равен detA=-182
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Найдем обратную матрицу A-1.
| A-1 = -1/182 |
|
Матрицу Х ищем по формуле:
| X = A-1·B = -1/182 |
| * |
| = |
|
x'1 = 75/182x1 -146/91x2 + 19/13
x'2 = -13/14x1 + 12/7 -x3
x'3 = 5/182x1 + 13/91x2 -12/13x3
Пример №4. В декартовой прямой системе координат даны вершины пирамиды A(3,0,-1), B(-1,-2,-4), C(-1,2,4), D(7,-3,1). Найдите:
а) длину ребра AB;
б) косинус угла между векторами AB и AC;
в) уравнение ребра AB;
г) уравнение грани ABC;
д) уравнение высоты, опущенной из вершины D на грань ABC;
е) координаты векторов e1=AB, e2=AC, e3=AD и докажите, что они образуют линейную независимую систему;
ж) координаты вектора MN, где M и N – середины ребер AD и DC соответственно;
з) разложение вектора MN по базису (e1, e2, e3)
Решение. Пункты (а-д) решаются через онлайн калькулятор.
Задание 1. Разложить вектор d=(8;-5) по векторам a=(1;-2) и b=(2;3).
Решение. Векторы a и b образуют базис на плоскости, так как они не коллинеарны (![]() , то есть соответствующие координаты этих векторов не пропорциональны).
, то есть соответствующие координаты этих векторов не пропорциональны).
Следовательно, вектор d = αa+βb, где α и β – коэффициенты, которые надо найти.
Таким образом, имеем равенство
8i-5j=α(i-2j)+β(2i+3j)=(α+2β)i+ (-2α+3β)j.
В координатной форме это равенство примет вид ![]()
![]()
Решим полученную систему уравнений.
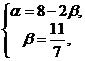
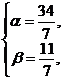
Перейти к онлайн решению своей задачи
Пример №2. Разложите вектор v = (36; -6) по базису e1=(-5;3),e2=(-2;-4).
Решение. Даны векторы ε1(-5;3), ε2(-2;-4), X(36;-6). Показать, что векторы образуют базис двухмерного пространства и найти координаты вектора X в этом базисе.
Данная задача состоит из двух частей. Сначала необходимо проверить образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
| E = |
|
∆ = (-5)*(-4) - (-2)*3 = 26
Определитель матрицы равен ∆ =26
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1, α2, что имеет место равенство:
X = α1ε1 + α2ε2
Запишем данное равенство в координатной форме:
(36;-6) = α(-5;3) + α(-2;-4)
Используя свойства векторов, получим следующее равенство:
(36;-6) = (-5α1;3α1;) + (-2α2;-4α2;)
(36;-6) = (-5α1 -2α2;3α1 -4α2)
По свойству равенства векторов имеем:
-5α1 -2α2 = 36
3α1 -4α2 = -6
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
| X = |
|
X = -6ε1 -3ε2