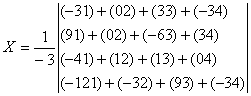Решение СЛАУ методом обратной матрицы
Назначение сервиса. С помощью данного онлайн-калькулятора вычисляются неизвестные {x1, x2, ..., xn} в системе уравнений. Решение осуществляется методом обратной матрицы. При этом:
- вычисляется определитель матрицы A;
- через алгебраические дополнения находится обратная матрица A-1;
- осуществляется создание шаблона решения в Excel;
Решение проводится непосредственно на сайте (в онлайн режиме) и является бесплатным. Результаты вычислений оформляются в отчете формата Word.
Инструкция. Для получения решения методом обратной матрицы необходимо задать размерность матрицы. Далее в новом диалоговом окне заполнить матрицу A и вектор результатов B.
Напомним, что решением системы линейных уравнений называется всякая совокупность чисел {x1, x2, ..., xn}, подстановка которых в эту систему вместо соответствующих неизвестных обращает каждое уравнение системы в тождество.
Система линейных алгебраических уравнений обычно записывается как (для 3-х переменных):
2x1-3x2+x3 = 4
-x1+2x2+5x3 = 10
3x1-x2+3x3 = -1
|
или |
2x-3y+z = 4
-z+2y+5z = 10
3x-y+3z = -1
|
См. также Решение матричных уравнений.
Алгоритм решения
- Вычисляется определитель матрицы A. Если определитель равен нулю, то конец решения. Система имеет бесконечное множество решений.
- При определителе отличном от нуля, через алгебраические дополнения находится обратная матрица A-1.
- Вектор решения X={x1, x2, ..., xn} получается умножением обратной матрицы на вектор результата B.
Пример №1. Найти решение системы матричным методом. Запишем матрицу в виде:
Вектор B:
BT = (3,-2,-1)
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆ = 2•(1•(-2)-2•0)-(-2•(3•(-2)-2•1))+1•(3•0-1•1) = -21
Итак, определитель -21 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Транспонированная матрица
Алгебраические дополнения.
| A1,1 = (-1)1+1 | | | ∆1,1 = (1•(-2)-0•2) = -2 |
| A1,2 = (-1)1+2 | | | ∆1,2 = -(3•(-2)-1•2) = 8 |
| A1,3 = (-1)1+3 | | | ∆1,3 = (3•0-1•1) = -1 |
| A2,1 = (-1)2+1 | | | ∆2,1 = -(-2•(-2)-0•1) = -4 |
| A2,2 = (-1)2+2 | | | ∆2,2 = (2•(-2)-1•1) = -5 |
| A2,3 = (-1)2+3 | | | ∆2,3 = -(2•0-1•(-2)) = -2 |
| A3,1 = (-1)3+1 | | | ∆3,1 = (-2•2-1•1) = -5 |
| A3,2 = (-1)3+2 | | | ∆3,2 = -(2•2-3•1) = -1 |
| A3,3 = (-1)3+3 | | | ∆3,3 = (2•1-3•(-2)) = 8 |
Обратная матрица:
Вектор результатов X = A-1 • B
XT = (1,0,1)
x1 = -21 / -21 = 1
x2 = 0 / -21 = 0
x3 = -21 / -21 = 1
Проверка:
2•1+3•0+1•1 = 3
-2•1+1•0+0•1 = -2
1•1+2•0+-2•1 = -1
Пример №2. Решить СЛАУ методом обратной матрицы.
2 x 1 + 3x2 + 3x3+ x4= 1
3 x 1 + 5x2 + 3x3+ 2x4= 2
5 x 1 + 7x2 + 6x3+ 2x4= 3
4 x 1 + 4x2 + 3x3+ x4= 4
Запишем матрицу в виде:

Вектор B:
BT = (1,2,3,4)
Главный определитель
Минор для (1,1):

= 5•(6•1-3•2)-7•(3•1-3•2)+4•(3•2-6•2) = -3
Минор для (2,1):

= 3•(6•1-3•2)-7•(3•1-3•1)+4•(3•2-6•1) = 0
Минор для (3,1):

= 3•(3•1-3•2)-5•(3•1-3•1)+4•(3•2-3•1) = 3
Минор для (4,1):

= 3•(3•2-6•2)-5•(3•2-6•1)+7•(3•2-3•1) = 3
Определитель минора
∆ = 2•(-3)-3•0+5•3-4•3 = -3
Транспонированная матрица

Алгебраические дополнения

∆1,1 = 5•(6•1-2•3)-3•(7•1-2•4)+2•(7•3-6•4) = -3

∆1,2 = -3•(6•1-2•3)-3•(7•1-2•4)+1•(7•3-6•4) = 0

∆1,3 = 3•(3•1-2•3)-3•(5•1-2•4)+1•(5•3-3•4) = 3

∆1,4 = -3•(3•2-2•6)-3•(5•2-2•7)+1•(5•6-3•7) = -3

∆2,1 = -3•(6•1-2•3)-3•(5•1-2•4)+2•(5•3-6•4) = 9

∆2,2 = 2•(6•1-2•3)-3•(5•1-2•4)+1•(5•3-6•4) = 0

∆2,3 = -2•(3•1-2•3)-3•(3•1-2•4)+1•(3•3-3•4) = -6

∆2,4 = 2•(3•2-2•6)-3•(3•2-2•5)+1•(3•6-3•5) = 3

∆3,1 = 3•(7•1-2•4)-5•(5•1-2•4)+2•(5•4-7•4) = -4

∆3,2 = -2•(7•1-2•4)-3•(5•1-2•4)+1•(5•4-7•4) = 1

∆3,3 = 2•(5•1-2•4)-3•(3•1-2•4)+1•(3•4-5•4) = 1

∆3,4 = -2•(5•2-2•7)-3•(3•2-2•5)+1•(3•7-5•5) = 0

∆4,1 = -3•(7•3-6•4)-5•(5•3-6•4)+3•(5•4-7•4) = -12

∆4,2 = 2•(7•3-6•4)-3•(5•3-6•4)+3•(5•4-7•4) = -3

∆4,3 = -2•(5•3-3•4)-3•(3•3-3•4)+3•(3•4-5•4) = 9

∆4,4 = 2•(5•6-3•7)-3•(3•6-3•5)+3•(3•7-5•5) = -3
Обратная матрица

Вектор результатов X
X = A-1 ∙ B
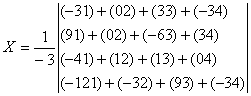

XT = (2,-1,-0.33,1)
x1 = 2; x2 = -1; x3 = -0.33; x4 = 1
Пример №3. Систему уравнений записать в матричной форме и решить ее с помощью обратной матрицы. Сделать проверку полученного решения.
Решение:xls
Пример №4. Записать систему уравнений в матричной форме и решить с помощью обратной матрицы.
Решение:xls
Пример №5. Дана система трех линейных уравнений с тремя неизвестными. Требуется: 1) найти ее решение с помощью формул Крамера; 2) записать систему в матричной форме и решить ее средствами матричного исчисления.
Методические рекомендации. После решения методом Крамера, найдите кнопку "Решение методом обратной матрицы для исходных данных". Вы получите соответствующее решение. Таким образом, данные вновь заполнять не придется.
Решение. Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:
Вектор B:
BT=(4,-3,-3)
С учетом этих обозначений данная система уравнений принимает следующую матричную форму: А*Х = B.
Если матрица А — невырожденная (ее определитель отличен от нуля, то она имеет обратную матрицу А-1. Умножив обе части уравнения на А-1, получим: А-1*А*Х = А-1*B, А-1*А=Е.
Это равенство называется матричной записью решения системы линейных уравнений. Для нахождения решения системы уравнений необходимо вычислить обратную матрицу А-1.
Система будет иметь решение, если определитель матрицы A отличен от нуля.
Найдем главный определитель.
∆=-1•(-2•(-1)-1•1)-3•(3•(-1)-1•0)+2•(3•1-(-2•0))=14
Итак, определитель 14 ≠ 0, поэтому продолжаем решение. Для этого найдем обратную матрицу через алгебраические дополнения.
Пусть имеем невырожденную матрицу А:
| A= | | a11 | a12 | a13 | | a21 | a22 | a23 | | a31 | a32 | a33 |
| | |
Тогда:
| A=1/∆ | | A11 | A21 | A31 | | A12 | A22 | A32 | | A13 | A23 | A33 |
| | |
где Aij — алгебраическое дополнение элемента aij в определителе матрицы А, которое является произведением (—1)i+j на минор (определитель) n-1 порядка, полученный вычеркиванием i-й строки и j-го столбца в определителе матрицы А.
Транспонированная матрица
Вычисляем алгебраические дополнения.
∆1,1=(-2•(-1)-1•1)=1
∆1,2=-(3•(-1)-0•1)=3
∆1,3=(3•1-0•(-2))=3
∆2,1=-(3•(-1)-1•2)=5
∆2,2=(-1•(-1)-0•2)=1
∆2,3=-(-1•1-0•3)=1
∆3,1=(3•1-(-2•2))=7
∆3,2=-(-1•1-3•2)=7
∆3,3=(-1•(-2)-3•3)=-7
Обратная матрица
Вектор результатов X
X=A-1 • B
XT=(-1,1,2)
x1=-14 / 14=-1
x2=14 / 14=1
x3=28 / 14=2
Проверка.
-1•-1+3•1+0•2=4
3•-1+-2•1+1•2=-3
2•-1+1•1+-1•2=-3
doc:xls
Ответ: -1,1,2.
Пример №6. Решить неоднородную систему линейных алгебраических уравнений методом обратной матрицы.
Запишем матрицу в виде:
Главный определитель
∆=4•(0•1-3•(-2))-2•(1•1-3•(-1))+0•(1•(-2)-0•(-1))=16
Транспонированная матрица
Алгебраические дополнения.
∆1,1=(0•1-(-2•3))=6
∆1,2=-(1•1-(-1•3))=-4
∆1,3=(1•(-2)-(-1•0))=-2
∆2,1=-(2•1-(-2•0))=-2
∆2,2=(4•1-(-1•0))=4
∆2,3=-(4•(-2)-(-1•2))=6
∆3,1=(2•3-0•0)=6
∆3,2=-(4•3-1•0)=-12
∆3,3=(4•0-1•2)=-2
Обратная матрица
| A-1= | | 0,38 | -0,25 | -0,13 | | -0,13 | 0,25 | 0,38 | | 0,38 | -0,75 | -0,13 |
| | |
Проверим правильность нахождения обратной матрицы путем умножения исходной матрицы на обратную. Должны получить единичную матрицу E.
E=A*A-1=
| (4•6)+(1•(-2))+(-1•6) | (4•(-4))+(1•4)+(-1•(-12)) | (4•(-2))+(1•6)+(-1•(-2)) |
| (2•6)+(0•(-2))+(-2•6) | (2•(-4))+(0•4)+(-2•(-12)) | (2•(-2))+(0•6)+(-2•(-2)) |
| (0•6)+(3•(-2))+(1•6) | (0•(-4))+(3•4)+(1•(-12)) | (0•(-2))+(3•6)+(1•(-2)) |
Пример №7. Решение матричных уравнений.
Обозначим:
Тогда матричное уравнение запишется в виде: Y·A = B.
Вычислим определитель матрицы А:
∆ = 3*(1*0 - 3*4) - 2*(0*0 - 3*5) + -1*(0*4 - 1*5) = -1
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT.
Алгебраические дополнения
∆1,1 = (1*0 - 4*3) = -12
∆1,2 = -(0*0 - 5*3) = 15
∆1,3 = (0*4 - 5*1) = -5
∆2,1 = -(2*0 - 4*(-1)) = -4
∆2,2 = (3*0 - 5*(-1)) = 5
∆2,3 = -(3*4 - 5*2) = -2
∆3,1 = (2*3 - 1*(-1)) = 7
∆3,2 = -(3*3 - 0*(-1)) = -9
∆3,3 = (3*1 - 0*2) = 3
Обратная матрица A-1.
Матрицу X ищем по формуле: X = B·A-1
Ответ:
Пример №8. Обозначим через А — матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:
Вектор B:
BT=(31,13,10)
Посмотреть все шаги решения
XT=(4.05,6.13,7.54)
x1=158 / 39=4.05
x2=239 / 39=6.13
x3=294 / 39=7.54
Проверка.
-2•4.05+-1•6.13+6•7.54=31
1•4.05+-1•6.13+2•7.54=13
2•4.05+4•6.13+-3•7.54=10
Пример №9. Обозначим через А - матрицу коэффициентов при неизвестных; X — матрицу-столбец неизвестных; B - матрицу-столбец свободных членов:
Вектор B:
BT=(31,13,10)
Посмотреть всё решение
XT=(5.21,4.51,6.15)
x1=276 / 53=5.21
x2=239 / 53=4.51
x3=326 / 53=6.15
Проверка.
-2•5.21+1•4.51+6•6.15=31
1•5.21+-1•4.51+2•6.15=13
2•5.21+4•4.51+-3•6.15=10
Пример №10. Решение матричных уравнений.
Обозначим:
Тогда матричное уравнение запишется в виде: Y·A = B.
Вычислим определитель матрицы А:
∆ = 2*(-3) - 1*3 = -9
Определитель матрицы А равен detA=-9
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT.
Алгебраические дополнения
A11 = (-1)1+1·-3 = -3; A12 = (-1)1+2·3 = -3; A21 = (-1)2+1·1 = -1; A22 = (-1)2+2·2 = 2;
Обратная матрица A-1.
Матрицу X ищем по формуле: X = B·A-1
Ответ: