Решение матричных уравнений
Предварительно рекомендуется изучить основные действия над матрицами.Даны матричные уравнения
A·X = B, (1)
Y·A = B, (2)
где A и B – заданные матрицы, причем A – невырожденная. Требуется найти матрицы X и Y.
Y·A = B, (2)
Нельзя ли определить деление матриц?
Вспомним, что в числовой области частное от деления b на a определяется как решение уравнения a∙x=b (или x∙a=b) и существует не всегда. Можно попытаться определить «деление» матриц, рассматривая уравнения (1) и (2), в которых, согласно правилу умножения, матрицы A, B, X, Y не могут иметь произвольную структуру. Так, в первом уравнении матрицы A и B должны иметь одинаковое число строк, а во втором – одинаковое число столбцов. Уже отсюда ясно, что если даже оба эти уравнения однозначно разрешимы (а это далеко не всегда так), то их решения вполне могут быть матрицами не только разными, но и разной структуры. Таким образом, для матриц оказывается невозможным определить деление с привычными свойствами.
Матричные уравнения вида (1) и (2) решаются следующим образом. Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения (1) на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или
X = A-1·B. (3)
Аналогично, умножая справа обе части равенства (2) на A-1, будем иметь: Y·A· A-1 = B· A-1, откуда находим, что
Y = B· A-1. (4)
Пример 1. Решить матричное уравнение
.
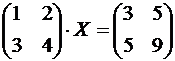Решение. Обозначим
, 
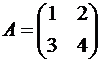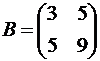. Тогда матричное уравнение запишется в виде A·X = B. Найдем A-1: 
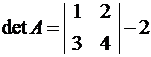; A11 = 4; A21 = -3; A12 = -2; A22 = 1, 
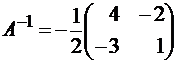. Воспользуемся формулой (3):
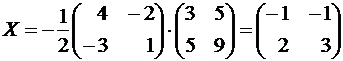
Пример 2. Решить матричное уравнение
.
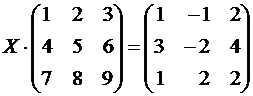Решение.
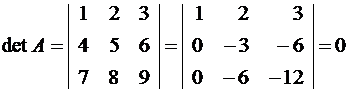(в силу пропорциональности строк), т.е. матрица A – вырожденная, следовательно уравнение решения не имеет.
Пример 3. Решить уравнение
.
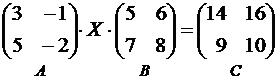Решение. Данное уравнение записываем в виде A∙X∙B = C. Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1∙A∙X∙B∙B-1 = A-1∙C∙B-1. Так как A∙A-1 = B∙B-1 = E и E∙X = X∙E = X, то X = A-1∙C∙B-1.
Находим обратные матрицы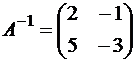 
, 
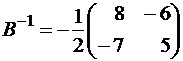, тогда
.
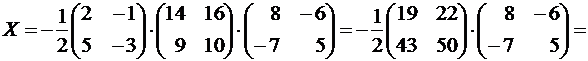
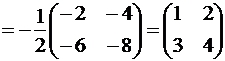Проверка.
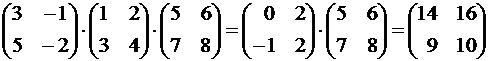
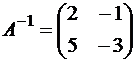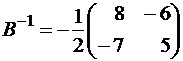, , тогда
.
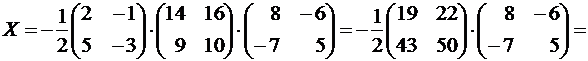
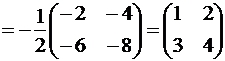Проверка.
Перейти к онлайн решению своей задачи
Классификация решений матричных уравнений
Вариантов записей матричных уравнений может быть достаточно много, однако, все их можно свести к двум видам:- A·X = B
- Y·A = B
Перед изучением материала необходимо иметь представление об операциях над матрицами:
- умножение матриц (
A*B): соответствующие элементы матриц умножаем и складываем: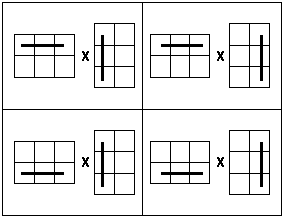
;
- сложение матриц (
C+B): складываются соответствующие элементы матриц C и B
;
- разница (вычитание) матриц (
A-B): из каждого элемента матрицы A вычитается соответствующий элемент матрицы B
;
- умножение матрицы на число (
2*C): число умножается на каждый элемент матрицы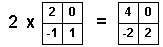
;
Пример 1. Решить матричные уравнения и сделать проверку.
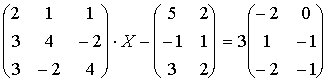
A·X - B = 3C. Его можно записать как A·X = 3C + B. Найдем сумму матриц:
| 3C + B = |
|
Обозначим:
| A = |
|
| B = |
|
Тогда матричное уравнение запишется в виде: A·X = B.
Вычислим определитель матрицы А:
∆ = 2*(4*4 - (-2)*(-2)) - 3*(1*4 - (-2)*1) + 3*(1*(-2) - 4*1) = -12
Определитель матрицы А равен detA=-12
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1: A-1·A·X = A-1·B, тогда получим E·X = A-1·B, или X = A-1·B.
Найдем обратную матрицу A-1.
Транспонированная матрица AT.
| AT = |
|
Алгебраические дополнения
| A1,1 = (-1)1+1 |
|
∆1,1 = (4*4 - (-2)*(-2)) = 12
| A1,2 = (-1)1+2 |
|
∆1,2 = -(1*4 - 1*(-2)) = -6
| A1,3 = (-1)1+3 |
|
∆1,3 = (1*(-2) - 1*4) = -6
| A2,1 = (-1)2+1 |
|
∆2,1 = -(3*4 - (-2)*3) = -18
| A2,2 = (-1)2+2 |
|
∆2,2 = (2*4 - 1*3) = 5
| A2,3 = (-1)2+3 |
|
∆2,3 = -(2*(-2) - 1*3) = 7
| A3,1 = (-1)3+1 |
|
| A3,2 = (-1)3+2 |
|
| A3,3 = (-1)3+3 |
|
Обратная матрица A-1.
| A-1 = 1/12 |
|
| X= 1/12 |
| · |
| = |
|
| X = |
|
Пример 2.
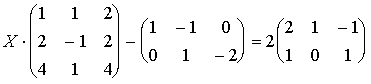
Данное выражение в матричной форме имеет вид: X·A - B = 2C. Преобразуем к виду: X·A = 2C + B или X·A = D, где D = 2C + B
Пример 3.
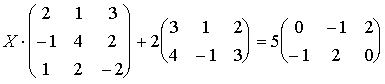
Пример 4.
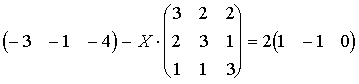
A - X·B = 2C. Сводим его к типу X·B = A + 2C или X·B = D, где D = A + 2C.
| A + 2C = |
|
Обозначим:
| A = |
|
| B = |
|
Тогда матричное уравнение запишется в виде: Y·A = B.
Вычислим определитель матрицы А:
∆ = 3*(3*3 - 1*1) - 2*(2*3 - 1*2) + 1*(2*1 - 3*2) = 12
Определитель матрицы А равен detA=12
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим справа обе части уравнения на A-1: X·A·A-1 = B·A-1, откуда находим, что X = B·A-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT.
| AT = |
|
| A1,1 = (-1)1+1 |
|
| A1,2 = (-1)1+2 |
|
| A1,3 = (-1)1+3 |
|
| A2,1 = (-1)2+1 |
|
| A2,2 = (-1)2+2 |
|
| A2,3 = (-1)2+3 |
|
| A3,1 = (-1)3+1 |
|
| A3,2 = (-1)3+2 |
|
| A3,3 = (-1)3+3 |
|
Обратная матрица A-1.
| A-1 = 1/12 |
|
| X = |
| 1/12 |
| = |
|
| X = |
|
Пример 2.
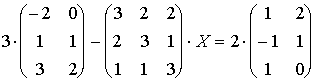
Перейти к онлайн решению своей задачи
Пример №5. Решение матричных уравнений.
Обозначим:
| A = |
|
| B = |
|
| C = |
|
Вычислим определитель матрицы А:
∆ = 3*(-2) - 5*(-1) = -1
Определитель матрицы А равен detA=-1
Так как A невырожденная матрица, то существует обратная матрица A-1. Умножим слева обе части уравнения на A-1:Умножаем обе части этого равенства слева на A-1 и справа на B-1: A-1·A·X·B·B-1 = A-1·C·B-1. Так как A·A-1 = B·B-1 = E и E·X = X·E = X, то X = A-1·C·B-1
Найдем обратную матрицу A-1.
Транспонированная матрица AT.
| AT = |
|
A11 = (-1)1+1·-2 = -2; A12 = (-1)1+2·-1 = 1; A21 = (-1)2+1·5 = -5; A22 = (-1)2+2·3 = 3;
Обратная матрица A-1.
| A-1 = 1/-1 |
|
∆ = 5*8 - 7*6 = -2
Определитель матрицы B равен detB=-2
Найдем обратную матрицу B-1.
Транспонированная матрица BT.
| BT = |
|
A11 = (-1)1+1·8 = 8; A12 = (-1)1+2·6 = -6; A21 = (-1)2+1·7 = -7; A22 = (-1)2+2·5 = 5;
Обратная матрица B-1.
| B-1 = 1/-2 |
|
|
| X = |
|