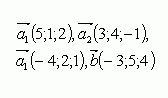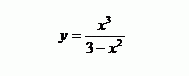Координаты вектора в базисе
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения координат вектора x в новом базисеe(e1, e2, e3) (см. пример решения).
Инструкция. Для онлайн решения необходимо задать количество векторов или размерность заданной матрицы.
Решение. Данная задача состоит из двух частей. Сначала необходимо проверить, образуют ли векторы базис. Векторы образуют базис, если определитель, составленный из координат этих векторов, отличен от нуля, в противном случае вектора не являются базисными и вектор X нельзя разложить по данному базису.
Вычислим определитель матрицы:
| E = |
|
∆ = 2*((-2)*(-4) - (-3)*1) - 3*(1*(-4) - (-3)*3) + 1*(1*1 - (-2)*3) = 14
Определитель матрицы равен ∆ =14
Так как определитель отличен от нуля, то векторы образуют базис, следовательно, вектор X можно разложить по данному базису. Т.е. существуют такие числа α1α2α3, что имеет место равенство:
X = α1ε1 + α2ε2 + α3ε3
Запишем данное равенство в координатной форме:
(7;0;7) = α(2;1;3) + α(3;-2;1) + α(1;-3;-4)
Используя свойства векторов, получим следующее равенство:
(7;0;7) = (2α1;1α1;3α1;) + (3α2;-2α2;1α2;) + (1α3;-3α3;-4α3;)
(7;0;7) = (2α1 + 3α2 + 1α3;1α1 -2α2 -3α3;3α1 + 1α2 -4α3)
По свойству равенства векторов имеем:
2α1 + 3α2 + 1α3 = 7
1α1 -2α2 -3α3 = 0
3α1 + 1α2 -4α3 = 7
Решаем полученную систему уравнений методом Гаусса или методом Крамера.
Ответ:
| X = |
|
X = 2ε1 + ε2
В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.
a1=(1;5;3), a2=(2;1;-1), a3=(4;2;1), a4=(17;13;4),
Пример №2. В системе векторов a1, a2, a3, a4 найти любую подсистему векторов, которые образуют базис, разложить векторы по базису, перейти к другому базису, найти коэффициенты разложения векторов во втором базисе; в обоих случаях определить обратные матрицы, соответствующие векторам базиса. Правильность вычисления в каждом случае проверить с помощью умножения вектора слева на матрицу, обратную матрице вектора базиса.a1=(1;5;3), a2=(2;1;-1), a3=(4;2;1), a4=(17;13;4).