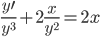Минимум функции методом наискорейшего спуска
Назначение сервиса. Онлайн-калькулятор используется для нахождения минимума функции методом наискорейшего спуска или методом Коши. Решение оформляется в формате Word.Правила ввода функции
- Все переменные выражаются через x1,x2
В методе наискорейшего спуска в качестве направления поиска выбирается вектор, направление которого противоположно направлению вектора градиента функции ▽f(x). Из математического анализа известно, что вектор grad f(x)=▽f(x) характеризует направление наиболее быстрого возрастания функции (см. градиент функции). Поэтому вектор -grad f (X) = -▽f(X) называется антиградиентом и является направлением наиболее быстрого ее убывания. Рекуррентное соотношение, с помощью которого реализуется метод наискорейшего спуска, имеет вид Xk+1=Xk - λk▽f(xk), k = 0,1,...,
где λk>0 - величина шага. В зависимости от выбора величины шага можно получить различные варианты градиентного метода. Если в процессе оптимизации величина шага λ фиксирована, то метод носит название градиентного метода с дискретным шагом. Процесс оптимизации на первых итерациях можно значительно ускорить, если λk выбирать из условия λk=min f(Xk + λSk).
Для определения λk используется любой метод одномерной оптимизации. В этом случае метод называется методом наискорейшего спуска. Как правило, в общем случае недостаточно одного шага для достижения минимума функции, процесс повторяют до тех пор, пока последующие вычисления позволяют улучшать результат.
Если пространство очень вытянуто по некоторым переменным, то образуется “овраг”. Поиск может замедлиться и идти зигзагами поперек дна “оврага”. Иногда решение невозможно получить за приемлемое время.
Еще одним недостатком метода может быть критерий остановки |▽f(Xk)|<εk, так как этому условию удовлетворяет и седловая точка, а не только оптимум.
Пример 1. Начиная из точки xk=(-2, 3) определите точку xk+1 методом наискорейшего спуска для минимизации функции f(x)=3x12+x22-x1x2-4x1 → min.
В качестве направления поиска выберем вектор градиент в текущей точке
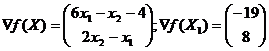
Проверим критерий остановки |▽f(X1)|<ε. Имеем |▽f(X1)|=20.1>0.1.
Вычислим значение функции в начальной точке f(X1) = 35. Сделаем
шаг вдоль направления антиградиента
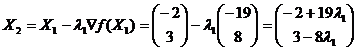
f(X2) = 3(-2 + 19λ1)2 + (3-8λ1)2 - (-2 + 19λ1)(3-8λ1) - 4(-2 + 19λ1)
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции
f’(X2) = 6(-2 + 19λ1) 19 + 2(3-8λ1)( -8) – (73 - 304 λ1) – 4*19
или f’(X2) = 2598 λ1 – 425 = 0.
Получим шаг λ1 = 0.164
Выполнение этого шага приведет в точку
в которой значение градиента |▽f(X2)|=2.02>0.1, значение функции f(X2) = 0.23. Точность не достигнута, из точки делаем шаг вдоль направления антиградиента ▽f(X2).
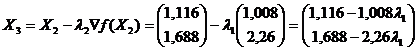
f’(X2) = 11,76 – 6,12λ1 = 0
Получаем λ1 = 0.52
Пример №2. Найти минимум целевой функции методом Коши с точностью ε=0.1.
f(x) = 8x12+4x1x2+522.
Итерация №1. В качестве направления поиска выберем вектор градиент в текущей точке:
| ▽f(X) = |
|
Значение градиента в точке X1:
| ▽f(X1) = |
|
Проверим критерий остановки:
|▽f(X1)| < ε
Имеем:
|▽f(X1)| = 53.85>0.1
Вычислим значение функции в начальной точке f(X1) = 125. Сделаем шаг вдоль направления антиградиента
| X2 = X1 - λ1▽f(X1) = |
| - λ1 |
| = |
|
Вычислим значение функции в новой точке.
f(X2) = 8*(4-52*λ1)2+4*(4-52*λ1)*(-3+14*λ1)+5*(-3+14*λ1)2
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(X)=0):
-2900+39400*λ1 = 0
Получим шаг: λ1 = 0.0736
Выполнение этого шага приведет в точку:
| X2 = |
| - 0.0736 |
| = |
|
Итерация №2. Значение градиента в точке X1:
| ▽f(X1) = |
|
Проверим критерий остановки:
|▽f(X2)| < ε
Имеем:
|▽f(X1)| = 19.6812695251094>0.1
Вычислим значение функции в начальной точке f(X2) = 18.273. Сделаем шаг вдоль направления антиградиента
| X3 = X2 - λ2▽f(X2) = |
| - λ2 |
| = |
|
f(X3) = 8*(0.17260+5.11640*λ2)2+4*(0.17260+5.11640*λ2)*(-1.9695+19.0046*λ2)+5*(-1.9695+19.0046*λ2)2
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(X)=0):
-387.35+4808.47*λ2 = 0
Получим шаг: λ2 = 0.08056
Выполнение этого шага приведет в точку:
| X3 = |
| - 0.08056 |
| = |
|
Пример №3. Найти максимум функции f(x) методом Коши (методом наискорейшего спуска).
f(x) = 4x1 + 2x2 – x12 – x22 + 5 → max
x0=[4;5]
Решение. Сведем поиск максимального значения на поиск минимального значения функции. Для этого умножим функцию на (-1).
f(x) = -4x1 - 2x2 + x12 + x22 - 5 → min
Итерация №1. В качестве направления поиска выберем вектор градиент в текущей точке:
| ▽f(X) = |
|
Значение градиента в точке X1:
| ▽f(X1) = |
|
Проверим критерий остановки:
|▽f(X1)| < ε
Имеем:
|▽f(X1)| = 8.94427190999916>0.1
Вычислим значение функции в начальной точке f(X1) = 10. Сделаем шаг вдоль направления антиградиента
| X2 = X1 - λ 1▽f(X1) = |
| - λ 1 |
| = |
|
Вычислим значение функции в новой точке.
f(X2) = -4*(4-4*λ1)-2*(5-8*λ1)+(4-4*λ1)2+(5-8*λ1)2-5
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f'(X)=0):
-80+160*λ1 = 0
Получим шаг: λ1 = 0.5
Выполнение этого шага приведет в точку:
| X2 = |
| - 0.5 |
| = |
|
Итерация №2. Значение градиента в точке X1:
| ▽f(X1) = |
|
Проверим критерий остановки: |▽f(X2)|<ε. Имеем: |▽f(X1)| = 0<0.1.
Ответ: x1=2; x2=1. F(X) = 10.