Минимум функции методом Ньютона
Назначение сервиса. Онлайн-калькулятор используется для нахождения минимума функции двух переменных методом Ньютона. Решение оформляется в формате Word. Чтобы найти минимум функции одной переменной, используйте этот калькулятор.- Все переменные выражаются через x1,x2
- Все математические операции выражаются через общепринятые символы (
+,-,*,/,^). Например, x12+x1x2, записываем какx1^2+x1*x2.
Пусть функция f(x) дважды непрерывно дифференцируема и Xk - некоторая точка пространства поиска. Из курса математического анализа известно, что дважды непрерывно дифференцируемую функцию в достаточно малой окрестности точки Xk можно разложить в ряд Тейлора, отбрасывая члены третьего и более высоких порядков:
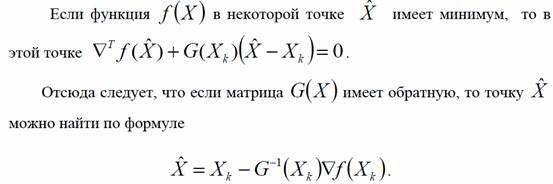
Повторяя эту процедуру, получим рекуррентную формулу метода Ньютона:
В задачах поиска минимума произвольной квадратичной функции с положительно определенной матрицей вторых производных, метод Ньютона дает решение за одну итерацию независимо от выбора начальной точки. В общем случае метод Ньютона может расходиться, если начальное приближение находится вдали от точки минимума. Сходимость метода Ньютона можно гарантировать только в тех случаях, когда начальное приближение находится в достаточно малой окрестности точки минимума и матрица Гессе положительно определена и хорошо обусловлена. Поэтому на практике этот метод обычно используется в сочетании с одним из методов, быстро сходящимся вдали от точки минимума.
Пример 1. Начиная из точки xk=(10;10), определите точку xk+1 методом Ньютона для минимизации функции 8x12+4x1x2+5x22.
В качестве направления поиска выберем ньютоновское направление, для этого вычислим градиент:
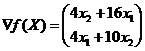
Значение градиента в точке X1:
![]()
Проверим критерий остановки:
|∆f(X1)| < ε
Имеем:
|∆f(X1)| = 20*sqrt(149)>ε
Сделаем шаг вдоль ньютоновского направления:
![]()
Найдем матрицу Гессе и обратный гессиан.
![]()
![]()
![]()
Матрица Гессе: ![]()
Обратный гессиан:
detG = 16•10 - 4•4 = 144
![]()
Получим:
![]()
В этой точке |∆f(X1)| = 0 и матрица Гессе положительно определена, следовательно
![]()
Пример 2.
В качестве направления поиска выберем ньютоновское направление, для этого вычислим градиент:
| ▽f(X) = |
|
Значение градиента в точке X1:
| ▽f(X1) = |
|
Имеем: |▽f(X1)| = 5*sqrt(17)>0.1
Сделаем шаг вдоль ньютоновского направления:
X2 = X1 - G-1▽f(X1)
Найдем матрицу Гессе и обратный гессиан.
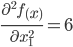
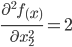
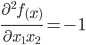
Матрица Гессе:
| G = |
|
Обратный гессиан:
detG = 6•(-1) - 2•2 = 11
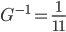 |
|
Получим:
| X2 = |
| 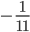 |
|
| = |
|
В этой точке |▽f(X1)| = 0 и матрица Гессе положительно определена, следовательно
| Xmin = |
|
Итерация №2.
В качестве направления поиска выберем ньютоновское направление, для этого вычислим градиент:
| ▽ f(X) = |
|
Значение градиента в точке X1:
| ▽ f(X1) = |
|
Имеем: |▽f(X1)| = 0<0.1