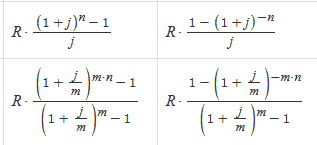Формула трапеции
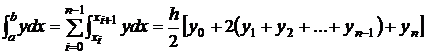
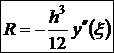 или
или 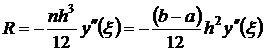
Назначение сервиса. Сервис предназначен для онлайн вычисления определенного интеграла по формуле трапеции.
Инструкция. Введите подынтегральную функцию f(x), нажмите Решить. Полученное решение сохраняется в файле Word. Также создается шаблон решения в Excel.
Правила ввода функции
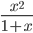 ≡ x^2/(1+x)
≡ x^2/(1+x)
cos2(2x+π) ≡ (cos(2*x+pi))^2
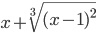 ≡ x+(x-1)^(2/3)
≡ x+(x-1)^(2/3)
Вывод формулы трапеции
Пусть n=1 (две точки). Тогда из формулы (3) получаем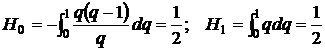
Это известная формула трапеций. Остаточный член равен

Получим формулу для R. Пусть известно, что y∈C(2) [a,b]. Запишем R в виде
R=R(h)
Дифференцируя эту формулу по h два раза, получим
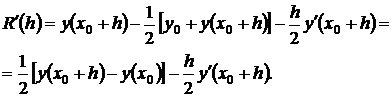
Отсюда, интегрируя по h и используя теорему о среднем, последовательно выводим
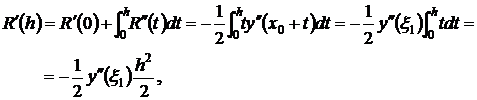
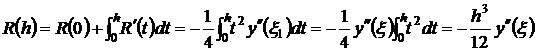
Таким образом,
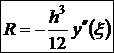 . (6)
. (6)
Получим теперь формулу трапеций для
Пусть задана сетка {xi}, где xi=a+ih, i=0,..,n. Тогда интеграл
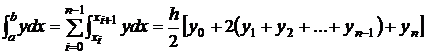 , (7)
, (7)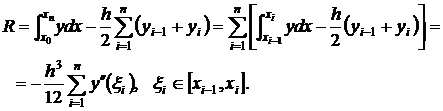 (8)
(8)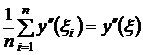 .
.
Следовательно, из (8) получим
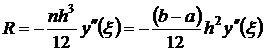 . (9)
. (9)
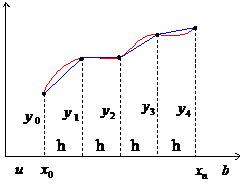
Геометрически формула (7) получается, если график функции y=f(x) заменить ломаной.
Из формул (6) и (9) видно, что если y″ > 0, то формула трапеции (5), (7) даст значение интеграла с избытком, если y″<0, то – с недостатком.
Замечание. Если сетка неравномерная, то вместо формулы (7) будем иметь:
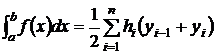 .
.
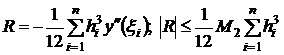 .
.
Пример №2. Используя обобщенные формулы трапеций и Симпсона вычислить определенные интегралы с заданной точностью. Проверку достижения требуемой точности проводить по правилу Рунге.
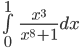
Формула трапеций:
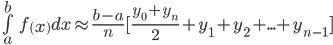
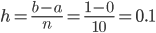
| i | xi | yi |
| 0 | 0 | 0 |
| 1 | 0.1 | 0.001 |
| 2 | 0.2 | 0.008 |
| 3 | 0.3 | 0.027 |
| 4 | 0.4 | 0.06396 |
| 5 | 0.5 | 0.1245 |
| 6 | 0.6 | 0.2124 |
| 7 | 0.7 | 0.3243 |
| 8 | 0.8 | 0.4384 |
| 9 | 0.9 | 0.5096 |
| 10 | 1 | 0.5 |
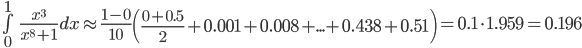
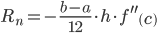
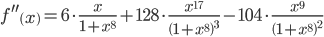
Найдем максимальное значение второй производной функции на интервале [0;1].
y = 6*x/(1+x^8)+128*x^17/((1+x^8)^3)-104*x^9/((1+x^8)^2)
[0;1]
Находим первую производную функции:
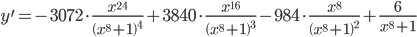
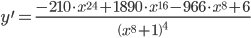
Приравниваем ее к нулю:
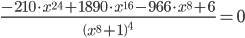
Поскольку глобальных экстремумов нет, то находим стационарные точки. Вычисляем значения функции на концах отрезка:
f(0) = 0; f(1) = -7
fmin = -7, fmax = 0
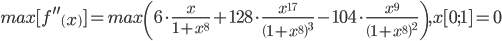
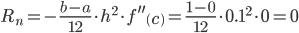
Таким образом, I = 0.196 ± 0