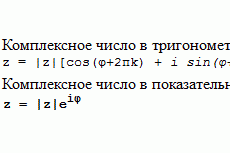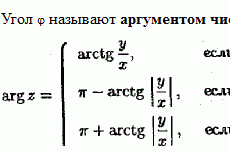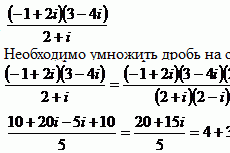Метод сопряженных градиентов
Назначение сервиса. Онлайн-калькулятор предназначен для нахождения минимума функции методом сопряженных градиентов. Метод Флетчера-Ривза и метод сопряженных градиентов – это разные методы, хотя второй и является разновидностью первого. Флетчер и Ривз расширили предшествующий метод на случай произвольных функций. В применении к квадратичным функциям он становится равносильным методу сопряженных градиентов. Также реализован вариант Миля-Кентрелла.
Решение оформляется в формате Word.
Правила ввода функций:
- Все переменные выражаются через x1,x2
x12+x1x2, записываем как x1^2+x1*x2
Метод сопряженных градиентов формирует направления поиска, в большей мере соответствующие геометрии минимизируемой функции.
Определение. Два n-мерных вектора х и у называют сопряженными по отношению к матрице A (или A-сопряженными), если скалярное произведение (x, Aу) = 0. Здесь A - симметрическая положительно определенная матрица размером n х n.
Схема алгоритма метода сопряженных градиентов
Положить k=0.Ш. 1 Пусть x0 - начальная точка; g0=∇f(x0)=Ax0+b,
d0=-g0; k=0.
Ш. 2 Определить xk+1=xk+λkdk, где
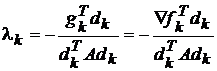.Затем dk+1=-gk+1+βkdk,
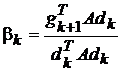,βk находится из условия dk+1Adk=0 (сопряжены относительно матрицы A).
Ш. 3 Положить k=k+1 → Ш. 2.
Критерий останова одномерного поиска вдоль каждого из направлений dk записывается в виде: ∇f(xk+1)dk=0.
Значения βi(i=1,k-1) выбираются таким образом, чтобы направление dk было A-сопряжено со всеми построенными ранее направлениями.
Метод Флетчера-Ривса
Стратегия метода Флетчера-Ривса состоит в построении последовательности точек {xk}, k=0, 1, 2, ... таких, что f(xk+1) < f(xk), k=0, 1, 2, ...Точки последовательности {xk} вычисляются по правилу:
xk+1=xk-tkdk, k = 0, 1, 2,…
dk = ▽f(xk) + bk-1▽f(xk-1)
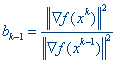
Величина шага выбирается из условия минимума функции f(х) по t в направлении движения, т. е. в результате решения задачи одномерной минимизации:
f(xk-tkdk) → min (tk>0)
В случае квадратичной функции f(x)= (х, Нх) + (b, х) + а направления dk, dk-1 будут H-сопряженными, т.е. (dk, Hdk-1)=0
При этом в точках последовательности {xk} градиенты функции f(x) взаимно перпендикулярны, т.е. (▽f(xk+1),▽f(xk))=0, k =0, 1, 2…
При минимизации неквадратичных функций метод Флетчера-Ривса не является конечным. Для неквадратичных функций используется следующая модификация метод Флетчера-Ривса (метод Полака-Рибьера), когда величина bk-1 вычисляется следующим образом:
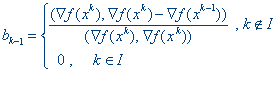
Здесь I- множество индексов: I = {0, n, 2n, 3n, ...}, т. е. метод Полака-Рибьера предусматривает использование итерации наискорейшего градиентного спуска через каждые n шагов с заменой x0 на xn+1.
Построение последовательности{xk} заканчивается в точке, для которой |▽f(xk)|<ε.
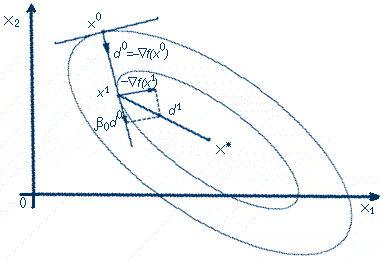
Геометрический смысл метода сопряженных градиентов состоит в следующем. Из заданной начальной точки x0 осуществляется спуск в направлении d0 = ▽f(x0).В точке x1 определяется вектор-градиент ▽f(x1).Поскольку x1 является точкой минимума функции в направлении d0, то▽f(x1) ортогонален вектору d0. Затем отыскивается вектор d1, H-сопряженный к d0. Далее отыскивается минимум функции вдоль направления d1 и т. д.
Алгоритм метода Флетчера-Ривса
Начальный этап.Задать x0, ε > 0.
Найти градиент функции в произвольной точке
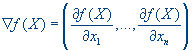
k=0.
Основной этап
Шаг 1. Вычислить ▽f(xk)
Шаг 2. Проверить выполнение критерия останова |▽f(xk)|< ε
а) если критерий выполнен, расчет окончен,x*=xk
б) если критерий не выполнен, то перейти к шагу 3, если k=0, иначе к шагу 4.
Шаг 3. Определить d0= ▽f(x0)
Шаг 4. Определить
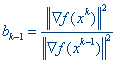или в случае неквадратичной функции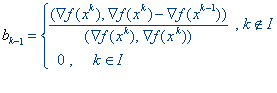 
Шаг 5. Определить dk = ▽f(xk) + bk-1▽f(xk-1)
Шаг 6. Вычислить величину шага tk из условия f(xk - tkdk) → min (tk>0)
Шаг 7. Вычислить xk+1=xk-tkdk
Шаг 8. Положить k= k +1 и перейти к шагу 1.
Сходимость метода
Теорема 1. Если квадратичная функцияf(x) = (х, Нх) + (b, х) + а с неотрицательно определенной матрицей Н достигает своего минимального значения на Rn, то метод Флетчера-Ривса обеспечивает отыскание точки минимума не более чем за n шагов.
Теорема 2. Пусть функция f(x) дифференцируема и ограничена снизу на Rm, а ее градиент удовлетворяет условию Липшица
. Тогда при произвольной начальной точке 
для метода Полака-Рибьера имеем 
Теорема 2 гарантирует сходимость последовательности {xk} к стационарной точке x*, где ▽f(x*)=0. Поэтому найденная точка x* нуждается в дополнительном исследовании для ее классификации. Метод Полака-Рибьера гарантирует сходимость последовательности {xk} к точке минимума только для сильно выпуклых функций.
Оценка скорости сходимости получена только для сильно выпуклых функций, в этом случае последовательность {xk} сходится к точке минимума функции f(x) со скоростью: |xk+n – x*| ≤ C|xk – x*|, k = {0, n, 2, …}
Пример. Найти минимум функции методом сопряженных градиентов: f(X) = 2x12+2x22+2x1x2+20x1+10x2+10.
Решение. В качестве направления поиска выберем вектор градиент в текущей точке:
| ▽ f(X) = |
|
Итерация №0.
| ▽ f(X0) = |
|
Проверим критерий остановки: |▽f(X0)| < ε
Вычислим значение функции в начальной точке f(X0) = 10.
Сделаем шаг вдоль направления антиградиента.
| X1 = X0 - t0▽ f(X0) = |
| - t0 |
| = |
|
f(X1) = 2*(-20.0*t0)2+2*(-10.0*t0)2+2*(-20.0*t0)*(-10.0*t0)+20*(-20.0*t0)+10*(-10.0*t0)+10 → min
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f '(x1)=0):
2800*t1-500 = 0
Получим шаг: t0 = 0.1786
Выполнение этого шага приведет в точку:
| X0 = |
| - 0.1786 |
| = |
|
Итерация №1.
| ▽ f(X1) = |
|
Проверим критерий остановки: |▽f(X1)| < ε
Вычислим значение функции в новой точке f(X1) = -34.643.
X2 = X1 - t1d1
d1 = ▽f(X1) + b0▽f(X0)
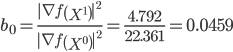
| d1 = |
| + 0.0459 |
| = |
|
Сделаем шаг вдоль направления антиградиента.
| X2 = X1 - t1▽ f(X1) = |
| - t1 |
| = |
|
f(X2) = 2*(-3.0612*t1-3.5714)2+2*(3.8265*t1-1.7857)2+2*(-3.0612*t1-3.5714)*(3.8265*t1-1.7857)+20*(-3.0612*t1-3.5714)+10*(3.8265*t1-1.7857)+10 → min
Найдем такой шаг, чтобы целевая функция достигала минимума вдоль этого направления. Из необходимого условия существования экстремума функции (f '(x2)=0):
49.19825*t2-22.95918 = 0
Получим шаг: t0 = 0.4667
Выполнение этого шага приведет в точку:
| X0 = |
| - 0.4667 |
| = |
|
Итерация №2.
| ▽ f(X2) = |
|
Проверим критерий остановки: |▽f(X2)| < ε
Вычислим значение функции в новой точке f(X2) = -40.
Анализ решения. Найдем матрицу Гессе функции f(X) = 2x12+2x22+2x1x2+20x1+10x2+10.
| H = |
|
